计及物资装载率优化的电表配送车辆路径规划方法及系统与流程

1.本发明涉及物流调度的技术领域，尤其涉及计及物资装载率优化的电表配送车辆路径规划方法及系统。


背景技术：

2.随着数字经济的持续发展，实体经济与数字经济相互融合，电网的智能化水平显著提高。构建智能电网和智慧电力已逐渐成为当前电网企业的主要发展趋势。物资调度作为电网企业构建智慧物流的重要组成部分，需要进行数字化，经济化改进，构建新型精细化供应系统以满足智慧物流的仓储物资的配送需求。电网物资配送涉及到一个计及复杂环境约束条件的多目标车辆路径规划问题(vehicleroutingproblem，vrp)，而目前今针对多收货点的同时考虑运输车辆差异、时间窗、运输成本、客户满意度等问题的技术少之又少，在研究上存在不足，为此本发明人基于相关理论研究，结合改进白鲸算法建立多维约束条件建立多目标优化的电网物资配送调度模型，提供一种计及物资装载率优化的电表配送车辆路径规划方法。
3.电网配送较传统的货物配送调度方案不同，其具有配送范围广、配送货物数量多且种类复杂、签约承运车型异构、运输距离等复杂约束，因此跨区域的电网配送运输的核心问题是一个涉及多维复杂环境条件约束的多目标车辆路径规划问题。
4.为提高省计量中心智能电表配送效率，实现多层电表轮换配送业务中的车辆订单配送选择最优化，本发明是针对大规模电表轮换配送要求，致力于做到车辆固定成本最低、配送成本最小、人工成本最低、电表轮换储存成本最低，得到最优的电网企业批量轮转物资调配求解方案。


技术实现要素：

5.本部分的目的在于概述本发明的实施例的一些方面以及简要介绍一些较佳实施例。在本部分以及本技术的说明书摘要和发明名称中可能会做些简化或省略以避免使本部分、说明书摘要和发明名称的目的模糊，而这种简化或省略不能用于限制本发明的范围。
6.鉴于上述现有针对在电网物资配送中多收货点同时考虑运输车辆差异、时间窗、运输成本、客户满意度等问题的技术极少，以及在研究上存在不足的问题，提出了本发明。
7.因此，本发明目的是提供计及物资装载率优化的电表配送车辆路径规划方法及系统。
8.为解决上述技术问题，本发明提供如下技术方案：
9.作为本发明所述的计及物资装载率优化的电表配送车辆路径规划方法，其中：建立大规模电表轮换配送车辆调度模型，根据每个订单编号确定配送电表种类及相应的收货点，确定每个订单发货地点；
10.设定白鲸优化算法改进过程中的个体编码和解码格式，通过立方混沌映射构造具有高遍历性的映射初始订单种群；
11.根据平衡因子判断所述白鲸优化算法是否处于探索阶段或开发阶段，并建立一种基于种群分级的精英扰动机制提高白鲸优化算法后期的收敛精度和全局搜索能力；
12.检查迭代次数是否满足要求。
13.作为本发明所述的计及物资装载率优化的电表配送车辆路径规划方法，其中：建立大规模电表轮换配送车辆调度模型包括，
14.设定模型条件，再构建多阶段配送优化模型并满足相应的约束条件；
15.其中，设定模型条件如下：
16.在一层配送网络中车辆完成配送后返回计量中心，在二层配送网络中车辆完成配送后返回各自的供电局；
17.配送车辆仅考虑载重限制；
18.在配送过程中，当计量中心-供电局的配送任务完成后，供电局进行下一层配送任务；
19.其中，构建多阶段配送优化模型如下：
20.计算第一层和第二层配送网络的车辆固定成本、计算第一层和第二层配送网络的配送成本、计算人员作业成本、计算智能电表装置的存贮成本、最小化三项成本总和得到多阶段配送优化模型以及全部满足一定的约束条件。
21.作为本发明所述的计及物资装载率优化的电表配送车辆路径规划方法，其中：所述一定的约束条件包括供电所的需求连续性约束、供电局的需求连续性约束、第一层配送网络中的车辆的载重约束、第二层配送网络中的车辆的载重约束、第一层配送网络中的计量中心的车数约束、第二层配送网络中的任意供电局的车数约束、保证第一层配送网络中的车辆返回计量中心、保证第二层配送网络中的车辆返回供电局、消除第一层配送网络中的子回路、消除第二层配送网络中的子回路、保证第一层配送网络中的车辆进入供电局后必须离开、保证第二层配送网络中的车辆进入供电所后必须离开、第一层配送网络中的车辆的最远距离约束、第二层配送网络中的车辆的最远距离约束、第一层配送网络中的计量中心最大服务水平约束、第二层配送网络中的供电局的最大服务水平约束、供电局的最大存贮能力约束以及供电所的最大存贮能力约束。
22.作为本发明所述的计及物资装载率优化的电表配送车辆路径规划方法，其中：通过立方混沌映射构造具有高遍历性的映射初始订单种群包括，
23.立方映射的公式如下：
24.c(o+1)＝4c(o)
3-3y(o)
[0025]-1＜c(0)＜1,c(o)≠0o＝0,1,2,...
[0026]
其中，c为混沌变量，设定初始白鲸种群由nop个d维订单组成，白鲸种群数量nop映射为订单配送方案数量，白鲸种群的维度d映射为订单个数，
[0027]
生成之间的随机数作为每个订单配送方案中的第一维度的位置，根据立方映射的公式通过迭代的方法生成种群个体中每一维度的后续d-1个个体，将立方映射产生的变量值映射到白鲸种群个体中，具体公式如下：
[0028]
xc＝x
initial
·
(c+1)/2
[0029]
其中，xc为映射后的初始订单种群，x
initial
为初始订单种群。
[0030]
作为本发明所述的计及物资装载率优化的电表配送车辆路径规划方法，其中：通
过立方混沌映射构造具有高遍历性的映射初始订单种群包括，
[0031]
判断映射后的初始订单方案种群混沌解，生成初始可行订单种群解；
[0032]
若车辆所承运的订单不满足大规模电表轮换配送车辆调度模型中的约束时，则此时映射后的初始订单方案种群混沌解为不可接受解；
[0033]
若车辆所承运的订单满足大规模电表轮换配送车辆调度模型中的约束时，则此时初始混沌解为可接受解即生成初始可行订单种群解。
[0034]
作为本发明所述的计及物资装载率优化的电表配送车辆路径规划方法，其中：根据平衡因子判断所述白鲸优化算法是否处于探索阶段或开发阶段包括，
[0035]
若平衡因子大于0.5，则白鲸优化算法处于探索阶段，需通过奇偶数的选择更新订单在种群中的位置增加全局搜索能力；
[0036]
若平衡因子小于等于0.5，则白鲸优化算法处于开发阶段，需通过引入鲸鱼优化算法的包围猎物机制增加算法的局部搜索能力。
[0037]
作为本发明所述的计及物资装载率优化的电表配送车辆路径规划方法，其中：建立一种基于种群分级的精英扰动机制包括，根据目标函数值将订单种群分为精英种群与劣势种群，具体公式如下：
[0038][0039]
其中，f
it
为第i个订单方案所得到的适应度函数值，为平均适应度函数值；
[0040]
若第i个订单方案所得到的适应度函数值小于平均适应度函数值，则视为精英个体；
[0041]
若第i个订单方案所得到的适应度函数值大于平均适应度函数值，则视为劣势个体；
[0042]
在精英种群中实行黄金正弦机制，提高算法的收敛速度以及最优位置的局部搜索能力，具体公式如下：
[0043][0044][0045]
其中，为第t代中第i个订单配送方案，r1为[0，2π]的随机数，决定精英个体的移动距离，r2为[0，π]的随机数，决定精英个体的移动方向，x1和x2为黄金分割系数，τ为黄金分割数。
[0046]
在劣质种群中通过白鲸种群的鲸落机制，使劣势种群跳出当前的搜索空间并找到更好的空间位置；
[0047]
在劣势种群中，若白鲸个体的勘测概率小于鲸落概率，则执行种群淘汰，若白鲸个体的勘测概率大于鲸落概率，则执行自由扰动；
[0048]
种群淘汰公式如下：
[0049]
[0050][0051]
wf＝0.1-0.05t/t
max
[0052]
自由扰动公式如下：
[0053][0054]
其中，为第t代中第i个订单配送方案，为第t代中第r个订单配送方案，x
step
为白鲸坠落的步长，wf为鲸鱼坠落的概率，c2为阶跃因子，ub和lb分别是订单的上限和下限，为当前种群中任意的订单配送方案。
[0055]
第二方面，本发明实施例提供了计及物资装载率优化的电表配送车辆路径规划系统，包括，
[0056]
模型搭建模块，用于建立大规模电表轮换配送车辆调度模型，根据每个订单编号确定配送电表种类及相应的收货点，确定每个订单发货地点；
[0057]
算法改进模块，用于改进白鲸优化算法，提高白鲸优化算法在物流调度配送中的寻优能力；
[0058]
输出模块，用于根据平衡因子判断所述白鲸优化算法是否处于探索阶段或开发阶段，同时检查迭代次数是否满足要求。
[0059]
第三方面，本发明实施例提供了一种计算设备，包括：
[0060]
存储器和处理器；
[0061]
所述存储器用于存储计算机可执行指令，所述处理器用于执行所述计算机可执行指令，该计算机可执行指令被处理器执行时实现权利要求1至7任意一项所述计及物资装载率优化的电表配送车辆路径规划方法的步骤。
[0062]
第四方面，本发明实施例提供了一种计算机可读存储介质，其存储有计算机可执行指令，该计算机可执行指令被处理器执行时实现权利要求1至7任意一项所述计及物资装载率优化的电表配送车辆路径规划方法的步骤。
[0063]
本发明的有益效果：本发明针对大规模电表轮换配送要求，可有效降低车辆固定成本、配送成本、人工成本以及电表轮换储存成本，实现最优电网企业批量轮转物资调配求解方案。
附图说明
[0064]
为了更清楚地说明本发明实施例的技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其它的附图。其中：
[0065]
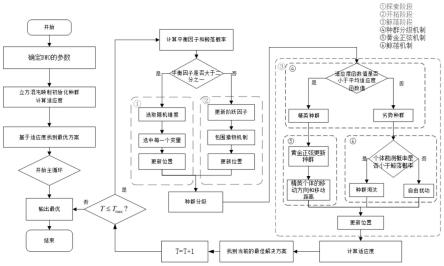
图1为本发明计及物资装载率优化的电表配送车辆路径规划方法及系统的算法流程图。
[0066]
图2为本发明计及物资装载率优化的电表配送车辆路径规划方法及系统的编码-解码示意图。
[0067]
图3为本发明计及物资装载率优化的电表配送车辆路径规划方法及系统的订单初
始化示意图。
[0068]
图4为本发明计及物资装载率优化的电表配送车辆路径规划方法所述的一种基于种群分级的精英扰动机制图。
具体实施方式
[0069]
为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合说明书附图对本发明的具体实施方式做详细的说明。
[0070]
在下面的描述中阐述了很多具体细节以便于充分理解本发明，但是本发明还可以采用其他不同于在此描述的其它方式来实施，本领域技术人员可以在不违背本发明内涵的情况下做类似推广，因此本发明不受下面公开的具体实施例的限制。
[0071]
其次，此处所称的“一个实施例”或“实施例”是指可包含于本发明至少一个实现方式中的特定特征、结构或特性。在本说明书中不同地方出现的“在一个实施例中”并非均指同一个实施例，也不是单独的或选择性的与其他实施例互相排斥的实施例。
[0072]
再其次，本发明结合示意图进行详细描述，在详述本发明实施例时，为便于说明，表示器件结构的剖面图会不依一般比例作局部放大，而且所述示意图只是示例，其在此不应限制本发明保护的范围。此外，在实际制作中应包含长度、宽度及深度的三维空间尺寸。
[0073]
实施例1
[0074]
参照图1～图4，提供了计及物资装载率优化的电表配送车辆路径规划方法及系统，包括：
[0075]
如图1所示，本发明的流程具体如下：
[0076]
s1：建立大规模电表轮换配送车辆调度模型，根据每个订单编号确定配送电表种类及相应的收货点，确定每个订单发货地点。应说明的是：
[0077]
首先设定模型条件，再构建多阶段配送优化模型并满足相应的约束条件。
[0078]
其中，设定模型条件如下：
[0079]
在一层配送网络中车辆完成配送后返回计量中心，在二层配送网络中车辆完成配送后返回各自的供电局。
[0080]
配送车辆仅考虑载重限制。
[0081]
在配送过程中，当计量中心-供电局的配送任务完成后，供电局进行下一层配送任务。
[0082]
其中，构建多阶段配送优化模型如下：
[0083]
计算第一层和第二层配送网络的车辆固定成本，具体公式如下：
[0084][0085]
其中，fc为计量中心出动单位车次固定成本，为车辆kc的配送人工成本，若车辆kc被使用时，则若车辆kc未被使用时，则fi为供电局i出动单位车次固定成本，若车辆ki被使用时，则若车辆ki未被使用时，则r
ki
＝0，为车辆ki的配送人工成本，vc为计量中心c车辆集合，vc＝{1，2，
…
，kc，
…
，kc}。
[0086]
计算第一层和第二层配送网络的配送成本，具体公式如下：
[0087][0088]
其中，cd为单位距离配送成本，d
ci
为计量中心到供电局i的距离，d
im
为供电局i到供电所m的距离，d
mn
为供电所m到供电所n的距离。
[0089]
若车辆kc从计量中心c到供电局i时车辆kc未从计量中心c到供电局i时
[0090]
若车辆kc从供电局i到供电局j时车辆kc未从供电局i到供电局j时
[0091]
若车辆ki从供电局i到供电局n时车辆ki未从供电局i到供电局n时
[0092]
计算人员作业成本，具体公式如下：
[0093][0094]
其中，为车辆kc的速度。
[0095]
计算智能电表装置的存贮成本，具体公式如下：
[0096][0097]
其中，λc为周转箱规格，λ
p
为周转垛规格，s(m，m
p
)为供电所m在补货前的物资m
p
的库存量，q(m，m
p
)为供电所m对物资m
p
的需求，i(m，m
p
)为供电所m对物资m
p
的消耗，w
p
为单位时间内周转垛的存贮成本。
[0098]
最小化三项成本总和得到多阶段配送优化模型的目标函数如下：
[0099]
min c＝c
vehicle
+c
transport
+c
stock
+c
pay
[0100]
满足以下约束条件：
[0101]
供电所的需求连续性约束，具体公式如下：
[0102][0103]
其中，为车辆ki给供电所m配送的物资m
p
的数量。
[0104]
供电局的需求连续性约束，具体公式如下：
[0105][0106]
其中，为车辆kc给供电所m配送的物资m
p
的数量。
[0107]
第一层配送网络中的车辆的载重约束，具体公式如下：
[0108]
[0109]
其中，为车辆kc负责的供电局集合，
[0110]
第二层配送网络中的车辆的载重约束，具体公式如下：
[0111][0112]
其中，为车辆ki负责的供电所集合，
[0113]
第一层配送网络中的计量中心的车数约束，具体公式如下：
[0114][0115]
第二层配送网络中的任意供电局的车数约束，具体公式如下：
[0116][0117]
保证第一层配送网络中的车辆返回计量中心，具体公式如下：
[0118][0119]
保证第二层配送网络中的车辆返回供电局，具体公式如下：
[0120][0121]
消除第一层配送网络中的子回路，具体公式如下：
[0122][0123]
消除第二层配送网络中的子回路，具体公式如下：
[0124][0125]
保证第一层配送网络中的车辆进入供电局后必须离开，具体公式如下：
[0126][0127]
保证第二层配送网络中的车辆进入供电所后必须离开，具体公式如下：
[0128][0129]
第一层配送网络中的车辆的最远距离约束，具体公式如下：
[0130][0131]
第二层配送网络中的车辆的最远距离约束，具体公式如下：
[0132][0133]
第一层配送网络中的计量中心最大服务水平约束，具体公式如下：
[0134][0135]
第二层配送网络中的供电局的最大服务水平约束，具体公式如下：
[0136]
[0137]
供电局的最大存贮能力约束，具体公式如下：
[0138][0139]
供电所的最大存贮能力约束，具体公式如下：
[0140][0141]
s2：设定白鲸优化算法改进过程中的个体编码和解码格式，通过立方混沌映射构造具有高遍历性的映射初始订单种群。应说明的是：
[0142]
设定计量中心c(0)的车辆k承担的配送订单编号为{1，3，5，7，13}，对应订单电表种类为{a，b，a，c，d}，订单的所需电表数量为{100，160，180，150，130}。供电局v(1)的车辆j承运的订单编号为{15，18，20，21}，对应的电表种类为{c，b，a，d}，对应订单所需的电表数量为{80，50，90，75，65}，如图2所示，可根据每个订单编号确定配送电表种类及相应的收货点，也可确定其发货地点。进一步根据配送订单编号-订单种类-收货点的映射关系，将订单随机分配给不同型号的车辆上，可得到每个车辆的装载量及配送地点的路径规划方案；因此当算法进行迭代更新时，各车辆所承运的订单发生改变，进而实现车辆-订单-配送顺序的最优分配，最后得到最优的多层配送中心的车辆调度配送方案。
[0143]
在通过随机初始化的方法生成初始订单种群中，由于初始订单质量种群的好坏会很大程度上影响后续的算法的求解精度，因此在进行初始种群设计中，均匀分布的订单配送种群能使算法更好的遍历整个解空间，提高算法精度以及算法全局搜索能力。由于立方映射的效果较好，因此引入立方映射来获得多样性的订单初始种群。
[0144]
通过立方混沌映射构造具有高遍历性的映射初始订单种群包括，
[0145]
立方映射的公式如下：
[0146]
c(o+1)＝4c(o)
3-3y(o)
[0147]-1＜c(0)＜1,c(o)≠0o＝0,1,2,...
[0148]
其中，c为混沌变量，设定初始白鲸种群由nop个d维订单组成，白鲸种群数量nop映射为订单配送方案数量，白鲸种群的维度d映射为订单个数，
[0149]
首先生成之间的随机数作为每个订单配送方案中的第一维度的位置，然后根据立方映射的公式通过迭代的方法生成种群个体中每一维度的后续d-1个个体，最后将立方映射产生的变量值映射到白鲸种群个体中，具体公式如下：
[0150]
xc＝x
initial
·
(c+1)/2
[0151]
其中，xc为映射后的初始订单种群，x
initial
为初始订单种群。
[0152]
如图3所示，判断映射后的初始订单方案种群混沌解，生成初始可行订单种群解。
[0153]
若车辆所承运的订单不满足大规模电表轮换配送车辆调度模型中的约束时，则此时映射后的初始订单方案种群混沌解为不可接受解。
[0154]
若车辆所承运的订单满足大规模电表轮换配送车辆调度模型中的约束时，则此时初始混沌解为可接受解即生成初始可行订单种群解。
[0155]
s3：根据平衡因子判断白鲸优化算法是否处于探索阶段或开发阶段，建立一种基于种群分级的精英扰动机制提高白鲸优化算法后期的收敛精度和全局搜索能力。应说明的
是：
[0156]
平衡因子bf判断算法公式如下：
[0157][0158]
其中，b0为(0，1)间的随机数，t为当前迭代次数，t
max
为最大迭代次数。
[0159]
若t》t
max
，则输出最优订单方案。
[0160]
若t≤t
max
，则重新计算平衡因子和鲸落概率，进行新一轮计算。
[0161]
若平衡因子bf》0.5，则算法处于探索阶段，需通过奇偶数的选择更新订单在种群中的位置增加全局搜索能力。
[0162]
在探索阶段中，通过奇偶数的选择更新订单在种群中的位置，更新公式如下所示：
[0163][0164]
其中，为新生成的第i个订单方案中的第j个订单；pj(j＝1，2，..，d)为d维向量中随机选择的随机数，和是当前第i个订单方案和第r个订单方案的订单，r1，r2为(0，1)间的随机数，并可用于增加探索阶段的随机算子。
[0165]
若平衡因子bf≤0.5，则算法处于开发阶段，需通过引入鲸鱼优化算法的包围猎物机制增加算法的局部搜索能力。
[0166]
在开发阶段中，通过引入鲸鱼优化算法的包围猎物机制增加算法的局部搜索能力，鲸鱼优化算法的包围猎物机制可以在保证收敛性的情况下实现局部搜索的快速寻优，提高算法的寻优能力，保证算法全局搜索与局部搜索稳定进行。
[0167]
鲸鱼优化算法的包围猎物机制公式如下:
[0168][0169][0170][0171]
其中，a，c为系数向量，为t代中最优的订单配送方案，为第t代中第i个订单配送方案，为第i个t+1代得订单配送方案。
[0172]
建立一种基于种群分级的精英扰动机制提高白鲸优化算法后期的收敛精度和全局搜索能力，如图4所示，根据目标函数值将订单种群分为精英种群与劣势种群，具体公式如下：
[0173][0174]
其中，f
it
为第i个订单方案所得到的适应度函数值，为平均适应度函数值。
[0175]
若第i个订单方案所得到的适应度函数值小于平均适应度函数值，则视为精英个体。
[0176]
若第i个订单方案所得到的适应度函数值大于平均适应度函数值，则视为劣势个体。
[0177]
在精英种群中实行黄金正弦机制，提高算法的收敛速度以及最优位置的局部搜索能力，具体公式如下：
[0178][0179][0180]
其中，为第t代中第i个订单配送方案，r1为[0，2π]的随机数，决定精英个体的移动距离，r2为[0，π]的随机数，决定精英个体的移动方向，x1和x2为黄金分割系数，τ为黄金分割数。
[0181]
在劣质种群中通过白鲸种群的鲸落机制，使劣势种群跳出当前的搜索空间并找到更好的空间位置。
[0182]
在劣势种群中，若白鲸个体的勘测概率小于鲸落概率，则执行种群淘汰，若白鲸个体的勘测概率大于鲸落概率，则执行自由扰动。
[0183]
种群淘汰公式如下：
[0184][0185][0186]
wf＝0.1-0.05t/t
max
[0187]
自由扰动公式如下：
[0188][0189]
其中，为第t代中第i个订单配送方案，为第t代中第r个订单配送方案，x
step
为白鲸坠落的步长，wf为鲸鱼坠落的概率，c2为阶跃因子，ub和lb分别是订单的上限和下限，为当前种群中任意的订单配送方案。
[0190]
s4：检查迭代次数是否满足要求。应说明的是：
[0191]
设t为当前迭代次数，t
max
为最大迭代次数。
[0192]
若t》t
max
，则输出最优订单方案。
[0193]
若t≤t
max
，则重新计算平衡因子和鲸落概率，进行新一轮计算。
[0194]
本实施例还提供计及物资装载率优化的电表配送车辆路径规划系统，包括：
[0195]
模型搭建模块，用于建立大规模电表轮换配送车辆调度模型，根据每个订单编号确定配送电表种类及相应的收货点，确定每个订单发货地点。
[0196]
算法改进模块，用于改进白鲸优化算法，提高白鲸优化算法在物流调度配送中的寻优能力。
[0197]
输出模块，用于根据平衡因子判断白鲸优化算法是否处于探索阶段或开发阶段，同时检查迭代次数是否满足要求。
[0198]
本实施例还提供一种计算设备，适用于计及物资装载率优化的电表配送车辆路径规划方法的情况，包括：
[0199]
存储器和处理器；存储器用于存储计算机可执行指令，处理器用于执行计算机可执行指令，实现如上述实施例提出的计及物资装载率优化的电表配送车辆路径规划方法。
[0200]
该计算机设备可以是终端，该计算机设备包括通过系统总线连接的处理器、存储器、通信接口、显示屏和输入装置。其中，该计算机设备的处理器用于提供计算和控制能力。该计算机设备的存储器包括非易失性存储介质、内存储器。该非易失性存储介质存储有操作系统和计算机程序。该内存储器为非易失性存储介质中的操作系统和计算机程序的运行提供环境。该计算机设备的通信接口用于与外部的终端进行有线或无线方式的通信，无线方式可通过wifi、运营商网络、nfc(近场通信)或其他技术实现。该计算机设备的显示屏可以是液晶显示屏或者电子墨水显示屏，该计算机设备的输入装置可以是显示屏上覆盖的触摸层，也可以是计算机设备外壳上设置的按键、轨迹球或触控板，还可以是外接的键盘、触控板或鼠标等。
[0201]
本实施例还提供一种存储介质，其上存储有计算机程序，该程序被处理器执行时实现如上述实施例提出的实现计及物资装载率优化的电表配送车辆路径规划方法。
[0202]
本实施例提出的存储介质与上述实施例提出的数据存储方法属于同一发明构思，未在本实施例中详尽描述的技术细节可参见上述实施例，并且本实施例与上述实施例具有相同的有益效果。
[0203]
实施例2
[0204]
为本发明的另一个实施例，提供了计及物资装载率优化的电表配送车辆路径规划方法及系统的验证测试，对本方法中采用的技术效果加以验证说明。
[0205]
以仿造的云南省“计量中心-各供电局-各供电所”电表配送方案数据集为例，仿真实验过程中，使用粒子群优化算法(particleswarmoptimization，pso)，差分进化算法(differentialevolution，de)，遗传算法(geneticalgorithm，ga)，多元宇宙优化算法(multi-verseoptimizer，mvo)，传统白鲸优化算法(belugawhaleoptimization，bwo)与本发明的改进白鲸优化算法(improvedbelugawhaleoptimization，ibwo)进行对比，每个算法各进行30次仿真实验并进行对比验证，结果如下表所示：
[0206]
表1：本发明与传统方法对比。
[0207][0208]
可以看出本发明所提出的ibwo算法相较于pso算法、ga算法、de算法、mvo算法、bwo
算法在总体适应度函数值上分别降低了17.4％，11.4％，15.1％，23.9％，15.53％，优于上述算法。
[0209]
应说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本发明技术方案的精神和范围，其均应涵盖在本发明的权利要求范围当中。