一种基于PSCAD计算动车组降弓时电弧重燃模型的建模方法

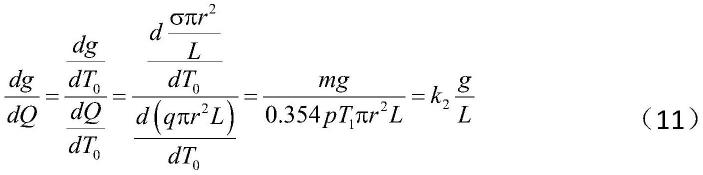
一种基于pscad计算动车组降弓时电弧重燃模型的建模方法
技术领域
1.本发明涉及高速动车组受电弓仿真领域，更具体地说，是涉及一种基于pscad计算动车组降弓时电弧重燃模型的建模方法的建立。


背景技术：

2.近年来，我国铁路事业飞速发展。然而，我国高速铁路在快速发展的过程中也会遇到各式各样的问题，其中尤以列车运行安全最为重要。为避免雪、雨、雾霾等外部自然环境的影响，目前越来越多的列车将车顶的高压设备集成在网侧柜内。网侧柜内设备众多，当出现过电压时，箱内设备可能会发生闪络。所以针对列车网侧柜内设备的电场仿真对列车安全稳定受流是至关重要的。
3.过电压的后果具体表现为：
4.由于电弧电阻呈非线性特征，一定的弓网距离对应一定的击穿电压值。在升弓过程中，随着弓网距离的减少，当实际电压小于击穿电压时，呈现大电阻特性；继续升弓一段距离，当实际电压大于击穿电压时产生电弧。该现象会导致受电弓故障等。
5.在列车降弓时会出现电弧重燃现象：当电弧电流过零前的某时刻，此时电弧电压低于起弧电压，电弧熄灭，此时在空气中留下含有正负离子的气体，记该气体间隙电压为ub。当交流电过零后，在降弓过程中，电源测电压按正弦规律变化，而受电弓车侧电压基本不变，受电弓两侧的电压差(气体间隙电压)逐渐增大。当受电弓两侧的电压差(气体间隙电压)增大到大于间隙击穿电压ub时电弧重燃；随后在交流电流过零点熄灭。如果降弓过程较慢，会重复上述过程出现多次电弧重燃与熄灭。在电弧重燃过程中会产生较高的过电压，导致绝缘设备遭到强烈冲击乃至损坏。
6.现有的关于电弧电阻仿真技术主要有，基于emtp软件的组合建模去模拟断路器跳闸前后的电弧动态特性，得出动态参数的变化波形图；基于ansoft软件对直流断路器工作过程的仿真，研究直流断路器内部器件的选取对电弧过程的影响；基于simulink工具箱的mayr 和cassie电弧仿真进行改进；基于comsol软件对交流电弧的物理场等的仿真。在参考电弧模型的建模中，发现许多学者在动车组降弓过电压建模时未考虑电弧重燃及弓网距离变化这两个问题。
7.本方案提出的仿真模型建模方法区别于现有技术，旨在提出一种仿真动车组降弓过程中电弧重燃发展变化过程和过电压演变过程的建模方法。其主要功能在于根据弓网距离变化和受电弓两侧电压差变化实时判断电弧重燃熄灭条件并实时计算电弧电阻，将计算出的电弧电阻rdf的等效数值赋予在可变rlc模块中，最终以电路中串联非线性电阻的方式来模拟受电弓下降过程中的弓网电弧发展变化过程及过电压演变过程。


技术实现要素：

8.有鉴于此，本发明提供了一种基于pscad计算动车组降弓时电弧重燃模型的建模方法，根据需要设置降弓速度及弓网间距。本发明模拟动车组降弓时电弧重燃过程引起的
过电压值的大小，通过搭建弓网模块来仿真受电弓工作时间隙击穿后的电弧电阻，进而实现给设备绝缘选型提供一项新依据的目的。
9.一种基于pscad计算动车组降弓时电弧重燃模型的建模方法，包括：
10.动车组仿真模型、弓网电弧仿真模型、间隙击穿过程仿真模型、弓网间距仿真模型、电弧可变电容仿真模型、电流过零点检测模型；
11.实现步骤如下：
12.步骤1)：根据弓网间距仿真模型输出降弓时受电弓与接触网之间的距离；
13.步骤2)：根据间隙击穿过程仿真模型输出得到降弓时弓网间击穿的时刻；
14.步骤3)：根据电流过零点检测模型输出得到电流过零点的时刻；
15.步骤4)：根据弓网电弧仿真模型输出得到受电弓下降时的弓网电弧；
16.步骤5)：根据电弧可变电容仿真模型输出得到电弧间的等效可变电容；
17.步骤6)：动车组仿真模型中输出的车侧电压波形图，通过对比前后时刻车侧电压的数值突变的情况及形状的变化可以判断电弧击穿时的过电压及电弧重燃次数。
18.优选地，所述步骤1)：弓网间距仿真模型来模拟弓网距离随着时间的变化，l为弓网距离，c1为判断弓网是否可靠接触的逻辑信号，未接触时c1为1，可靠接触时c1为0，其数学模型是：
19.l＝vt(0≤l≤0.5m)
[0020][0021]
其中v代表降弓速度。
[0022]
优选地，所述步骤2)：间隙击穿过程仿真模型中，l为步骤1) 中得到的弓网距离，输入ea受电弓与接触线之间的电压值，输出c2 为判断电弧是否击穿的信号，未击穿时c2为0，击穿时c2为1，其数学模型时：
[0023][0024][0025]
其中u代表弓网间的击穿电压，一定的弓网距离对应一定的击穿电压值。
[0026]
优选地，所述步骤3)：电流过零点检测模型中，i1为接触网与动车组间的电流，c3为i1过零点信号，其数学模型是：
[0027][0028]
其中，c3＝1代表电流过零点。
[0029]
优选地，所述步骤4)：弓网电弧仿真模型中，l为步骤1)中得到的弓网距离，rdf为电弧电阻，该电弧电阻基于步骤1)、步骤 2)、步骤3)中得到的c1、c2、c3来判断是否燃弧，即降弓时，距离l增大到一定程度时，弓网间的电压大于击穿电压，此时电弧会重燃，此时交流电流过零点时，电弧会熄灭，距离l继续增大到一定程度时，弓网间的电压又大于击穿电压，此时发生二次燃弧。其中燃弧时电弧电阻为很小的值，息弧时为无穷大，并将其最终的输出rdf的等效数值赋予在pscad中固有的可变rlc模块中，最终以电路中串联非线性电阻的方
式来模拟受电弓下降时的弓网电弧。其数学模型是：
[0030][0031]
其中g代表电弧电导；k1、k2以及β为电弧参数，其中β的取值范围为-3《β《0。
[0032]
优选地，所述步骤5)：电弧可变电容仿真模型中，l为步骤1) 中得到的弓网距离,c为可变电容的数值大小，单位为pf，并将其最终的输出c的等效数值赋予在pscad中固有的可变rlc模块中，最终以电路中与电弧电阻并联非线性电阻的方式来模拟受电弓下降时弓网间的可变电容。其数学模型是：
[0033][0034]
其中，以106代表完全断开时的电弧电容。
[0035]
优选地，所述步骤6)：动车组仿真模型中，采用27.5kv电源来代替接触网，该模型输出的车侧电压波形图中通过对比前后时刻车侧电压的幅值突变情况以及幅值突变次数来判断电弧击穿时的过电压及电弧重燃次数，其中车侧电压用e1表示。
附图说明
[0036]
图1为本技术的弓网间距仿真模型。
[0037]
图2为本技术的间隙击穿过程仿真模型。
[0038]
图3为本技术的弓网电弧仿真模型。
[0039]
图4为本技术的电弧可变电容仿真模型。
[0040]
图5为四个模型的外观设计。
[0041]
图中，l为弓网距离，c1为判断弓网是否可靠接触的逻辑信号 (未接触时c1为1，可靠接触时c1为0)，e1为受电弓与接触线之间的电压值，c2为判断弓网间是否击穿的逻辑信号(空气击穿c2输出1，未击穿输出0)，c3为判断电流是否过零点的逻辑信号(过零点时c3为1，未过零点时c3为0)，c为弓网间电弧的可变电容， k1、k2以及β为电弧参数，rdf为电弧电阻。
具体实施方式
[0042]
下面结合附图和具体实施方式对本发明进行详细说明。
[0043]
本发明提供的一种动车组升降弓过电压仿真模型，受电弓在降弓过程中随着弓头与接触线的距离不断增大会产生电弧。如图1所示为在pscad中搭建弓网间距仿真模型。升降弓时间一般在5～10s左右，工作高度为2m左右。当弓网距离小于10-6
m时，认为受电弓与接触线可靠接触，电弧也随之消失。图中输出l为弓网距离，c1为判断弓网是否可靠接触的逻辑信号，未接触时c1为1，可靠接触时c1 为0。
[0044]
随着受电弓的下降，当弓网距离增大到一定值时，空气将会击穿进而产生电弧。在标准大气压下，间隙的击穿电压与距离的经验公式如下所示：
[0045]
[0046]
式中：u为空气击穿电压，单位kv；l为弓网之间的距离，单位 cm。根据公式(1)搭建间隙击穿过程仿真模型如图2所示，e1为受电弓与接触线之间的电压值。空气击穿时c2输出1，未击穿输出0。
[0047]
在受电弓和接触网之间的空气间隙被击穿之后，会产生弓网电弧。假设此电弧半径恒定、弧柱温度沿径向均匀分布、电导率与辐射热源为温度的函数、电弧的弧柱等离子不存在空间电荷，则电弧电导g模型的推导如下所示：
[0048]
g＝f(q)＝f[∫(p-p0)dt]
ꢀꢀꢀꢀꢀꢀ
(2)
[0049][0050]
式中：p为弓网电弧的输入功率，p0为电弧输出功率，q为电弧形成中所积累的能量。p与p0均为电弧电导g的函数，具体关系如下所示：
[0051][0052]
p0＝k1g-β
l
ꢀꢀꢀꢀꢀꢀ
(5)
[0053]
式中：i为电弧电流，l为电弧弧长，k1、β为常数。
[0054]
将以上关系式整理得：
[0055][0056]
电弧总能量q及电弧电导g为：
[0057]
q＝qπr2l
ꢀꢀꢀꢀꢀꢀꢀ
(7)
[0058][0059]
根据气体分子运动理论，推导单位体积电弧积累的能量q为：
[0060][0061]
式中：p为大气压强，t1为外界环境温度，t0为所产生电弧的温度。假定大气压强p以及压定比热容都是常数，由电弧理论的萨哈公式推导出电弧电导率σ为：
[0062][0063]
式中：σ0为电弧单位长度电导，m为系数。
[0064]
可以看出电弧总能量q及电弧电导g均为电弧温度t0的函数，由以上一系列公式可推得：
[0065]
[0066]
将公式(11)代入公式(6)得：
[0067][0068]
公式(12)就是最终的电弧模型，k1、k2以及β为电弧参数，根据文献描述及对电弧机理分析。β的取值范围为-3《β《0。根据公式(12) 在pscad中搭建弓网电弧仿真模型如图3所示，rdf为电弧电阻。
[0069]
随着弓网间距的增大，受电弓与接触网之间会存在一个与弓网间距有关的可变电容，在pscad中搭建电弧可变电容仿真模型如图4所示，该模型的公式为：
[0070][0071]
在受电弓完全降下来时，弓网间的电容近似为0.5pf，在受电弓与接触网完全分离之前(弓网间距l《0.1mm)时的可变电容取1
×
10
6 pf。
[0072]
根据以上所介绍的弓网距离、间隙击穿过程、弓网电弧以及可变电容四个模型，将其在pscad软件中共同创建。其中弓网电弧仿真模型并将其最终的输出电弧电阻rdf的等效数值赋予在pscad中固有的可变rlc模块中，以电路中串联非线性电阻的方式来模拟受电弓上升和下降时的弓网电弧，最终在模型输出的车侧电压波形图中通过对比前后时刻车侧电压的幅值突变情况以及幅值突变次数可以判断电弧击穿时的过电压及电弧重燃次数。
[0073]
以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，凡依本发明申请专利范围所作的均等变化或修饰，都属本发明涵盖范围之内。