一种实现线激光3D相机高精度测量外圆柱面的校准方法

一种实现线激光3d相机高精度测量外圆柱面的校准方法
技术领域
1.本发明是涉及一种实现线激光3d相机高精度测量外圆柱面的校准方法，属于图像测量 技术领域。


背景技术：

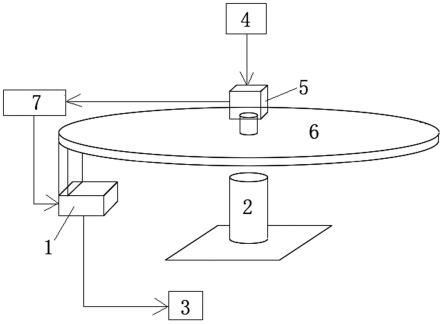
2.线激光3d相机在工业中可用于圆柱工件3维重建，利用该相机激光扫描圆柱工件外表 面，并通过捕获激光线，可利用三角法来计算圆柱工件外表面的深度信息和保存该位置的 灰度值和深度值。具体如附图1所示，3d相机被固定在由回转电机控制驱动的回转平台上， 回转电机由plc控制器驱动并自带编码器，相机工作模式为编码器触发的线扫描方式，通 过编码器的触发信号来保证相机和回转的同步执行，工作的时候，plc控制器驱动回转电 机转动，回转电机驱动回转平台转动进而带动3d相机转动，与此同时，回转电机上的编码 器向3d相机发送触发信号，3d相机接收到编码器的触发信号后对圆柱工件进行扫描，这 样即可通过编码器的触发信号来保证相机和回转的同步执行，相机每次采样均可获得该位 置的一条轮廓信息，逐条扫描形成圆柱工件外表面的深度图像，形成的深度图像最后发送 至计算机进行处理。
3.但是在实际工程应用中，由于3d相机和圆柱工件的安装误差会导致数据无法直接被使 用，主要表现在：1)圆柱工件安装时会存在一定偏心，导致数据在深度方向上会存在一定 偏移量；2)3d相机在安装时无法保证相机的激光线方向与回转轴线在同一平面，存在一定 切向偏差，这会导致扫描出来的深度信息会有径向扭曲现象；当圆柱工件安装偏心量较大 时，由切向偏差引起的扭曲现象会加剧。
4.为了能够实现高精度测量外圆柱面，需要对扫描出来的深度信息进行校准，以消除安 装误差带来的影响，但现有线扫描校正方法均无法对外圆柱面进行校准，从而影响了3d相 机对圆柱工件外表面的高精度测量。


技术实现要素：

5.针对现有技术存在的上述问题，本发明的目的是提供一种实现线激光3d相机高精度测 量外圆柱面的校准方法。
6.为实现上述目的，本发明采用如下技术方案：
7.一种实现线激光3d相机高精度测量外圆柱面的校准方法，包括如下步骤：
8.s1、通过线激光3d相机获取圆柱工件外表面的深度图像，并将深度图像传递给计算机， 计算机记录深度图像的每一行数据的深度信息和坐标信息，并对每行深度信息利用 ransac方法去除数据中存在的异常点，再对剩余点进行最小二乘法，然后计算每行的平 均深度并记录；
9.s2、遍历深度图像的每一行数据，并将每行数据记录的平均深度根据其所对应的角度 生成圆柱工件的深度变化集合；
10.s3、建立圆柱工件的偏心深度变化函数关系式并对深度变化集合进行拟合，通过
变化 曲线计算圆柱工件的偏心量及偏心方向角，并记录各点的拟合偏差；
11.s4、建立相机偏移深度变化函数关系式并对拟合偏差进行拟合，通过变化曲线计算相 机的偏移量，并记录各点的拟合偏差；
12.s5、重复步骤s3、s4操作，直至圆柱工件的偏心量、偏心方向角和相机偏移量与上一 轮数据之差均小于预设值，结束迭代。
13.一种实施方案，步骤s1的具体操作如下：
14.a)通过plc控制器驱动回转电机，回转电机驱动回转平台回转进而带动回转平台上的 线激光3d相机回转，同时回转电机上的编码器向线激光3d相机发送触发信号，线激光3d 相机接收到编码器的触发信号后对圆柱工件进行激光扫描，以获取圆柱工件外表面的深度 图像并将深度图像传递给计算机；
15.b)计算机记录深度图像的每一行数据的深度信息和坐标信息：
16.设定第i行第j列数据的深度信息为坐标信息为则第i行 的数据集合
17.c)计算机对深度信息利用ransac方法去除数据中存在的异常点，然后对剩余点进行 最小二乘法，再计算每行的平均深度并记录：
18.设定原始深度图像尺寸为h
×
w，横向单位像素对应实际间距xr为(360/h)
°
/piexl，纵向 单位像素对应实际间距yr为相机预设参数；从集合hi中随机抽取n个点作为初始样本 拟合直线li，设定直线li方程为h＝a0y+b0；
19.将初始样本中所有的点代入直线方程li并计算平均损失函数loss0：
20.式中为初始样本中第j个点对 应的深度信息，a0和b0分别为直线方程li中的初始拟合参数，是的理论值； 为第i行第j列数据的纵坐标；
21.为求平均损失函数loss0的极小值，分别令loss0对a0和b0的导数取0：
[0022][0023]
对上式化简得：
[0024][0025]
计算出参数a0和b0后，则直线li方程为h＝a0y+b0；
[0026]
将直线li方程化作一般直线方程ax+by+c＝0的形式，遍历点集hi中剩余的点 (y
p
,h
p
)，并计算该点到拟合直线的距离d
p
：
[0027][0028]
设定距离阈值thresh，通过下式判断该点是否为内点，若为内点则加入样本集中：
[0029]
若d
p
＜thresh，则为内点；若d
p
≥thresh，则为外点；
[0030]
待一轮遍历完成后，用样本集重新拟合新的直线方程并进行新一轮迭代；经10～30次 的迭代后，将内点数最多的样本集作为最佳样本集，并将其对应的直线方程作为最佳直线 方程；最后根据最佳直线方程结合该样本集中y坐标的范围，得到该扫描轮廓的平均深度 [0031]
一种实施方案，步骤s2的具体操作如下：
[0032]
记录深度图像的每一行数据的深度信息和坐标信息的同时，还记录编码器向线激光3d 相机发送触发信号时所对应的回转平台的转角θ；
[0033]
计算机遍历深度图像的每一行数据，并将每行数据记录的平均深度根据其所对应的回 转平台的转角生成圆柱工件的深度变化集合y：
[0034]
式中，分别是回 转平台的转角为θ0、θ1、θ
w-1
时所对应的平均深度，其中，θ满足 w为深度图像的宽度。
[0035]
一种实施方案，步骤s3的具体操作如下：
[0036]
以回转平台的中心o1为原点建立x-y坐标系，设定圆柱工件的半径为r1，圆心坐标
为 (δx,δy)，偏心量为则偏心方向角α满足：
[0037]
在δo1o2b
θ
中，利用余弦定理可得：o2b
θ2
＝o1o
22
+o1b
θ2-2
·
o1o2·
cos∠b
θ
o1o2，式 中，o2为圆柱工件实际中心，b
θ
为回转平台的转角为θ时3d相机激光线与圆柱工件轮廓 的交汇点，o1o2为回转平台中心到圆柱工件实际中心的距离，即偏心量δr，o2b
θ
为圆柱工 件实际中心到3d相机激光线与圆柱工件轮廓的交汇点的距离，即圆柱工件的半径r1；o1b
θ 为回转平台的中心到3d相机激光线与圆柱工件轮廓的交汇点的距离；
[0038]
化简可得：
[0039]
o1b
θ2-2
·
δr
·
cos(α-θ)
·
o1b
θ
+δr
2-r
12
＝0；
[0040]
利用求根公式可得：
[0041][0042]
由于r1＞＞δr，所以可近似认为：
[0043][0044]
结合o1b
θ
＞0，可得：
[0045]
o1b
θ
＝δr
·
cos(α-θ)+r1；
[0046]
则圆柱工件的偏心深度变化函数关系式为：
[0047]hθ
＝a
θbθ
＝a
θo1-b
θ
o1＝r-r
1-δr
·
cos(α-θ)，式中：h
θ
为回转平台的转角 为θ时所对应的圆柱工件的偏心深度，a
θ
为回转平台的转角为θ时3d相机的位置，r为 3d相机的回转半径；
[0048]
令a1＝-δr，b1＝r-r1，则h
θ
＝a1·
cos(α-θ)+b1；
[0049]
将深度变化集合y中所有点代入上式并计算平均损失函数loss1：
[0050]
式中，h
θ
为深度变化集合 y中对应回转角为θ时的平均深度，为h
θ
的理论值；
[0051]
由于loss1表达式为非线性且含多个变量即a1、b1和α，为求平均损失函数loss1的极小 值，建立对应hession矩阵如下：
[0052]
其中，x为输入参数，满足 x＝(a1b1α)
t
；
[0053]
平均损失函数loss1的梯度定义为：
[0054][0055]
其中：
[0056][0057]
则最终的迭代公式为：
[0058]
其中x0为参数初始值，这里取(1 1 0)，为的逆矩阵。
[0059]
一种实施方案，步骤s4的具体操作如下：
[0060]
以回转平台的中心o1为原点建立x-y坐标系，线激光3d相机的理想位置为点a，线 激光3d相机的实际位置为点c，偏移量为δc，由于偏移量的存在会使线激光3d相机的 激光线与圆柱工件的交汇点发生偏移，即从原来的b点偏移至d点，导致最后3d相机测 量出来的距离由原先的ab变成了cd，故需建立δc与ab和cd之差即eb之间的关系式；
[0061]
根据相对运动关系，固定线激光3d相机的坐标，得出圆柱工件的圆心相对坐标为： (r2·
cosθ,r2·
sinθ)，r2为圆柱工件的运动半径，则点b、点d将满足下式：
[0062][0063]
式中：(xb,yb)、(xd,yd)分别为点b和点d的坐标，r1为圆柱工件的半径；
[0064]
将上式化简得：
[0065][0066]
故
[0067]
令步骤s3中的将深度变化集合y中所有点代入eb表达式并计 算对应的平均损失函数loss2：
[0068][0069]
式中，为δh
θ
的理论值；
[0070]
对应牛顿迭代公式为：
[0071]
式中，δc0为偏差初始值，这里设为0，δcn为δc0经 n次迭代后的结果，loss2'(δc)为loss2(δc)的导数。
[0072]
相较于现有技术，本发明的有益技术效果在于：
[0073]
本发明基于基本数学模型，通过充分考虑线激光3d相机扫描圆柱工件所存在的硬件误 差，实现了自适应误差消除，从而保证了对圆柱工件的外圆柱面的高精度测量，相对于现 有技术，具有显著进步性和应用价值。
附图说明
[0074]
图1是本发明中所述的线激光3d相机测量圆柱工件外圆柱面的工作流程示意图；
[0075]
图2是本发明实施例提供的对圆柱工件偏心的测量原理示意图；
[0076]
图3是本发明实施例提供的对线激光3d相机偏移的测量原理示意图；
[0077]
图中标号示意如下：1、线激光3d相机；2、圆柱工件；3、计算机；4、plc控制器； 5、回转电机；6、回转平台；7、编码器。
具体实施方式
[0078]
以下将结合附图和实施例对本发明的技术方案做进一步清楚、完整地描述。
[0079]
实施例
[0080]
请结合图1至图3所示：本发明提供的一种实现线激光3d相机高精度测量外圆柱面的 校准方法，包括如下步骤：
[0081]
s1、通过线激光3d相机1获取圆柱工件2外表面的深度图像，并将深度图像传递给
计 算机3，计算机3记录深度图像的每一行数据的深度信息和坐标信息，并对深度信息利用 ransac方法去除数据中存在的异常点，再对剩余点进行最小二乘法，然后计算每行的平 均深度并记录，具体如下：
[0082]
a)如图1所示，通过plc控制器4驱动回转电机5，回转电机5驱动回转平台6回转进 而带动回转平台6上的线激光3d相机1回转，同时回转电机5上的编码器7向线激光3d 相机1发送触发信号，线激光3d相机1接收到编码器7的触发信号后对圆柱工件2进行扫 描，以获取圆柱工件2外表面的深度图像并将深度图像传递给计算机3；
[0083]
b)计算机3记录深度图像的每一行数据的深度信息和坐标信息：
[0084]
设定第i行第j列数据的深度信息为坐标信息为则第i行 的数据集合
[0085]
c)计算机对深度信息利用ransac方法去除数据中存在的异常点，再对剩余点进行最 小二乘法，然后计算每行的平均深度并记录：
[0086]
设定原始深度图像尺寸为h
×
w，横向单位像素对应实际间距xr为(360/h)
°
/piexl，纵向 单位像素对应实际间距yr为相机预设参数，本实施例中，yr设为0.1mm，xr设为0.1
°
； 从集合hi中随机抽取n个点作为初始样本拟合直线li， 设定直线li方程为h＝a0y+b0；
[0087]
将初始样本中所有的点代入直线方程li并计算平均损失函数loss0：
[0088]
式中为初始样本中第j个点对应的 深度信息，a0和b0分别为直线方程li中的初始拟合参数，是的理论值；
[0089]
为求平均损失函数loss0的极小值，分别令loss0对a0和b0的导数取0：
[0090][0091]
对上式化简得：
[0092][0093]
计算出参数a0和b0后，则直线li方程为h＝a0y+b0；
[0094]
将直线li方程化作一般直线方程ax+by+c＝0的形式，遍历点集hi中剩余的点 (y
p
,h
p
)，并计算该点到拟合直线的距离d
p
：
[0095][0096]
设定距离阈值thresh，通过下式判断该点是否为内点，若为内点则加入样本集中：
[0097][0098]
待一轮遍历完成后，用样本集重新拟合新的直线方程并进行新一轮迭代，经10～30次 迭代后(本实施例中迭代次数取20)，将内点数最多的样本集作为最佳样本集并将对应直线 方程作为最佳直线方程；最后根据最佳的直线方程结合该样本集中y坐标的范围，得到该扫 描轮廓的平均深度
[0099]
s2、遍历深度图像的每一行数据，并将每行数据记录的平均深度根据其所对应的角度 生成圆柱工件的深度变化集合，具体为：
[0100]
记录深度图像的每一行数据的深度信息和坐标信息的同时还记录编码器向线激光3d相 机发送触发信号时所对应的回转平台的转角θ；
[0101]
计算机遍历深度图像的每一行数据，并将每行数据记录的平均深度根据其所对应的回 转平台的转角生成圆柱工件的深度变化集合y：
[0102]
式中，分别是回 转平台的转角为θ0、θ1、θ
w-1
时所对应的平均深度，其中，θ满足
[0103]
s3、建立圆柱工件的偏心深度变化函数关系式并对深度变化集合进行拟合，通过
变化 曲线计算圆柱工件的偏心量及偏心方向角，并记录各点的拟合偏差，具体为：
[0104]
参见图2所示，以回转平台的中心o1为原点建立x-y坐标系，并设定圆柱工件的半径 为r1，圆心坐标为(δx,δy)，偏心量为则偏心方向角α满足：此外，本实施例图2中，o2为圆柱工件实际中心，r为3d相机的回转轨迹 半径，a0、a
θ
和a
90
分别为回转平台的转角为0
°
、θ
°
和90
°
时所对应的3d相机的位置，b0、b
θ
和b
90
分别为回转平台的转角为0
°
、θ
°
和90
°
时，3d相机激光线与圆柱工件的轮廓的交 汇点；
[0105]
在δo1o2b
θ
中，利用余弦定理可得：o2b
θ2
＝o1o
22
+o1b
θ2-2
·
o1o2·
cos∠b
θ
o1o2[0106]
式中：o1o2为回转平台中心到圆柱工件实际中心的距离，即偏心量δr，o2b
θ
为圆柱工 件实际中心到3d相机激光线与圆柱工件轮廓的交汇点的距离，即圆柱工件的半径r1；o1b
θ 为回转平台的中心到3d相机激光线与圆柱工件轮廓的交汇点的距离；
[0107]
化简可得：
[0108]
o1b
θ2-2
·
δr
·
cos(α-θ)
·
o1b
θ
+δr
2-r
12
＝0；
[0109]
利用求根公式可得：
[0110][0111]
由于r1＞＞δr，所以可近似认为：
[0112][0113]
结合o1b
θ
＞0，可得：
[0114]
o1b
θ
＝δr
·
cos(α-θ)+r1；
[0115]
则圆柱工件的偏心深度变化函数关系式为：
[0116]hθ
＝a
θbθ
＝a
θo1-b
θ
o1＝r-r
1-δr
·
cos(α-θ)，式中：h
θ
为回转平台的转角为θ时 所对应的圆柱工件的偏心深度，a
θ
为回转平台的转角为θ时所对应的3d相机的位置，r为 3d相机的回转半径。
[0117]
令a1＝-δr，b1＝r-r1，则h
θ
＝a1·
cos(α-θ)+b1；
[0118]
将深度变化集合y中所有点代入上式并计算平均损失函数loss1：
[0119][0120]
式中h
θ
为深度变化集合y中对应回转角为θ的平均深度，为h
θ
的理论值；
[0121]
由于loss1表达式为非线性且含多个变量即a1、b1和α，为求平均损失函数loss1的极小 值，建立对应hession矩阵如下：
[0122]
其中，x为输入参数，满足 x＝(a1b1α)
t
；
[0123]
平均损失函数loss1的梯度定义为：
[0124][0125]
其中：
[0126][0127]
则最终的迭代公式为：
[0128]
其中x0为参数初始值，这里取(1 1 0)，为h
loss
(x)的逆矩阵；
[0129]
s4、建立相机偏移深度变化函数关系式并对拟合偏差进行拟合，通过变化曲线计算相 机的偏移量，并记录各点的拟合偏差，具体为：
[0130]
参见图3所示，以回转平台的中心o1为原点建立x-y坐标系，线激光3d相机理想位 置为点a，实际位置为点c，偏移量为δc，由于偏移量的存在会使线激光3d相机的激光 线与圆柱工件的交汇点发生偏移即从原来的b点偏移至d点，导致3d相机测量出来的深 度由原先的ab变成了cd，故需建立δc与ab和cd之差即eb之间的关系式；图3中， ab为理想的测量深度，cd为实际的测量深度，eb为理想与实际测量深度的偏差，o2为 圆柱工件实际中心，e为点d在ae上的投影，圆柱工件的中心由o2运动至o2'，此时 b、d、e点运动至b'、d'、e'；
[0131]
根据相对运动关系，固定线激光3d相机的坐标，得出圆柱工件的圆心相对坐标为： (r2·
cosθ,r2·
sinθ)，r2为圆柱工件的运动半径，则点b、点d将满足下式：
[0132][0133]
式中：(xb,yb)、(xd,yd)分别为点b和点d的坐标，r1为圆柱工件的半径；
[0134]
将上式化简得：
[0135][0136]
故
[0137]
令步骤s3中的将深度变化集合y中所有点代入eb表达式并计 算对应的平均损失函数loss2：
[0138][0139]
式中，为δh
θ
的理论值；
[0140]
对应牛顿迭代公式为：
[0141]
式中，δc0为偏差初始值，这里设为0，δcn为δc0经 n次迭代后的结果，loss2'(δc)为loss2(δc)的导数。
[0142]
s5、重复步骤s3、s4操作，直至圆柱工件的偏心量、偏心方向角和相机偏移量与上一 轮数据之差均小于预设值，结束迭代。
[0143]
最后有必要在此指出的是：以上所述仅为本发明较佳的具体实施方式，但本发明的保 护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻 易想到的变化或替换，都应涵盖在本发明的保护范围之内。