一种采用粒子群优化的三维模型最优视角选择方法与流程

recognition, vol. 2, pp. 273
–
276 (2004)”将选择在视角相似性上最具代表性的视角作为目标，相似的视角聚类在一起，不同的类中心形成了具有代表性的视角子集，但这些方法是基于k-均值聚类的，需要用户指定聚类个数；文献“ansary tf, daoudi m, vandeborre j.-p.: a bayesian 3-d search engine using adaptive views clustering. ieee trans. multimed.9(1), 78
–
88 (2007)”针对这一问题提出了一种改进的x-均值算法，聚类的数量可自适应于模型的复杂性；文献“podolak j, shilane p, golovinskiy a, rusinkiewicz s, funkhouser t.: a planar-reflective symmetry transform for 3dshapes. acm trans. graph, pp. 549
–
559 (2006)”以减少视角对称性为目标，选择对称性最小的视角作为最优视角；公开号cn103295025b、发明名称为《一种三维模型最优视图的自动选择方法》中，将最优视角选择问题归结为特征选取以及分类问题，考察视角对不同类模型的区分性能，某一类模型各个视角中区分能力最好的视角即为最优视角，但是该方法需要大量的样本数据来训练分类器，对于小样本数据则难以获得理想的选择结果。这类方法将模型最优视角选择问题归结为各自所定义目标的最优问题，然而使得目标最优的视角并不一定拥有较大的信息量和符合人们的主观倾向。
5.第二类方法的目的是最大化视角可见特征。在这类方法中，首先通过在模型的包围球面上采样获得候选视角集合，有助于减少最优视角的搜索空间；然后选择视角可见模型特征，部分方法还会为这些特征赋予权重以衡量其重要性；最后通过函数为各视角打分选择得分最高视角作为最优视角。这类方法的关键在于特征的选取以及权重的设定。文献“v
á
zquez p-p, feixas m, sbert m, heidrich w.: viewpoint selection using viewpoint entropy. in: proceedings of the vision modeling and visualization conference vmv, (2001).
ꢀ’
01, pp. 273
–
280. aka gmbh (2001)”提出利用曲面面积熵来衡量模型的几何复杂性，将模型每一面片可见部分投影面积相对于整个模型可见部分投影面积之比作为面片概率，并选取面积熵最大的视点作为最优观察视点；文献：曹伟国，胡平，李华，林宗楷。基于距离直方图的最优视点选择。计算机辅助设计与图形学学报，2010，22(9)：1515-1521).在三维物体表面均匀采样获取采样点并计算物体形心，利用采样点到物体形心的距离来构造距离直方图，计算距离直方图的shannon熵作为衡量视角优劣的标准；文献“杨利明，王文成，吴恩华。基于视平面上特征计算的视点选择。计算机辅助设计与图形学学报，2008，20(9)，1097-1103”定义了基于视平面的一种曲率特征，并由此计算与视角相关的一种熵值，将熵值最大的视角作为最优视角。上述方法选择最优视角主要只是考虑模型的几何特征，所选取的视角在可见信息量上相对第一类方法有较好的表现，但在视角的亲和舒适性上的考虑还不足。文献“michela m, michela s. semantics-driven best view of 3d shapes. computers & graphics 33 (2009) 280
–
290”认为最优视角应当和模型的语义组成部分密切相关，利用面向语义的分割方法来分割模型来获取有意义的部分，不同分割方法的分割片段具有不同的特征权重，作者设计了一种权重函数对候选视角集合进行打分以获得最优视角。该方法除了把握视角的几何特征，还考虑到了模型的语义含义。但是由于特征的选取对于视角亲和舒适性的把握仍显不足；并且特征权重是对应于分割方法，并通过大量实验统计分析后得到各种分割方法最终的权重值，难以保证适用于所有使用该分割方法的模型类。所以所选择的部分视角并不是很理想，视角常常还是以最大化模型可见部分或信息量为标准，并且在视角亲和舒适度上依然有所欠缺。


技术实现要素：

6.发明目的：本发明所要解决的技术问题是针对现有技术的不足，提供一种采用粒子群优化的三维模型最优视角选择方法，包括以下步骤：步骤1，对已分类的三维模型集进行预处理，所述三维模型集中包含有三维数字几何模型数据；步骤2，基于预处理后的三维模型集，学习最优权重配置；步骤3，对三维模型选择最优视角。
7.步骤1包括：步骤1-1，对三维模型数据进行姿态校正；步骤1-2，对三维模型数据进行标准化分割。
8.步骤1-1包括以下步骤：步骤1-1-1，计算三维模型的中心，将三维模型平移至以三维模型的中心为原点的坐标系上；步骤1-1-2，通过pca(principal component analysis，主成成分分析)方法计算三维模型的主轴方向（一般是通过文献“pearson k. on lines and planes of closest fit to systems of points in space[j]. philosophical magazine, 1901, 2(6): 559-572”提出的pca方法计算模型的主轴方向）；步骤1-1-3，将各个三维模型通过pca方法得到的主轴正方向调整至与坐标系的z轴正方向一致。
[0009]
步骤1-2包括：将同类三维模型按统一的标准分割为两个以上语义部件（以人体模型为例，可统一分割为头部、双手、双脚、躯干四个部件，其他类别模型保持标准统一的分割方式即可），同类三维模型拥有相同的语义部件个数以及相同的语义标签。
[0010]
步骤2包括：步骤2-1，获取三维模型的视角标定序列；步骤2-2，学习三维模型的最优视角角度；步骤2-3，设计三维模型视角的权重函数；步骤2-4，学习三维模型视角的最优权重配置。
[0011]
步骤2-1包括：步骤2-1-1，对于任一类的三维模型，选出其中n个三维模型作为训练模型集合m={m1,m2,
…
,mn}，其中mn表示第n个三维模型；计算各训练模型顶点两两之间的距离，选择最长的顶点之间的距离记为r
max
，生成包围模型的正20面体，正20面体中心与坐标原点重合，正20面体中心到顶点的距离为r
max
；步骤2-1-2，计算各三角面重心所在半径与正20面体各顶点所在球面的交点，所求交点与正20面体各顶点形成候选视角所在位置的集合，共32个，记为；步骤2-1-3，对每个训练模型生成各视角所见的模型视图；步骤2-1-4，对各训练模型的模型视图集合进行排序，计算各视角与模型主轴方向
的夹角θ作为排序依据，θ越接近45
°
则排序越靠前，所得n个排序序列即为训练模型候选视角的标定排序序列。
[0012]
步骤2-2包括以下步骤：步骤2-2-1，n个训练模型的标定排序序列中，排在首位的视角即为模型的最优视角，排在首位的视角形成训练模型的最优视角集合v_best={v
best1
, v
best1
,
…
,v
bestn
}，其中v
bestn
表示第n个训练模型的最优视角；各最优视角一一对应着从坐标原点到视点所在位置的向量，计算集合v_best中第i个最优视角对应向量v
besti
与模型竖直方向向量n的夹角di，形成最优视角角度集合degree={ d1, d2,
…
, dn}，其中i取值为1~n；步骤2-2-2，使用k-means方法对集合degree进行聚类，将各最优视角角度根据角度之间的距离|d
besti ‑ꢀdbestj
|进行聚类，计算各聚类中心，将类中心之间距离小于所设定阈值的类再次进行聚类，重复这一操作直到不能再进行进一步聚类，并计算最终所得各聚类中心的最优视角角度作为模型的最优视角角度集合，记为degree_best={d
best1
,d
best2
,
…
,d
bestm
}，m为最终的聚类个数，d
besti
表示第i个聚类中心的最优视角角度。
[0013]
步骤2-3包括以下步骤：步骤2-3-1，计算三维模型分段可见性：其中为从视角v可见的分段s的顶点数，为分段s的总顶点数；计算分段相关性：其中 为分段s的表面积，为模型的m的总表面积；步骤2-3-2，计算三维模型分段数目可见性：其中为从视角v可见的分段数目，n为模型分段总数目；步骤2-3-3，对于模型的候选视角v，计算视角对应的向量与模型竖直方向的夹角dv；选择模型对应的degree_best集合中与dv最接近的角度d
besti
，候选视角v的亲和度定义为：；步骤2-3-4，将模型分段si的可见性与相关性的乘积作为特征赋予权重，分段数目可见性赋予权重视角亲和性赋予权重，设计权重函数形式如下：
。
[0014]
步骤2-4包括以下步骤：步骤2-4-1，在权重空间随机选择k种（一般可取值10）权重配置，权重空间由各权重的不同组合构成；步骤2-4-2，对每一个训练模型和每一种权重配置，使用权重函数计算各候选视角得分；步骤2-4-3，根据得分，将候选视角进行从高到低排序，获得排序序列；步骤2-4-4，将每一个训练模型的候选视角的排序序列与对应的标定序列计算距离，对于第i个视角，，设定在标定序列中所处的位置为，再计算得分所得的排序序列所处的位置为，两个位置之间的距离用下式表示：对每个视角都计算出对应的距离并相加，将和值作为标定序列和得分所得的排序序列之间的距离，如下式所示：；步骤2-4-5，将每一种权重配置下，各训练模型的视角排序距离求和，选出距离之和最小的权重配置；步骤2-4-6，在距离之和最小的权重配置临近的权重空间内继续随机选取k种权重配置，迭代上述过程，直到达到迭代终止条件，迭代终止条件为以下三种的任一种：序列距离已达到所设定的阈值；一轮迭代下已经无法再获得更优的解，即更小的序列距离之和；迭代次数达到设定的上限；步骤2-4-7，迭代过程结束后，得到三维模型最优的权重配置。
[0015]
步骤3包括：对于其他已经过预处理的非训练三维模型，对各候选视角提取特征，通过权重函数对候选视角打分，选择得分最高的视角作为最优视角。
[0016]
本发明设计了一种对候选最优视角打分的权重函数，该函数中的特征选取不仅考虑了视角能够看到三维模型尽可能多的几何特征，即信息量较大，同时也考虑了所选视角的亲和舒适性，尽量接近人们观察物体常用的视角；另外本发明采用粒子群优化方法对模型进行分类别学习，获取最适合于该类模型的权重值，从而获取权重函数中各个特征的权重配置。利用权重函数对模型各个候选视角进行打分，得分最高的视角即为最优视角。
[0017]
有益效果：本发明是一种通用的最优视角选择方法，可以适用于多种类别的三维模型；其次，本发明对三维模型库的大小没有严格的要求，不同大小的模型库均可获得较理
想的视角选择结果；最后，本发明得到的最优视角很符合多数人倾向的观察视角。
附图说明
[0018]
下面结合附图和具体实施方式对本发明做更进一步的具体说明，本发明的上述和/或其他方面的优点将会变得更加清楚。
[0019]
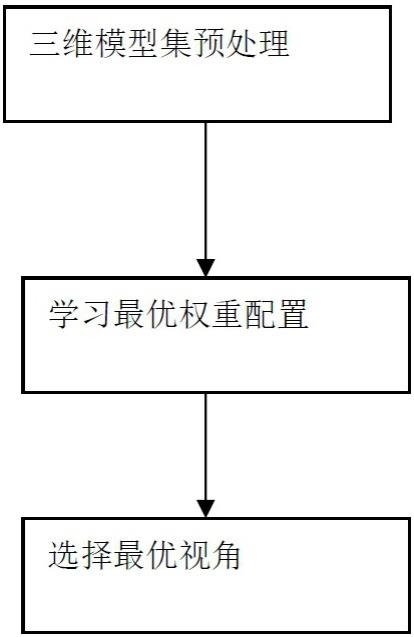
图1是本发明的处理流程示意图。
[0020]
图2是本发明模型标准化分割示意图。
[0021]
图3是三维模型候选视角示意图。
[0022]
图4a是实施例的输入模型集示例示意图。
[0023]
图4b是实施例的输入模型集示例示意图。
[0024]
图4c是实施例的输入模型集示例示意图。
[0025]
图5a是对三维模型提取得到的最优视角的示意图。
[0026]
图5b是对三维模型提取得到的最优视角的示意图。
[0027]
图5c是对三维模型提取得到的最优视角的示意图。
具体实施方式
[0028]
如图1所示，本发明公开的一种采用粒子群优化的三维模型最优视角选择方法，具体包括以下步骤：步骤1，三维模型集预处理：对已分类的三维模型集进行预处理以减少三维模型不同姿态和同类模型非标准化分割的影响，包括姿态校正和标准化分割两个步骤。
[0029]
步骤2，学习最优权重配置：对每一类模型取出部分模型作为训练数据，提取特征，并通过学习方法获得每一类模型最优的权重配置，包括获取视角标定序列，学习最优视角角度，设计权重函数和学习最优权重配置四个步骤。
[0030]
步骤3，选择最优视角：对于其他已经过预处理非训练模型，通过权重函数对候选视角打分，选择得分最高的视角作为最优视角。
[0031]
本发明的输入三维模型集为已分好类的三维模型集合。
[0032]
下面具体介绍各个步骤的主要流程：（1）三维模型集预处理三维模型集预处理：对已分类的三维模型集进行预处理以减少三维模型不同姿态和同类模型非标准化分割的影响，包括姿态校正和标准化分割两个步骤。
[0033]
1.1姿态校正姿态校正过程调整三维模型的坐标系，将三维模型的姿态校正为直立状态，减少三维模型不同姿态的影响。过程如下：步骤1-1-1，计算三维模型的中心，将三维模型平移至以该模型的中心为原点的坐标系上；步骤1-1-2，通过pca方法计算模型的主轴方向；步骤1-1-3，将各个模型通过pca方法得到的主轴正方向调整至与坐标系的z轴正方向一致。
[0034]
1.2标准化分割
of 3d shapes. computers & graphics 33 (2009) 280
–
290”中提出的分段可见性（feature visibility），分段相关性（feature relevance）作为视角特征。分段可见性为模型在某一视角下各分段可见顶点数目与该分段所有顶点数之比：各分段可见顶点数目与该分段所有顶点数之比：为从视角v可见的分段s的顶点数，为分段s的总顶点数；分段相关性为模型各分段表面积与模型总表面积之比：性为模型各分段表面积与模型总表面积之比： 为分段s的表面积，为模型的m的总表面积。
[0043]
步骤2-3-2，采用分段数目可见性作为视角特征。分段数目可见性为模型在某视角下可见的分段数目与总分段数目之比：可见的分段数目与总分段数目之比：为从视角v可见的分段数目，n为模型分段总数目。
[0044]
步骤2-3-3，采用视角亲和度作为视角特征。对于某个模型的某候选视角v，计算该视角对应的向量与模型竖直方向的夹角dv；选择该类模型对应的degree_best集合中与dv最接近的角度d
besti
，候选视角v的亲和度定义为：步骤2-3-4，步骤2-3-4，将模型分段si的可见性与相关性的乘积作为特征赋予权重，分段数目可见性赋予权重视角亲和性赋予权重，设计权重函数形式如下：。
[0045]
2.4学习最优权重配置学习最优权重配置通过粒子群优化算法来获得权重函数中各类模型各特征的最优权重配置。过程如下：步骤2-4-1，在权重空间随机选择k种权重配置。
[0046]
步骤2-4-2，对每一个训练模型和每一种权重配置，使用权重函数计算各候选视角得分。
[0047]
步骤2-4-3，根据得分，将候选视角进行从高到低排序，获得排序序列。
[0048]
步骤2-4-4，将每一个训练模型的候选视角的排序序列与对应的标定序列计算距离，对于第i个视角，，设定在标定序列中所处的位置为，再计算得分
所得的排序序列所处的位置为，两个位置之间的距离用下式表示：对每个视角都计算出对应的距离并相加，将和值作为两个序列之间的距离，如下式所示：；步骤2-4-5，将每一种权重配置下，各训练模型的视角排序距离求和，选出距离之和最小的权重配置；步骤2-4-6，在距离之和最小的权重配置临近的权重空间内继续随机选取k种权重配置，迭代上述过程，直到达到迭代终止条件，迭代终止条件为：（1）序列距离已达到所设定的阈值，该阈值可根据具体情况设定；（2）某一轮迭代下已经无法再获得更优的解，即更小的序列距离之和；（3）迭代次数达到设定的上限。
[0049]
步骤2-4-7，迭代过程结束后，可得到该类模型最优的权重配置。
[0050]
（3）选择最优视角最优视角选择：对于其他已经过预处理非训练模型，对各候选视角提取特征，通过权重函数对候选视角打分，选择得分最高的视角作为最优视角。
实施例
[0051]
本实施例中，如图4a、图4b、4c所示为输入的模型集合，通过本发明所述的三维模型最优视角选择方法，可以得到图5a、图5b、5c中每个三维模型的最优视角选择结果。具体实施过程如下：步骤1中，对已分类的三维模型集经过姿态校正和标准化分割后，得到姿态一致且同类模型分割标准一致的三维模型集合，模型分割结果如图2所示步骤2中，对每一类模型取出部分模型作为训练数据，通过包围模型的正20面体进行视角采样，采样结果如图3所示；通过采样所得的候选视角进行排序，作为标定的视角排序序列；对各训练模型的视角标定序列的首位视角对应的向量与模型竖直方向夹角的集合进行聚类，得到该类模型的最优视角角度；提取视角特征，并对特征赋予权重，通过设计函数来衡量一个视角的质量；通过粒子群优化算法来学习出权重函数中各类模型各特征的最优权重配置。
[0052]
步骤3中，对于已经过预处理的非训练模型，经过视角采样，提取特征，通过权重函数对各候选视角进行打分，得分最高的视角即选为最优视角，最优视角选择结果如图5a、图5b、5c所示。
[0053]
具体实现中，本技术提供计算机存储介质以及对应的数据处理单元，其中，该计算机存储介质能够存储计算机程序，所述计算机程序通过数据处理单元执行时可运行本发明提供的一种采用粒子群优化的三维模型最优视角选择方法的发明内容以及各实施例中的
部分或全部步骤。所述的存储介质可为磁碟、光盘、只读存储记忆体（read-only memory，rom）或随机存储记忆体（random access memory，ram）等。
[0054]
本领域的技术人员可以清楚地了解到本发明实施例中的技术方案可借助计算机程序以及其对应的通用硬件平台的方式来实现。基于这样的理解，本发明实施例中的技术方案本质上或者说对现有技术做出贡献的部分可以以计算机程序即软件产品的形式体现出来，该计算机程序软件产品可以存储在存储介质中，包括若干指令用以使得一台包含数据处理单元的设备（可以是个人计算机，服务器，单片机。muu或者网络设备等）执行本发明各个实施例或者实施例的某些部分所述的方法。
[0055]
本发明提供了一种采用粒子群优化的三维模型最优视角选择方法，具体实现该技术方案的方法和途径很多，以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。本实施例中未明确的各组成部分均可用现有技术加以实现。