复杂构型下的曲面生成方法与流程

1.本发明属于曲面建模设计技术领域，涉及一种复杂构型下的曲面生成方法，尤其是一种基于离散极小曲面原理的复杂构型下的曲面生成方法。


背景技术：

2.曲面建模是非常重要的一个领域，在工业界得到了广泛的应用。
3.极小曲面的含义是用两根铁丝各围成一个边界，将这两个边界放在肥皂水里面，将这两个边界同时取出来，由于水的表面张力的作用，所得到的曲面表面应当是最小的。在这种情况下，固定曲面边界所包围的曲面的面积最小，我们称其为极小曲面。极小曲面的平均曲率为0。
4.传统的曲面建模方法是先构建骨架曲线，之后通过放样、扫掠的方法得到曲面。在实际的操作过程中，曲面建模要求边界曲线尽可能简单，并且曲线本身的光滑性较高。此外，采用这种方法进行创建曲面时，要求曲线的曲率半径尽可能大，否则容易造成自相交的问题。采用这种方法的缺点主要是生成曲面的步骤繁琐，并且很难参数化，因此，需要大量人工干预。


技术实现要素：

5.本发明旨在至少解决现有技术中存在的技术问题之一。
6.为此，本发明提供了一种复杂构型下的曲面生成方法。
7.本发明的技术解决方案如下：
8.根据一方面，提供一种复杂构型下的曲面生成方法，该方法包括：
9.导入封闭曲线；
10.沿封闭曲线周向将任意所述封闭曲线进行离散化处理以得到多个线段；
11.基于所述多个线段构建三角形网格；
12.构建三角形网格对应的调和能量函数；
13.以所述封闭曲线作为边界约束，获取所述调和能量函数在单连通区域内部的分布以得到离散极小曲面。
14.进一步地，所述基于多个线段构建三角形网格，包括：
15.在离散化之后的封闭曲线所包围的内部区域添加一个点；
16.基于该点与多个线段构建三角形网格，其中，该点与任意线段构成一三角形网格单元。
17.进一步地，通过下式根据基于三角形网格的空间坐标构建调和能量函数e(f)：
18.[0019][0020]
其中，m代表布满三角形网格的曲面；vi代表曲面m上任何一个三角形的某一个顶点；j＝in,n＝1,2,3,4,......，vj代表顶点vi周围与该顶点连接的三角形的顶点；f代表三角形网格单元三维欧氏空间的坐标x,y,z，w
ij
是每个三角形的边长的权重因子，分别为顶点vi与顶点vj的连线所对应的两个三角形的顶角。
[0021]
进一步地，获取所述调和能量函数在单连通区域内部的分布以得到离散极小曲面，包括：
[0022]
根据所述调和能量函数，通过最小化调和能量值，得到下述方程(1)：
[0023][0024]
以封闭曲线为边界约束，求解方程(1)即得到调和函数在单连通区域内部的分布。
[0025]
进一步地，所述方法还包括：采用delaunay算法将构建的所述三角形网格进行重新划分以得到新的三角形网格，相应的，所述方法中，在构建调和能量函数时，构建所述新的三角形网格对应的调和能量函数。
[0026]
根据另一方面，提供一种计算机设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述的曲面生成方法。
[0027]
应用上述技术方案，通过对封闭曲线进行离散化处理以构建三角形网格，并根据三角形网格的空间坐标构建调和能量函数，依次获得曲线对应的极小曲面，由此，实现了在较少计算量的前提下，根据封闭的边界，自动化生成生成单连通曲面，实现了复杂构型的高质量曲面的生成，同时可以保证曲面本身的光顺性。
附图说明
[0028]
所包括的附图用来提供对本发明实施例的进一步的理解，其构成了说明书的一部分，用于例示本发明的实施例，并与文字描述一起来阐释本发明的原理。显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0029]
图1为本发明实施例提供的在封闭曲线所包围区域内添加一点后得到的初始曲面的各个单元的外观图；
[0030]
图2为本发明实施例提供的单连通区域经过重新划分之后所得到的三角形网格分布图；
[0031]
图3为本发明实施例提供的角度示意图；
[0032]
图4为本发明实施例提供的初始曲面与迭代之后曲面的相互位置关系示意图；
[0033]
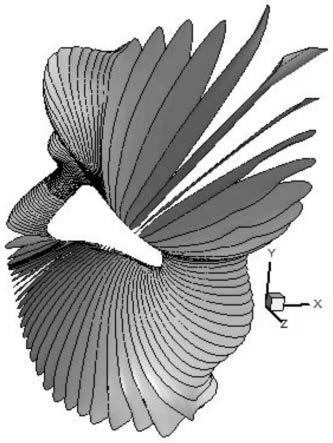
图5为本发明实施例提供的猫的构型的各个截面(即设计好的曲面)的集群；
[0034]
图6为本发明实施例提供的三角形网格局部示意图。
具体实施方式
[0035]
需要说明的是，在不冲突的情况下，本技术中的实施例及实施例中的特征可以相互组合。下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。以下对至少一个示例性实施例的描述实际上仅仅是说明性的，决不作为对本发明及其应用或使用的任何限制。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0036]
需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本技术的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。
[0037]
除非另外具体说明，否则在这些实施例中阐述的部件和步骤的相对布置、数字表达式和数值不限制本发明的范围。同时，应当明白，为了便于描述，附图中所示出的各个部分的尺寸并不是按照实际的比例关系绘制的。对于相关领域普通技术人员已知的技术、方法和设备可能不作详细讨论，但在适当情况下，所述技术、方法和设备应当被视为授权说明书的一部分。在这里示出和讨论的所有示例中，任何具体值应被解释为仅仅是示例性的，而不是作为限制。因此，示例性实施例的其它示例可以具有不同的值。应注意到：相似的标号和字母在下面的附图中表示类似项，因此，一旦某一项在一个附图中被定义，则在随后的附图中不需要对其进行进一步讨论。
[0038]
如图1-6所示，在本发明的一个实施例中，提供一种复杂构型下的曲面生成方法，该方法包括：
[0039]
s10、导入封闭曲线；
[0040]
s20、沿封闭曲线周向将任意所述封闭曲线进行离散化处理以得到多个线段；
[0041]
s30、基于所述多个线段构建三角形网格；
[0042]
s40、构建三角形网格对应的调和能量函数；
[0043]
s50、以所述封闭曲线作为边界约束，获取所述调和能量函数在单连通区域内部的分布以得到离散极小曲面。
[0044]
本发明实施例中，获取复杂构型表面上的多个封闭曲线为本领域常规技术手段，在此不再详细赘述。
[0045]
本发明实施例中，将封闭曲线进行离散化，也就是将其剖分为多个线段，目前，有很多种成熟方法构建封闭曲线的剖分方法，例如等参数分割法或者等线长分割方法；如图1所示，在本示例中，将边界剖分为144条线段。
[0046]
可见，本发明实施例将极小曲面其应用在构建光滑曲面的应用场景中。在具体操作和实践上，通过类似于调和映照的计算方法构建出离散极小曲面。
[0047]
应用上述配置方式，通过对封闭曲线进行离散化处理以构建三角形网格，并根据三角形网格的空间坐标构建调和能量函数，依次获得曲线对应的极小曲面，由此，实现了在较少计算量的前提下，根据封闭的边界，自动化生成生成单连通曲面，实现了复杂构型的高质量曲面的生成，同时可以保证曲面本身的光顺性。
[0048]
在上述实施例中，所述基于多个线段构建三角形网格，包括：
[0049]
在离散化之后的封闭曲线所包围的内部区域添加一个点；
[0050]
基于该点与多个线段构建三角形网格，其中，该点与任意线段构成一三角形网格单元。
[0051]
也即，在离散化之后的曲线所包围的内部区域，添加一个点，将该点与每一条线段的两端连接，即构成一个三角形网格单元，在本示例中，如图1所示，共有144个网格单元，每个单元就是一个三角形。
[0052]
在上述实施例中，所述方法在步骤s203之前还包括：采用delaunay算法将构建的所述三角形网格进行重新划分以得到新的三角形网格，相应的，所述方法中，在构建调和能量函数时，构建所述新的三角形网格对应的调和能量函数。
[0053]
也即，使用嵌入在三维欧氏空间的曲面上剖分delaunay的方法(对于平面delaunay三角剖分，我们可以认为每个三角形画一个外接圆，而外接圆的内部不包含三角剖分的任何顶点，这意味着可以用空外接圆的性质来定义delaunay三角剖分)，将图1所示的曲面进行三角形网格的重新划分，计算结果如图2所示。通过此种处理，能够将使得本实施例的有限元计算的结果更加准确，并且缩短计算迭代时间。
[0054]
在上述实施例中，如图6所示，可通过下式构建三角形网格对应的调和能量函数e(f)：
[0055][0056][0057]
其中，m代表布满三角形网格的曲面；vi代表曲面m上任何一个三角形的某一个顶点；j＝in,n＝1,2,3,4,......，vj代表顶点vi周围与该顶点连接的三角形的顶点；f代表三角形网格单元三维欧氏空间的坐标x,y,z，w
ij
是每个三角形的边长的权重因子，分别为顶点vi与顶点vj的连线所对应的两个三角形的顶角。如图3所示，j＝i1时，那么分别为顶点vi与顶点v
i1
的连线所对应的两个三角形的顶角。
[0058]
也即，本发明实施例中，f(vi)＝x(vi)，对应的f(vj)＝x(vj)，同时，对于坐标y,z也是如此。
[0059]
在上述实施例中，获取所述调和能量函数在单连通区域内部的分布以得到离散极小曲面，包括：
[0060]
根据所述调和能量函数，通过最小化调和能量值，得到下述方程(1)：
[0061][0062]
以封闭曲线为边界约束，求解方程(1)即得到调和函数在单连通区域内部的分布。
[0063]
也即，求解方程(1)，可以得到调和函数在单连通区域内部的分布，由此得到离散极小曲面。本发明实时中的调和映照的迭代方法实现原理是：给定边界处的调和函数值(本实施例即为封闭曲线)，内部区域某一点的调和函数由包围该点的多个点的调和函数所共同决定。在计算时，封闭曲线即为边界条件，对于内部区域各点的调和函数值，则给定调和
函数f和g的初值，通过迭代计算，可以给出收敛后的最终结果，得到调和函数在单连通区域内部的分布。
[0064]
如图4所示，虚线显示出的是应用了delaunay加密算法得到的曲面上的网格分布图，并且将它作为计算离散极小曲面的初始曲面。实线显示出的是经过迭代之后所得到的离散极小曲面。应用这种方法，如图5所示，我们可以把构型猫上的144条离散的封闭曲线都计算出其所对应的封闭的离散极小曲面。
[0065]
其中，对于本发明实施例获取的单个的离散极小曲面，应用场景是汽车/飞行器表面的建模。
[0066]
根据另一实施例，还提供一种计算机设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述的曲面获取方法。
[0067]
可见，本发明提供的是一种封闭曲线所包围的单连通曲面的设计方法，通过求解调和映照方程，可以无需人工干预，自动得到离散极小曲面的构型。所得到的离散极小曲面具有c2光滑性。本设计方法将计算共形几何的思想引入到了曲面生成的过程中。采用该方法所完成的曲面，可以保证图案在各处的连贯性与匹配性。实现了复杂构型下的曲面生成，初步展示了该设计方法的可行性，为该种设计方法的参数化研究打下了基础。
[0068]
为了便于描述，在这里可以使用空间相对术语，如“在
……
之上”、“在
……
上方”、“在
……
上表面”、“上面的”等，用来描述如在图中所示的一个器件或特征与其他器件或特征的空间位置关系。应当理解的是，空间相对术语旨在包含除了器件在图中所描述的方位之外的在使用或操作中的不同方位。例如，如果附图中的器件被倒置，则描述为“在其他器件或构造上方”或“在其他器件或构造之上”的器件之后将被定位为“在其他器件或构造下方”或“在其他器件或构造之下”。因而，示例性术语“在
……
上方”可以包括“在
……
上方”和“在
……
下方”两种方位。该器件也可以其他不同方式定位(旋转90度或处于其他方位)，并且对这里所使用的空间相对描述作出相应解释。
[0069]
此外，需要说明的是，使用“第一”、“第二”等词语来限定零部件，仅仅是为了便于对相应零部件进行区别，如没有另行声明，上述词语并没有特殊含义，因此不能理解为对本发明保护范围的限制。
[0070]
以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。