有效载荷微波器件低气压放电阈值高效预测方法

1.本发明属于高功率微波器件的电磁仿真技术，特别是一种有效载荷微波器件低气压放电阈值高效预测方法。


背景技术：

2.随着空间技术水平的不断提高，一方面无线通信系统中的传输功率不断上升，工作带宽不断增加；另一方面广泛应用于遥感导航、雷达探测、卫星通信的微波电子器件结构日趋复杂。入射电场在不连续结构如狭缝、小孔、调谐螺母等处激增，带来了微波击穿气体放电的风险。近年来，高功率微波越来越接近背景气体的击穿阈值。一旦产生气体放电现象，有效载荷微波器件极易被损毁，伴随生成的等离子体对电磁波产生衰减作用，严重影响微波器件性能乃至整个微波设备的可靠性和安全性。因此针对有效载荷微波器件，使用数值方法对击穿阈值进行预测具有重要意义。
3.使用数值方法对高功率微波击穿阈值问题进行分析，具有突出的优势且十分必要。通过理论分析、数值仿真、实验测试三者相结合，可以对高功率微波击穿阈值问题进行系统的分析，从而揭示输运系数等参数对击穿阈值影响的规律。从实际应用的角度出发，对于测试难度较大的实验，通过数值仿真可以对结果进行预测，从而总结变化规律，由此可以缩短设计研发周期，节约实验成本。
4.为了准确预测击穿阈值，不同的数值模型和输运系数被采用。在文献1.c.q ian,d.z.ding,z.h.fan,and r.s.chen,“afluid model simulation ofa simplified plasma limiter based on spectral-element time-domain method,”physics of plasmas.,vol.22,pp.032111,2015，基于麦克斯韦和流体方程，利用自恰数值模型来讨论矩形波导结构高功率微波击穿特性。如文献2.i.medina,c.j.j.hern
á
ndez-g
ó
mez and d.saucedo-jim
é
nez,"on waveguide’s critical corona breakdown thresholds dependence on the collision frequency between electrons and air,"ieee transactions on plasma science,vol.47,no.3,pp.1611-1615,2019,提出了一种新的碰撞频率修正因子，以使波导结构的击穿阈值解析计算结果与实验结果接近。如文献3.u.jordan et al.,"on the effective diffusion length for microwave breakdown,"ieee transactions on plasma science,vol.34,no.2,pp.421-430,2006，使用有效扩散长度对波导结构微波击穿阈值进行预测。现有方法计算整个区域时效率较低，并且未考虑场分布对输运系数造成的影响，时域谱元法采用六面体单元离散网格，可以很好的描述器件的几何外形，采用具有正交性质的基函数测试展开，所生成的质量矩阵具有块对角性质，本征值求解速度较快，在分析高功率微波器件气体击穿阈值问题时具有较大优势。


技术实现要素：

5.本发明的目的在于提供一种有效载荷微波器件低气压放电阈值高效预测方法，实
现有效载荷微波器件击穿阈值的高效准确预测，能够在保证结果精度的条件下降低研发成本，为有效载荷高功率微波器件的设计提供指导。
6.实现本发明目的的技术解决方案为：一种有效载荷微波器件低气压放电阈值高效预测方法，包括步骤：
7.步骤一：根据有效载荷微波器件的复杂几何模型，采用曲六面体网格对目标进行离散，可以很好拟合目标外形，由电磁分析算法计算获得频域电场分布，根据场模值的最大值对场分布进行归一化处理；
8.步骤二：对电子连续性方程作单边laplace变换并添加电子密度相关边界条件，之后对变换后方程中的电子密度未知量利用基函数进行展开，基函数选用guass-lobatto-legendre基函数，再利用基函数作为加权函数对方程进行测试，得到半离散格式，对半离散格式中的矩阵对角化并作laplace反变换得到时域方程，最终将微波击穿阈值的预测问题转化为本征值求解问题；
9.步骤三：设置工作压强以及初始入射场强，根据入射波频率、输运系数中碰撞率以及步骤一中获取的归一化电场分布计算有效电场强度，通过有效电场强度计算当前电离率、附着率；
10.步骤四：根据场分布和设定的阈值选取场值变化剧烈的区域进行分析(场值大于设定阈值的为变化剧烈的区域)，截取所需计算区域并填充相应矩阵，矩阵本征值求解。
11.步骤五：重复步骤四的本征值求解过程，判断所求最小本征值与0的大小。当最小特征值大于0，采用二分法向范围上限更新入射场幅值，反之则向下限更新；
12.步骤六：若满足最终收敛判断依据，输出此时入射场强，并根据坡印廷定理进行功率幅值转换得到击穿时的端口入射功率。
13.进一步地，所述步骤二中，电子连续性方程可以表示为：
[0014][0015]
(1)式中n表示电子密度，vi表示电离率，va表示附着率，d表示扩散系数，d＝106/p，p为填充气体的压强。
[0016]
进一步地，对电子连续性方程作单边laplace变换可以得到：
[0017][0018]
对(2)式添加边界条件，边界处电子密度其中v表示体积。
[0019]
进一步地，对(2)式进行基函数展开以及伽辽金测试可以得到半离散格式方程，方程如下：
[0020][0021]
其中：
[0022]
[m]
ij
＝∫vψiψjdv
[0023][0024]
[n0]＝∫vψin0dv
[0025]
v为单元内的体积分区域，ψi、ψj分别为测试基与展开基，i、j非别为测试基与展开基的下标，m、k、n0为单元系数矩阵。
[0026]
进一步地，对(3)式进一步求解可以得到:
[0027][0028]
(4)式中i为单位阵。
[0029]
进一步地，对(5)式中m-1
k对角化可以得到:
[0030][0031]
(5)式中p为可逆矩阵，λi为特征值。
[0032]
进一步地，对(5)式进行laplace反变换可以得到时域方程:
[0033][0034]
进一步地，所述步骤三中，初始入射场强可以表示为:
[0035][0036]
(7)式中ea，eb表示设置初始入射电场强度的最小值和最大值。
[0037]
进一步地，电离率vi与附着率va可以表示为:
[0038][0039]
(8)式中a表示有效电场e
eff
与压强p的比值。
[0040]
进一步地，所述(8)式中a可表示为:
[0041][0042]
(9)式中e
eff
表示有效电场强度，ω表示入射波角频率，vc表示碰撞率，vc＝5
×
109p。结合以上输运系数进行本征值求解，当本征值趋向0时输出e0得到器件的击穿阈值。
[0043]
本发明与现有技术相比，其显著优点为：
[0044]
(1)本发明对决定微波器件击穿阈值与功率容量的电子连续性方程具有谱精度的谱元法进行求解，针对复杂目标引入有效电场强度和归一化场分布对输运系数进行修正，通过本征值求解可实现对器件的击穿阈值预测，缩短了实验周期和节约成本；
[0045]
(2)现有击穿阈值的预测方法大多针对规则波导模型，未考虑器件内部电磁场分布情况，本发明所提方法针对复杂目标模型，使用电磁分析算法计算获得器件内部电场分布，根据场模值的最大值对场分布进行归一化，相比无场分布的击穿阈值预测方法计算结果更加精确；
[0046]
(3)本发明所提方法为了提高复杂化目标击穿阈值分析的效率，使用区域分解方法选取较易击穿的区域进行分析，大大减少击穿阈值分析的未知量，极大地较少了复杂结构的微波器件击穿阈值的计算时间。
附图说明
[0047]
图1中的(a)为脊波导物理结构侧视图，图1中的(b)为脊波导物理结构正视图。
[0048]
图2是击穿阈值随压强变化规律图。
[0049]
图3是计算时间对比图。
[0050]
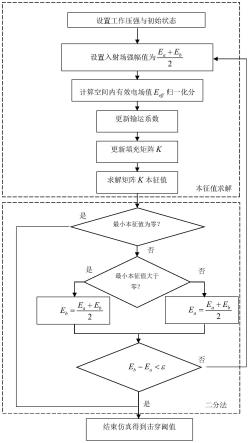
图4是本发明击穿阈值求解的流程图。
具体实施方式
[0051]
为了准确获取有效载荷微波器件的击穿阈值，本发明引入复杂目标的场分布来更新输运系数，采用区域分解技术选取较易击穿的区域进行分析以提高计算效率，最终实现有效载荷微波器件击穿阈值的高效准确预测，能够在保证结果精度的条件下降低研发成本，为有效载荷高功率微波器件的设计提供指导。下面结合附图，以图1所示脊波导结构为例，对本发明提出的有效载荷微波器件低气压放电阈值高效预测方法的具体步骤作进一步详细描述。
[0052]
参见图1所示脊波导结构示意图，模型几何尺寸如下：脊波导长边a＝44mm，短边b＝20.2mm，总长l＝174.4mm。根据本发明分析图1所示脊波导结构的高功率微波气体击穿阈值的数值仿真方法，结合图4，其具体操作步骤如下：
[0053]
第一步，根据图1所示脊波导结构的几何模型，首先使用ansys软件进行建模，采用曲六面体对其进行网格剖分，得到该结构的节点坐标信息以及单元信息，对于波导结构的边界条件，除传输方向端口外的四个面设置为理想金属，传输方向的端口采用一阶吸收边界，此外对激励源的位置进行设置，激励源为传输方向上的整个平面，模型采用中心频率f＝3.85ghz的正弦波作为激励源，并根据施加激励源计算器件内部的电场分布。
[0054]
第二步，针对决定微波器件击穿阈值与功率容量的电子连续性方程，作单边laplace变换，变换后添加有关电子密度的边界条件，然后采用时域谱元法对电子密度未知量进行展开，通过伽辽金测试将微分方程转换为矩阵方程组，方程组如下所示：
[0055][0056]
其中：
[0057]
[m]
ij
＝∫vψiψjdv
[0058][0059]
[n0]＝∫vψin0dv
[0060]
之后对矩阵方程作laplace反变换得到时域方程，方程如下所示：
[0061][0062]
由此可以将微波击穿阈值的预测问题转化为本征值求解问题。
[0063]
第三步，设置工作压强，初始入射场强，根据入射波频率、输运系数中碰撞率以及归一化电场分布计算有效电场强度，通过有效电场强度计算当前电离率、附着率，使用区域分解方法填充相应矩阵，之后进行矩阵本征值求解。其中初始入射场强、碰撞率、有效电场强度、电离率以及附着率的计算公式如下所示：
[0064][0065]
vc＝5
×
109p
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0066][0067]
vi＝5.14
×
10
11
pexp(-73a-0.44
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(15)
[0068]
va＝7.6
×
10-4
pa2(a+218)2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(16)
[0069]
第四步，根据场分布选取场值分布较大区域进行分析，截取所需计算区域并填充相应矩阵，对矩阵k进行本征值求解，具体如下所示：
[0070]
kn＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(17)
[0071]
其中
[0072]
第五步，根据第四步求出的本征值，当本征值大于0时器件未击穿，更新电场强度范围中最小值ea，当本征值小于0时器件击穿，更新电场强度范围中最大值eb。
[0073]
第六步，当所求最小本征值趋向为0或击穿阈值区间满足设定范围时停止循环，输出此时入射场强，并根据坡印廷定理进行功率幅值转换得到击穿时的端口入射功率，功率幅值转换如下所示：
[0074][0075]
其中s为加源端口横截面，z为波阻抗，e
t
为横向电场分量。
[0076]
根据本发明所述方法对图1所示s波段脊波导进行仿真，不同压强下的击穿阈值如图2所示，相较于未考虑场分布影响的传统方法，本发明所述方法更接近实验结果，精度更高。击穿阈值随着压强增大有一个先降低后升高的过程，满足帕邢规律。在小于5mbar部分，由于压强较低电子自由程较大，与中性粒子碰撞电离概率较小，粒子的扩散运动占主导地位，因此在该部分随着压强增大电离率增加，击穿阈值减小。在大于5mbar部分，附着率开始占据主导地位，此时电子以团簇形式存在，因此需要更大的场强才能产生微波击穿现象。图3为本发明所提方法与整体分析的计算时间对比，由于谱元法所生成的质量矩阵具有块对角性质，矩阵本征值求解速度较快，同时结合区域分解方法降低计算未知量，因此计算时间能够大大减少。