一种适用于任意初始含水量分布下的边坡降雨入渗-径流计算方法

本发明涉及到一种适用于任意初始含水量分布下的边坡降雨入渗-径流计算方法，属于土壤物理和山坡水文学。

背景技术：

1、降雨滴落至土壤表层时，会入渗进入土壤，直到降雨强度超过土壤有限的入渗能力，此时土壤表层产生积水，径流和侵蚀也随之发生。准确的估计积水发生时间以及径流产生量对于水文预报、农业灌溉设计、水土保持至关重要。

2、降雨入渗是一个复杂的动态过程，主要的影响因素包括降雨强度随时间的变化、土壤剖面的水力特性参数、剖面上初始含水量的分布状态以及坡度等。当前主要采用有限元和有限差分法数值求解richards方程来估计积水发生时间和径流产生量，但数值模拟方法往往需要在时间和空间上进行高度的离散化来适应上边界复杂的降雨强度变化。此外求解一个高度非线性的richards方程需要消耗大量的算力，因此这类方法的模拟过程往往面临着数值运算不稳定、计算成本较高等问题。作为一种改进方法，经验、解析、半解析的入渗方程因其形式简单，不需要时空离散化，和保证了水量平衡而被发现，并应用于入渗-径流过程的模拟。但由于降雨入渗问题的复杂性，现存的入渗方程要么忽略了降雨强度随时间变化这一自然特征(cn 105547957；cn 112685874；cn 109898489)，亦或是本身具有的初始含水量均匀分布的假定无法满足田间初始含水量呈非均匀分布的条件(chen and young,2006；wang et.al,2018),均难以真正应用于真实的野外环境。故目前仍缺乏一种可在野外使用的，能够模拟非稳态降雨下初始含水量呈非均匀分布的边坡入渗-径流计算方法，这将极大地降低水文预报的时效性与准确性。

技术实现思路

1、本发明的目的是克服现有技术的不足，提供一种适用于任意初始含水量分布下的边坡降雨入渗-径流计算方法。

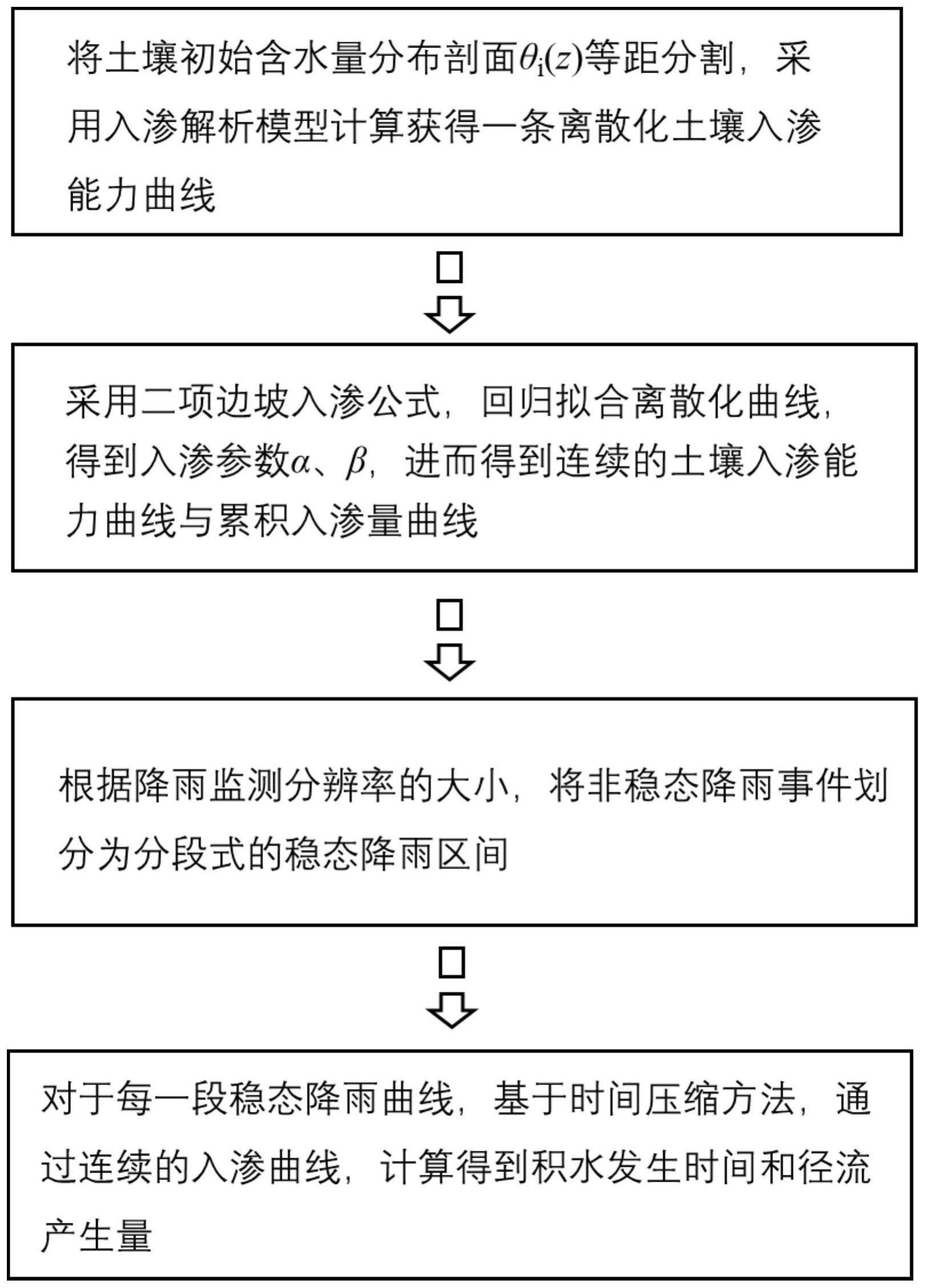
2、本计算方法所预先需要测定的模型参数包括：1、土壤的初始含水量分布剖面θi(z)；2、brooks-corey模型描述的土壤水力学参数n、hd，土壤的饱和导水率ks，和饱和含水量θs。具体计算方法的步骤包括：

3、步骤1，对于已知的将土壤的初始含水量分布剖面θs-θi(z)分割成n个等宽的长条形，取每个条形的中心点作为该分割的标志点ξj，则

4、

5、

6、式中，zmax是已知土壤水分剖面的最大深度；z0、z1分别是第1个等宽长条形的上端和下端在土壤水分剖面中所处的位置；zn是第n个等宽长条形的下端在土壤水分剖面中所处的位置；

7、步骤2，根据步骤1的分割剖面，土壤累积入渗量i被表示为黎曼和的形式：

8、

9、式(13)中，jw0(zfe＝ξj)是当虚拟的活塞型的湿润区长度zfe到达标志点ξj时的表层土壤入渗率；△tj和△ij分别是zfe经历△zj距离时所需的时间以及增加的入渗量；θi(ξj)是土壤水分剖面深度z＝ξj处的初始土壤含水量。

10、利用一阶泰勒级数展开式和中心差分方法，θi(ξj)和jw0(zfe＝ξj)被表示为：

11、

12、

13、结合公式(13)和公式(14)计算得到δij(j＝1,2,···n)，计算表达式为：

14、

15、对于已知的δij(j＝1,2,···n)，结合公式(13)与公式(15)，计算得到△tj(j＝2,···n)，计算表达式为：

16、

17、对于已知的δtj(j＝1,2,···n)，zfe到达一个确定的土壤水分剖面深度zj所用时间按照如下公式计算，

18、

19、进而，对于给定的土壤的初始含水量分布剖面θs-θi(z)，可以计算得到了一条离散的土壤入渗能力曲线jw0(zfe)～t(zfe)；

20、步骤3，对于步骤2所得到的离散的土壤入渗能力曲线，采用philip二项边坡入渗公式进行参数α、β的拟合，进而获得一条连续的表层土壤入渗率曲线jw0(t)，

21、jw0＝αtβ+ks cosγ    (20)

22、式中，γ为坡度，根据质量守恒原理，一条连续的累积入渗量曲线i(t)表示为，

23、

24、步骤4，根据降雨监测分辨率的大小，将非稳态降雨事件划分为分段式的稳态降雨区间，在第n段稳态降雨区间内的降雨速率rn(t)＝rncosγ可以被表示为，

25、rn(t)＝[r(tn)-r(tn-1)]/(tn-tn-1)＝[r(tn)-r(tn-1)]/δtn＝rn cosγ    (26)

26、式中，tn与tn-1分别是第n段和第n-1段末的降雨历时，r(tn)与r(tn-1)分别是第n段和第n-1段末的累积降雨量；δtn为第n段的降雨区间时长；

27、步骤5，对于第一段稳态降雨，降雨速率为r1cosγ，区间内的积水时间tp、虚拟时间ts以及稳态降雨下产生积水时的累积入渗量ip通过下式被计算，

28、

29、

30、

31、此时的土壤入渗能力通过如下公式描述，

32、jw0＝α[t-(tp-ts)]β+ks cosγ     (22)

33、累积入渗量i(t1)通过公式(21)与下式联立计算获得，

34、i(t1)＝tpr1cosγ+i(ts+δt1-tp)-i(ts)     (27)

35、累积径流量f(t1)被表示为，

36、f(t1)＝δt1r1cosγ-i(t1)     (28)；

37、步骤6，基于时间压缩方法，计算第n-1段末(n>2)的土壤入渗能力jw0(tsn-1)，

38、i[jw0(tsn-1)]＝i(tn-1)        (29)式中，i(tn-1)为在n-1段稳态降雨区间末的土壤累积入渗量；

39、步骤7，根据比较土壤入渗能力jw0(tsn-1)与降雨速率rncosγ的大小，确定在第n段稳态降雨区间内，积水发生的时间以及径流产生量；

40、a).当jw0(tsn-1)≤rncosγ时，表明在第n段稳态降雨区间内，积水会瞬时发生或继续维持，此时的土壤入渗能力通过公式(22)描述，tp＝tn-1，ts＝tsn-1，累积入渗量i(tn)通过下式计算：

41、i(tn)＝i(tn-1)+i(tsn-1+δtn)-i(tsn-1)     (31)

42、累积径流量f(tn)通过下式计算：

43、f(tn)＝δtnrn cosγ-i(tn)+f(tn-1)     (32)

44、b).当jw0(tsn-1)＞rncosγ时，表明在第n段稳态降雨区间，积水不会瞬时发生，在第n段稳态降雨区间内的积水时间tpn通过下式计算：

45、rn cosγ＝jw0[i(tn-1)+rn cosγtpn]    (33)

46、如果tpn≥δtn，表明该区间并不产生积水，则此时的累积入渗量i(tn)和累积径流量f(tn)被分别表示为：

47、i(tn)＝i(tn-1)+rn cosγδtn                 (35)

48、f(tn)＝δtnrn cosγ+f(tn-1)                (36)

49、相反的，如果tpn＜δtn，此时的土壤入渗能力通过下式描述(tp＝tn-1+tpn)

50、jw0＝α[t-(tp-ts)]β+ks cosγ   (22)

51、累积入渗量i(tn)和累积径流量f(tn)被分别表示为：

52、i(tn)＝i(tn-1)+tpnrn cosγ+i(tsn-1+δtn-tpn)-i(tsn-1)             (37)

53、f(tn)＝δtnrn cosγ-i(tn)+f(tn-1)           (38)。

54、作为本发明的一种优选技术方案：所述步骤2中，公式(17)中的jw0(zfe＝zj)首先按以下公式：

55、

56、执行不动点迭代，获得湿润区中饱和区所占的长度zfw(cm)，将zfw代入以下公式，

57、

58、获得jw0(zfe＝zj)；

59、式中未知参数的定义如下：

60、

61、作为本发明的一种优选技术方案：所述步骤2中，由于在入渗的初始时刻，公式(17)中表层土壤入渗率jw0(zfe＝z0)是无穷大的，因此δt1单独通过以下公式计算，式中初始含水量θi＝[θi(z0)+θi(z1)]/2，t＝δt1以及jw0＝jw0(zfe＝z1)，

62、

63、式中，δh＝hf+hd＝-ηhd；其余参数定义同上。

64、作为本发明的一种优选技术方案：所述步骤6中，根据土壤的饱和导水率ks以及入渗参数α、β，按如下公式：

65、

66、执行不动点迭代算法获得第n-1段的降雨区间末的虚拟时间tsn-1(min)，将tsn-1代入公式(20)，计算得到jw0(tsn-1)。

67、作为本发明的一种优选技术方案：所述步骤7中，将公式(32)代入公式(21)中，联立计算得到公式：

68、

69、将上式中的i替换为i(tn-1)+rncosγtpn，jw0替换为rncosγ，进行不动点迭代算法，计算获得tpn。

70、作为本发明的一种优选技术方案：所述步骤7中，公式(22)中的参数ts采用以下公式计算，

71、

72、作为本发明的一种优选技术方案：所述步骤1中，n值至少在101以上。

73、本发明的有益效果如下：

74、1、与已有技术相比，本发明考虑了降雨强度的非稳态性、土壤初始含水量呈非均匀分布等野外真实条件，基于积水条件下的边坡入渗方程，一种可以模拟任意初始含水量分布条件下的降雨入渗解析计算方法被提出，准确估计了均质土的积水发生时间与径流产生量，这为水文预报、农业灌溉设计、水土保持等领域提供了一个有效的计算工具；

75、2、计算方法简单。本发明仅需已知待计算土壤剖面的水力学性质、土壤初始含水量的分布以及上边界的降雨强度随时间的变化数据，便可计算得出积水发生时间与径流产生量，其计算过程不需要进行复杂的时间与空间的离散化，计算稳定、快速，且保证水量平衡，是一种简单，准确的计算方法。