基于迁移学习的多模式流程工业过程的数据驱动故障检测方法

1.本发明涉及流程工业过程故障检测技术领域，特别涉及一种基于迁移学习的多模式流程工业过程的数据驱动故障检测方法。


背景技术：

2.故障检测对于复杂工业系统的安全运行至关重要。基于数据驱动的故障检测方法相比基于知识和解析模型的方法具有建模过程简单、无需复杂机理建模等优点。因此，关于数据驱动故障检测方法的研究和应用正在广泛地开展。其中，基于多元统计的方法受到越来越多的关注。然而，这些方法都需要大量的历史数据来建立模型。但是，在实际生产过程中，某些流程工业过程无法获得大量的历史数据。比如一座未正式投入使用的新的污水处理厂，它的可获取的历史数据很少。虽然旧的污水处理厂有着大量的历史数据，但是旧的污水处理厂的历史数据不能直接作为新的污水处理厂的历史数据，否则会导致用于模型训练和测试的数据来自不同的分布，从而使建立的系统模型的性能下降。这是因为新的和旧的污水处理厂的工艺参数不同，它们在相同模式下收集的数据的分布会有差异。除此之外，流程工业过程还具有多模式、非线性的特点。传统的基于多元统计的方法大多只适用于线性假设的情况，大多建立的是单模式的系统模型。
3.综上所述，基于数据驱动的故障检测方法大部分依赖于足够的历史数据，并且要求用于模型训练和测试的数据通常来自相同的分布，对于一些实际的流程工业过程来说，这些条件难以满足。除此之外，工业过程数据还表现出非线性的特点，基于多元统计的故障检测方法大多只适用于线性假设的情况，不能处理非线性的情况。当系统呈现出非线性的特点时，传统的基于多元统计的方法很难建立起准确的系统模型。此外，流程工业过程数据还呈现出多模式的特点，这使得系统模型在监测故障时，要能区分模式变化和故障变化，避免系统错误地将模式变化判断为故障。在大多数的数据驱动的故障检测方法中，这个问题并没有被考虑到。


技术实现要素：

4.本发明的目的在于提供一种基于迁移学习的多模式流程工业过程的数据驱动故障检测方法，针对多模式的流程工业过程，在没有足够历史数据的情况下，或者用于模型训练和测试的数据来自不同的分布时，通过迁移学习技术来建立系统的故障检测模型，解决目标对象无法建模的问题；针对多模式的流程工业过程，在系统呈现出非线性的特点时，利用基于张量分解的核函数处理非线性数据，通过基于典型多元分解的子空间分离的技术解决多模式系统建模的问题，降低了建模成本，提高了系统检测效率；针对多模式的流程工业过程，通过协积分分析建立系统的动态平稳监测模型来区分模式变化和故障变化，避免系统错误地将模式变化判断为故障，提高了系统检测的准确率。
5.为解决上述技术问题，本发明的实施例提供如下方案：
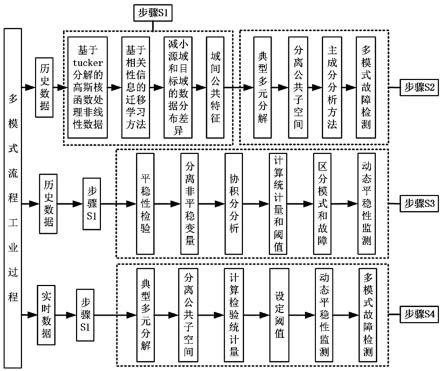
一种基于迁移学习的多模式流程工业过程的数据驱动故障检测方法，包括以下步骤：s1，采集流程工业过程的历史数据；利用基于tucker分解的高斯核函数处理非线性数据，然后基于相关性信息的迁移学习方法减小源域和目标域数据分布的差异，获得域间共享特征；s2，根据域间共享特征，基于典型多元分解和主成分分析建立流程工业过程的多模式故障检测模型；s3，根据域间共享特征，进行平稳性检验分离非平稳变量，利用协积分分析建立非平稳变量的动态平稳监测模型，最终建立一套完整的多模式流程工业过程故障检测模型；s4，利用建立好的多模式流程工业过程故障检测模型，应用于多模式流程工业过程的在线故障检测。
6.优选地，所述步骤s1具体包括以下步骤：s11，采集流程工业过程的历史数据；这里的流程工业过程指污水处理过程，采集的历史数据反映污水处理过程的运行状况，形成污水处理数据的数据集；采集的数据集包括作为源域的第一污水处理厂的数据和作为目标域的第二污水处理厂的数据；s12，利用步骤s11采集的数据集作为训练数据，利用基于tucker分解的高斯核函数处理非线性数据；根据tucker分解的定义，一个n阶张量x表示为如下的关于因子矩阵列向量外积的形式：其中，x是一个n阶张量，n表示张量的阶数，g是核张量，是因子矩阵，这里；表示指标集，表示核张量g在各个阶数上的维度大小，表示核张量g在各个阶数上的分量，表示各个因子矩阵的列向量；根据核函数映射理论，对已有的tucker分解式作如下的变换：其中，表示一个核映射，表示的高维核映射，表示的高维核映射；假设x，y为原始空间的张量，对它们进行tucker分解：
其中，x是一个n阶张量，n表示张量的阶数，表示张量x的因子矩阵的列向量；y是一个n阶张量，表示指标集，表示张量y的核张量在各个阶数上的维度大小，表示张量y的核张量在各个阶数上的分量，表示张量y的因子矩阵的列向量；在高维的特征空间中，核函数由两个高维元素的内积运算表示：其中，表示由张量x和张量y构成的核函数，表示张量x的高维核映射，表示张量y的高维核映射，表示的高维核映射，表示的高维核映射，表示的高维核映射，表示的高维核映射，表示高斯核函数；选择高斯核函数作为基础核函数，得到基于tucker分解的高斯核函数为：其中，是高斯核函数中的控制参数，用于设置带宽，通过优化搜索算法找到最优值；s13，利用基于相关性信息的迁移学习方法减小源域和目标域数据分布的差异，获得域间共享特征；设有源域和目标域，假设源域数据是个模式的多模过程，目标域数据也是个模式
的多模过程，其中，和分别表示源域数据样本和目标域数据样本的数量，表示数据样本的变量数，表示维的实数空间，表示维的实数空间；则有：其中，表示数据样本的变量数，表示源域第个模式的数据，表示源域第个模式数据矩阵的第个列向量，表示目标域第个模式的数据，表示目标域第个模式数据矩阵的第个列向量；在高维特征空间中，源域的每个模式的数据表示为：其中，表示一个核映射，表示的高维映射，表示的高维映射；源域的第个模式的协方差矩阵为：其中，表示源域第个模式的数据矩阵的行向量，表示的高维映射；的主要特征通过寻找协方差矩阵的特征向量来求解：其中表示点乘，表示特征值，是源域协方差矩阵的特征向量；当时，的主要特征表示为：其中，是一组系数；同理，目标域第个模式的数据的高维映射为，它的主要特征为：
其中，是一组系数，表示目标域第个模式的数据矩阵的行向量，表示的高维映射，是目标域协方差矩阵的特征向量；利用核技巧，得到：其中，表示源域的非中心核矩阵，表示源域第个模式的系数因子矩阵，源域第个模式的所有的特征值都按照从大到小的形式排列，其相应的系数因子向量为，保留前个特征值，即保留前个系数因子向量；基于相似性理论，将特征向量的比较转化为系数因子的比较，求特征向量对应的得分转化为求相应系数因子对应的得分；中心核矩阵是使用非中心核矩阵计算得到的：其中，表示全为的阶方阵，它是核矩阵中心化的辅助矩阵；因此，得到：其中，表示源域第个模式的内核主成分矩阵的列向量，表示源域第个模式的协方差矩阵的特征向量，表示源域第个模式的系数因子矩阵的元素，表示中心核矩阵的函数，表示源域第个模式的数据，表示源域第个模式数据矩阵的行向量，表示的高维映射，表示保留的前个特征值，即降维后的维数，；源域的第个模式的内核主成分矩阵为：
其中，表示源域第个模式的内核主成分矩阵的列向量；同理，目标域的第个模式的内核主成分矩阵为：其中，表示目标域第个模式的内核主成分矩阵的列向量；源域的第个模式的系数因子矩阵表示为：同理，目标域的第个模式的系数因子矩阵表示为：其中，表示的列向量，表示的列向量；源域和目标域系数因子的相关性为：目标是寻求函数所有大于0.6的因子组合；然后假设其中一组为特征中心；在源域中，根据典型相关分析，源域在特征中心上的特征为：其中，表示源域在特征中心上的特征，表示源域数据与特征中心的相关性矩阵，表示的转置，表示源域的第个模式的内核主成分矩阵；同理，目标域在特征中心上的特征为：其中，表示目标域在特征中心上的特征，表示目标域数据与特征中心的相关性矩阵，表示目标域的第个模式的内核主成分矩阵；s14，源域数据和目标域数据之间最大平均差异距离越小，说明数据分布差异越小，因此有以下目标函数：
其中，mmd表示最大平均差异距离，表示最大平均差异距离矩阵，表示最大平均差异距离矩阵中的元素，和表示源域和目标域中内核主成分矩阵的行向量；表示源域第个模式的数据矩阵的行向量，表示源域的内核主成分矩阵的行向量，表示目标域第个模式的数据矩阵的行向量，表示目标域的内核主成分矩阵的行向量，表示矩阵的迹，，。
7.优选地，所述步骤s2具体包括以下步骤：s21，假设经过数据预处理的污水处理过程的数据为，它是个模式的多模过程，其中，表示样本数，表示变量数，表示维的实数空间；则有：其中，表示第个模式的数据，表示的第个列向量；对于第个模式的数据来说，它构成了一个测量空间；测量空间被划分为公共子空间和特殊子空间，表示为：
其中，表示模式间共享的公共子空间，表示每个模式的特殊子空间；基于以上分析，有下面这个框架：其中，表示第个模式的特征，表示第个模式的得分矩阵，表示模式内的公共特征，表示第个模式的特殊特征，表示模式内的得分矩阵，表示第个模式的特殊得分矩阵；s22，通过前面的分析，得到源域和目标域之间每个模式的共享信息为；按照张量的mode-1展开式的形式排列，被组合成一个新的三阶张量，张量沿mode-n展开成一个矩阵；张量的mode-1展开式为：其中，是样本数，是变量数，是模式数，表示维的实数空间；假设张量构成的测量空间为，根据前面的分析，测量空间被划分为公共子空间和特殊子空间，表示为：s23，典型多元分解将一个张量分解成分量张量的和；对于一个秩为h的三阶张量，张量的典型多元分解表示为：其中，表示张量典型多元分解后的因子矩阵，表示因子矩阵的列向量；令，典型多元分解以矩阵化的形式写成：
其中，表示张量的mode-1展开式，表示张量的mode-2展开式，表示张量的mode-3展开式；利用交替最小二乘法计算出矩阵t、p、c，公共子空间被定义为：其中，，，表示因子矩阵第个模式方向的切片，表示切片的对角阵；s24，秩h由张量分解的距离差公式确定；假设经过典型多元分解之后，逆运算得到重构张量；张量分解的距离差的计算公式为：其中，f表示f范数；不同的秩h，距离差不同，当距离差最小时，此时的秩h即为所求；s25，在找出公共子空间后，直接计算每个模式的左侧部分，特殊子空间为：仿照主成分分析的方法，得到的特殊特征，所以有：其中，是的得分矩阵。
8.优选地，所述步骤s3具体包括以下步骤：s31，首先对源域数据进行tucker分解高斯核的非线性处理，然后利用相关性信息的迁移学习方法映射到域共享空间，得到新的域间共享特征；此时，根据建立目标域的动态平稳监测模型；选取的若干组单变量的数据，进行平稳性检验；根据先验知识和平稳性检验，分离出非平稳变量；将具有共同趋势的非平稳变量，标记为；s32，给定非平稳时间序列，对数据做归一化处理；利用johansen多变量协整分析方法对选取的数据进行协整关系检验，通过特征值分解求解协积分矩阵的最大似然估计，最终计算协积分矩阵。
9.优选地，所述步骤s4具体包括以下步骤：s41，多模式非线性系统的故障检测；在线采集到的第个模式的新样本为，数据做归一化处理，然后利用tucker分解高斯核处理非线性数据，利用基于相关性信息的迁移学习方法映射到域共享空
间，得到新的数据矩阵；将第个模式的新样本替换掉原来数据里的第个模式的数据，同时保持其他模式的数据不变；然后，组成一个新的张量，将这个张量沿着mode-1方向展开得到；因此，新的公共子空间的得分矩阵为：其中，p，c表示张量的典型多元分解后的因子矩阵；新的公共子空间被表示为：其中， ，，表示因子矩阵第个模式方向的切片，表示切片的对角阵；新的特殊子空间被表示为：新的特殊子空间的得分矩阵被表示为：其中，表示新的特殊特征；因此，新的特殊子空间被重新计算为：最后，剩余部分被计算为：最后，剩余部分被计算为：统计量是变量在主子空间中的投影大小，反映了每个变量的变化量，和分别用于监控公共子空间和特殊子空间的统计量，数学表达式是：分别用于监控公共子空间和特殊子空间的统计量，数学表达式是：的控制限表示为：
其中，表示f分布的临界值，自由度为，，置信水平为，表示样本数，表示保留的前个特征值，即降维后的维数，也是原始数据的内核主元的个数；统计量反映了数据样本在剩余子空间中的投影变化，即：统计量反映了数据样本在剩余子空间中的投影变化，即：的控制限表示为：式中，；表示数据样本协方差矩阵的第i个特征值，表示置信度下的标准正态分布的阈值；如果大于阈值，则发生的故障影响了共同特征；如果只有或大于它们的阈值，则发生的故障只影响了该模式下的特殊特征；s42，多模式非线性系统的动态平稳关系监测；在线采集到的第个模式的新样本为，数据做归一化处理，然后进行tucker分解高斯核的非线性处理，利用基于相关性信息的迁移学习方法映射到域共享空间，得到新的数据矩阵；在时刻，分离出非平稳变量，系统长期的动态平稳关系表示为：其中e为反映了长期动态平稳关系的误差，为第个时刻的协积分矩阵；因此，监测统计量表示为：表示为：的控制限表示为：
其中，和分别为的均值和方差，表示卡方分布，和是参数，置信水平为；当模式切换时，动态平稳关系被破坏，曲线波动后能恢复正常，统计量的值低于阈值；当故障发生时，动态平稳关系被破坏，曲线波动后不能恢复正常，统计量的值高于阈值。
10.本发明实施例提供的技术方案带来的有益效果至少包括：1）在实际流程工业过程中集成了迁移学习和故障检测技术，通过基于相关性信息的迁移学习方法解决了系统建模时历史数据不足的问题，解决了目标对象无法建模的问题，能够减少目标对象建模的成本。
11.2）针对多模式的流程工业过程，利用基于tucker分解的高斯核函数处理了非线性数据，解决了系统的非线性问题；通过基于典型多元分解的子空间分离的技术解决了多模式过程建模的问题，降低了建模成本，提高了系统的检测效率。
12.3）在故障检测的过程中，系统可以自主判断当前的扭曲变化属于模式变化还是故障变化；通过协积分分析技术建立系统的动态平稳监测模型，来区分模式变化和故障变化，避免系统错误地将模式变化判断为故障，提高了系统检测的准确率。
附图说明
13.为了更清楚地说明本发明实施例中的技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
14.图1是本发明实施例提供的基于迁移学习的多模式流程工业过程的数据驱动故障检测方法的流程图；图2是本发明实施例提供的污水处理模型示意图；图3a、图3b、图3c是本发明实施例提供的第一种情况下晴天公共空间统计量、晴天特殊子空间统计量、晴天特殊子空间统计量变化图；图4a、图4b、图4c是本发明实施例提供的第二种情况下晴天公共空间统计量、晴天特殊子空间统计量、晴天特殊子空间统计量变化图；图5a、图5b、图5c是本发明实施例提供的第一种情况下雨天公共空间统计量、雨天特殊子空间统计量、雨天特殊子空间统计量变化图；图6a、图6b、图6c是本发明实施例提供的第二种情况下雨天公共空间统计量、雨天特殊子空间统计量、雨天特殊子空间统计量变化图；图7a、图7b是本发明实施例提供的晴天和雨天的动态平衡关系图。
具体实施方式
15.下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于
本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
16.本发明的实施例提供了一种基于迁移学习的多模式流程工业过程的数据驱动故障检测方法，针对多模式的流程工业过程，在缺乏大量历史数据的条件下，利用迁移学习技术建立系统的故障检测模型。首先，利用tucker分解高斯核函数处理非线性数据，然后通过基于相关性信息的迁移学习方法减小源域和目标域数据分布之间的差异，获得域间共享特征。然后基于域间共享信息，利用典型多元分解技术分离公共和特殊子空间，通过主成分分析的方法建立公共子空间和特殊子空间的故障检测模型。最后，协积分分析可以揭示非平稳部分的长期的动态平稳关系，通过建立系统的动态平稳监测模型来区分模式变化和故障变化，避免系统错误地将模式变化判断为故障。
17.如图1所示，所述方法包括以下步骤：s1，采集流程工业过程的历史数据；利用基于tucker分解的高斯核函数处理非线性数据，然后基于相关性信息的迁移学习方法减小源域和目标域数据分布的差异，获得域间共享特征；s2，根据域间共享特征，基于典型多元分解和主成分分析建立流程工业过程的多模式故障检测模型；s3，根据域间共享特征，进行平稳性检验分离非平稳变量，利用协积分分析建立非平稳变量的动态平稳监测模型，最终建立一套完整的多模式流程工业过程故障检测模型；s4，利用建立好的多模式流程工业过程故障检测模型，应用于多模式流程工业过程的在线故障检测。
18.进一步地，在本发明实施例中，所述步骤s1具体包括以下步骤：s11，采集流程工业过程的历史数据；这里的流程工业过程指污水处理过程，采集的历史数据反映污水处理过程的运行状况，形成污水处理数据的数据集；采集的数据集包括作为源域的第一污水处理厂的数据和作为目标域的第二污水处理厂的数据；s12，利用步骤s11采集的数据集作为训练数据，利用基于tucker分解的高斯核函数处理非线性数据；根据tucker分解的定义，一个n阶张量x表示为如下的关于因子矩阵列向量外积的形式：其中，x是一个n阶张量，n表示张量的阶数，g是核张量，是因子矩阵，这里；表示指标集，表示核张量g在各个阶数上的维度大小，表示核张量g在各个阶数上的分量，表示各个因子矩阵的列向量；根据核函数映射理论，对已有的tucker分解式作如下的变换：
其中，表示一个核映射，表示 的高维核映射，表示 的高维核映射；假设x，y为原始空间的张量，对它们进行tucker分解：其中，x是一个n阶张量，n表示张量的阶数，表示张量x的因子矩阵的列向量；y是一个n阶张量，表示指标集，表示张量y的核张量在各个阶数上的维度大小，表示张量y的核张量在各个阶数上的分量，表示张量y的因子矩阵的列向量；在高维的特征空间中，核函数由两个高维元素的内积运算表示：其中，表示由张量x和张量y构成的核函数，表示张量x的高维核映射，表示张量y的高维核映射，表示 的高维核映射，表示 的高维核映射，表示 的高维核映射，表示 的高维核映射，表示高斯核函数；选择高斯核函数作为基础核函数，得到基于tucker分解的高斯核函数为：
其中，是高斯核函数中的控制参数，用于设置带宽，通过优化搜索算法找到最优值；s13，利用基于相关性信息的迁移学习方法减小源域和目标域数据分布的差异，获得域间共享特征；设有源域和目标域，假设源域数据是个模式的多模过程，目标域数据也是个模式的多模过程，其中，和分别表示源域数据样本和目标域数据样本的数量，表示数据样本的变量数，表示 维的实数空间，表示 维的实数空间；则有：其中，表示数据样本的变量数，表示源域第个模式的数据，表示源域第个模式数据矩阵的第个列向量，表示目标域第个模式的数据，表示目标域第个模式数据矩阵的第个列向量；在高维特征空间中，源域的每个模式的数据表示为：其中，表示一个核映射，表示 的高维映射，表示 的高维映射；源域的第个模式的协方差矩阵为：其中，表示源域第个模式的数据矩阵的行向量，表示 的高维映射；的主要特征通过寻找协方差矩阵的特征向量来求解：
其中表示点乘，表示特征值，是源域协方差矩阵的特征向量；当时，的主要特征表示为：其中，是一组系数；同理，目标域第个模式的数据的高维映射为，它的主要特征为：其中，是一组系数，表示目标域第个模式的数据矩阵的行向量，表示 的高维映射，是目标域协方差矩阵的特征向量；利用核技巧，得到：其中，表示源域的非中心核矩阵，表示源域第个模式的系数因子矩阵，源域第个模式的所有的特征值都按照从大到小的形式排列，其相应的系数因子向量为，保留前个特征值，即保留前个系数因子向量；基于相似性理论，将特征向量的比较转化为系数因子的比较，求特征向量对应的得分转化为求相应系数因子对应的得分；中心核矩阵是使用非中心核矩阵计算得到的：其中，表示全为的阶方阵，它是核矩阵中心化的辅助矩阵；因此，得到：
其中，表示源域第个模式的内核主成分矩阵的列向量，表示源域第个模式的协方差矩阵的特征向量，表示源域第个模式的系数因子矩阵的元素，表示中心核矩阵的函数，表示源域第个模式的数据，表示源域第个模式数据矩阵的行向量，表示 的高维映射，表示保留的前个特征值，即降维后的维数，；源域的第个模式的内核主成分矩阵为：其中，表示源域第个模式的内核主成分矩阵的列向量；同理，目标域的第个模式的内核主成分矩阵为：其中，表示目标域第个模式的内核主成分矩阵的列向量；源域的第个模式的系数因子矩阵表示为：同理，目标域的第个模式的系数因子矩阵表示为：其中，表示 的列向量，表示 的列向量；源域和目标域系数因子的相关性为：目标是寻求函数所有大于0.6的因子组合；然后假设其中一组为特征中心；在源域中，根据典型相关分析，源域在特征中心上的特征为：其中，表示源域在特征中心上的特征，表示源域数据与特征中心的相关性矩阵，表示 的转置，表示源域的第个模式的内核主成分矩阵；
同理，目标域在特征中心上的特征为：其中，表示目标域在特征中心上的特征，表示目标域数据与特征中心的相关性矩阵，表示目标域的第个模式的内核主成分矩阵；s14，源域数据和目标域数据之间最大平均差异距离越小，说明数据分布差异越小，因此有以下目标函数： 其中，mmd表示最大平均差异距离，表示最大平均差异距离矩阵，表示最大平均差异距离矩阵中的元素，和表示源域和目标域中内核主成分矩阵的行向量；表示源域第个模式的数据矩阵的行向量，表示源域的内核主成分矩阵的行向量，表示目标域第个模式的数据矩阵的行向量，表示目标域的内核主成分矩阵的行向量，表示矩阵的迹，，。
19.进一步地，在本发明实施例中，所述步骤s2具体包括以下步骤：s21，假设经过数据预处理的污水处理过程的数据为，它是个模式的多模过程，其中，表示样本数，表示变量数，表示 维的实数空间；则有：
其中，表示第个模式的数据，表示 的第个列向量；对于第个模式的数据来说，它构成了一个测量空间；测量空间被划分为公共子空间和特殊子空间，表示为：其中，表示模式间共享的公共子空间，表示每个模式的特殊子空间；基于以上分析，有下面这个框架：其中，表示第个模式的特征，表示第个模式的得分矩阵，表示模式内的公共特征，表示第个模式的特殊特征，表示模式内的得分矩阵，表示第个模式的特殊得分矩阵；s22，通过前面的分析，得到源域和目标域之间每个模式的共享信息为；按照张量的mode-1展开式的形式排列，被组合成一个新的三阶张量，张量沿mode-n展开成一个矩阵；张量的mode-1展开式为：其中，是样本数，是变量数，是模式数，表示 维的实数空间；假设张量构成的测量空间为，根据前面的分析，测量空间被划分为公共子空间和特殊子空间，表示为：s23，典型多元分解将一个张量分解成分量张量的和；对于一个秩为h的三阶张量，张量的典型多元分解表示为：其中，表示张量典型多元分解后的因子矩
阵，表示因子矩阵的列向量；令，典型多元分解以矩阵化的形式写成：其中，表示张量的mode-1展开式，表示张量的mode-2展开式，表示张量的mode-3展开式；利用交替最小二乘法计算出矩阵t、p、c，公共子空间被定义为：其中，，，表示因子矩阵第个模式方向的切片，表示切片的对角阵；s24，秩h由张量分解的距离差公式确定；假设经过典型多元分解之后，逆运算得到重构张量；张量分解的距离差的计算公式为：其中，f表示f范数；不同的秩h，距离差不同，当距离差最小时，此时的秩h即为所求；s25，在找出公共子空间后，直接计算每个模式的左侧部分，特殊子空间为：仿照主成分分析的方法，得到的特殊特征，所以有：其中，是的得分矩阵。
20.进一步地，在本发明实施例中，所述步骤s3具体包括以下步骤：s31，首先对源域数据进行tucker分解高斯核的非线性处理，然后利用相关性信息的迁移学习方法映射到域共享空间，得到新的域间共享特征；此时，根据建立目标域的动态平稳监测模型；选取的若干组单变量的数据，进行平稳性检验；根据先验知识和平稳性检验，分离出非平稳变量；将具有共同趋势的非平稳变量，标记为；
s32，给定非平稳时间序列，对数据做归一化处理；利用johansen多变量协整分析方法对选取的数据进行协整关系检验，通过特征值分解求解协积分矩阵的最大似然估计，最终计算协积分矩阵。
21.进一步地，在本发明实施例中，所述步骤s4具体包括以下步骤：s41，多模式非线性系统的故障检测；在线采集到的第个模式的新样本为，数据做归一化处理，然后利用tucker分解高斯核处理非线性数据，利用基于相关性信息的迁移学习方法映射到域共享空间，得到新的数据矩阵；将第个模式的新样本替换掉原来数据里的第个模式的数据，同时保持其他模式的数据不变；然后，组成一个新的张量，将这个张量沿着mode-1方向展开得到；因此，新的公共子空间的得分矩阵为：其中，p，c表示张量的典型多元分解后的因子矩阵；新的公共子空间被表示为：其中， ，，表示因子矩阵第个模式方向的切片，表示切片的对角阵；新的特殊子空间被表示为：新的特殊子空间的得分矩阵被表示为：其中，表示新的特殊特征；因此，新的特殊子空间被重新计算为：最后，剩余部分被计算为：最后，剩余部分被计算为：统计量是变量在主子空间中的投影大小，反映了每个变量的变化量，和分别用于监控公共子空间和特殊子空间的统计量，数学表达式是：
的控制限表示为：其中，表示f分布的临界值，自由度为，，置信水平为，表示样本数，表示保留的前个特征值，即降维后的维数，也是原始数据的内核主元的个数；统计量反映了数据样本在剩余子空间中的投影变化，即：统计量反映了数据样本在剩余子空间中的投影变化，即：的控制限表示为：式中，；表示数据样本协方差矩阵的第i个特征值，表示置信度下的标准正态分布的阈值；如果大于阈值，则发生的故障影响了共同特征；如果只有或大于它们的阈值，则发生的故障只影响了该模式下的特殊特征；s42，多模式非线性系统的动态平稳关系监测；在线采集到的第个模式的新样本为，数据做归一化处理，然后进行tucker分解高斯核的非线性处理，利用基于相关性信息的迁移学习方法映射到域共享空间，得到新的数据矩阵；在时刻，分离出非平稳变量，系统长期的动态平稳关系表示为：
其中e为反映了长期动态平稳关系的误差，为第个时刻的协积分矩阵；因此，监测统计量表示为：表示为：的控制限表示为：其中，和分别为的均值和方差，表示卡方分布，和是参数，置信水平为；当模式切换时，动态平稳关系被破坏，曲线波动后能恢复正常，统计量的值低于阈值；当故障发生时，动态平稳关系被破坏，曲线波动后不能恢复正常，统计量的值高于阈值。
22.下面以收集来自某污水处理过程运行数据的实例说明本发明的一种基于迁移学习的多模式流程工业过程的数据驱动故障检测方法的有效性，具体步骤包括：1）建立两个工艺参数不同的污水处理模型，采集14天污水处理过程实际运行数据和相应的生产指标，建立晴天、雨天、暴雨模式下的运行过程数据集，通过缩放、去噪对数据进行预处理。
23.2）利用基于tucker分解的高斯核函数处理非线性信息，通过基于相关性信息的迁移学习方法处理两个污水数据集，提取两个污水处理模型的域间共享特征。
24.3）根据提取的两个污水处理模型的域间共享特征，利用典型多元分解的方法分离公共子空间和特殊子空间，利用主成分分析的方法建立子空间的多模式故障检测模型。
25.4）根据提取的两个污水处理模型的域间共享特征，进行平稳性检验分离非平稳变量，利用协积分分析建立非平稳变量的动态平稳监测模型。
26.5）根据污水处理过程在线采集到的数据，实现在线故障检测，同时系统能区分模式变化和故障变化，避免系统错误地将模式变化判断为故障。
27.污水处理过程是一个复杂的非线性系统，其间要发生各种物理和生化反应，流量和负荷都会有巨大的扰动。如图2所示，污水处理模型由1个生物反应器和1个二次沉淀池组成，生物反应器包括5个混合完全的小单元。为了对该过程进行监测，一共选取了17个过程变量测量值作为数据集，采集14天污水处理过程实际运行数据。
28.污水处理厂1和污水处理厂2的过程数据采样间隔分别为4次/小时和12次/小时。污水处理厂1和污水处理厂2的模式有晴天和雨天。污水处理厂1的数据为源域，污水处理厂2的数据为目标域，故障从第7天引入。在仿真中，设定源域训练样本数目为1729。污水处理厂2的数据集用于在线检测验证。本实施例对一种基于迁移学习的多模式流程工业过程的数据驱动故障检测方法的实验结果如图3a-图3c、图4a-图4c、图5a-图5c、图6a-图6c和图7a-图7b所示。
29.如图3a-图3c所示，该实施例监测了晴天模式下的污水处理厂2的第4天到第10天的数据，当故障从第7天开始引入后，只有能检测到故障，说明该故障只影响了当前模
式的特殊特征。
30.如图4a-图4c所示，该实施例监测了晴天模式下的污水处理厂2的第4天到第10天的数据，当故障从第7天开始引入后，只有能检测到故障，说明该故障只影响了公共特征。
31.如图5a-图5c所示，该实施例监测了雨天模式下的污水处理厂2的第4天到第10天的数据，当故障从第7天开始引入后，只有能检测到故障，说明该故障只影响了当前模式的特殊特征。
32.如图6a-图6c所示，该实施例监测了雨天模式下的污水处理厂2的第4天到第10天的数据，当故障从第7天开始引入后，只有能检测到故障，说明该故障只影响了公共特征。
33.如图7a-图7b所示，该实施例监测了晴天和雨天模式下的污水处理厂2的第1天到第14天的数据，测试样本数目为4031。当统计量的值低于阈值时，表明系统的动态平稳关系不变，系统处于不同模式下的正常运行中。当故障从第7天开始引入后，第2019个样本处的统计量的值超出了阈值，系统的动态平稳关系被破坏，表明系统发生了故障。
34.综上所述，本发明在实际流程工业过程中集成了迁移学习和故障检测技术，通过基于相关性信息的迁移学习方法解决了系统建模时历史数据不足的问题，解决了目标对象无法建模的问题，能够减少目标对象建模的成本；针对多模式的流程工业过程，利用基于tucker分解的高斯核函数处理了非线性数据，解决了系统的非线性问题；通过基于典型多元分解的子空间分离的技术解决了多模式过程建模的问题，降低了建模成本，提高了系统的检测效率；在故障检测的过程中，系统可以自主判断当前的扭曲变化属于模式变化还是故障变化；通过协积分分析技术建立系统的动态平稳监测模型，来区分模式变化和故障变化，避免系统错误地将模式变化判断为故障，提高了系统检测的准确率。
35.需要说明的是，在本文中，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者终端设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者终端设备所固有的要素。在没有更多限制的情况下，由语句“包括一个
……”
限定的要素，并不排除在包括所述要素的过程、方法、物品或者终端设备中还存在另外的相同要素。
36.在说明书中提到“一个实施例”、“实施例”、“示例性实施例”、“一些实施例”等指示所述的实施例可以包括特定特征、结构或特性，但未必每个实施例都包括该特定特征、结构或特性。另外，在结合实施例描述特定特征、结构或特性时，结合其它实施例（无论是否明确描述）实现这种特征、结构或特性应在相关领域技术人员的知识范围内。
37.本发明涵盖任何在本发明的精髓和范围上做的替代、修改、等效方法以及方案。为了使公众对本发明有彻底的了解，在以下本发明优选实施例中详细说明了具体的细节，而对本领域技术人员来说没有这些细节的描述也可以完全理解本发明。另外，为了避免对本发明的实质造成不必要的混淆，并没有详细说明众所周知的方法、过程、流程、元件和电路等。
38.本领域普通技术人员可以理解实现上述实施例方法中的全部或部分步骤是可以通过程序来指令相关的硬件来完成，该程序可以存储于计算机可读取存储介质中，如：rom/ram、磁碟、光盘等。
39.以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。