基于低碳排放的高密城区铁路线路精细优化方法

本发明涉及铁路线路精细优化，具体地说，涉及一种基于低碳排放的高密城区铁路线路精细优化方法。

背景技术：

1、随着大都市社会经济的快速发展，世界范围内的城市化进程也在快速推进。再加上大规模的城市和城际快速交通建设带来的交通便利性和流动性的提高，使得跨区域的城际铁路出行成为可能，并呈现出不断发展的趋势。城市地区的铁路设计与其他地区的铁路设计不同，因为城市地区有明显的特点，如土地成本高、建筑拆迁成本高，以及由此带来的碳排放增加。尽管在人工走线设计中已经考虑了许多控制因素，但要实现最佳设计是很困难的。

2、在高密度城市地区的铁路线路设计会遇到以下困难和挑战。1)虽然这些住区的建筑可能不高(1-3层)，或者面积不大，但分布非常密集；2)如果不仔细合理地设计线路，铁路建设工程可能会产生巨大的房屋拆迁补偿费用；3)由此产生的房屋拆迁和新建的碳排放会进一步恶化当地的生态环境。

3、铁路选线设计是一个复杂的优化过程，综合了政治、经济、文化、生态、地质等问题。目前的铁路选线设计方法一般是以人工设计为主。先选择一个可行的、合理的走廊，解决政治和文化问题，同时考虑到经济、生态和地质等方面。在选择走廊后，初步走线设计致力于确定垂直和水平方面的详细走线参数，同时考虑到走线的成本、地形、地质和生态。在这个阶段，设计开始进入细化设计模式。值得注意的是，我们提出的微调算法是在初步人工设计完成后的初步设计阶段应用的。给定一个人工确定的路线，本研究根据线形特点进行精细化优化。

4、由于人力的限制，要列举所有可能的走线几乎是不可能的。此外，在高密度的住宅区，水平线的轻微偏差都会对建筑物的拆除造成很大影响。为了解决这个问题，人们可以利用计算机提供的高计算能力，在初步设计阶段对现有的人工定线进行进一步的微调。因此，人类经验和计算机算法的优势可以得到合理的整合。基于工程成本、碳排放和土地使用的节约，可以进一步提高线形设计的效率。

5、目前，关于铁路线路的精细优化设计的研究很少。此外，关于建筑拆迁节约和碳排放的研究也很少。dp(动态规划)在线形优化领域的应用已经有较长的时间，但它是在交点数量固定的预可行性和可行性研究阶段使用的。由于交叉点太多，搜索范围有限，最近它的应用已经大大减少。

6、有人用dp方法进行了三维铁路线形优化，在固定的水平交叉点数量和间距的情况下，找到了最佳的走廊线形，然后用改进的方向来完善走廊。用dp方法进行了三维铁路线形优化，在水平交叉点数量和间距固定的情况下，找到了最佳的走廊线形，然后用改进的方向加速法对走廊进行了完善。一些研究者提出，对于预先选定的平面线型，在有一定数量的纵断面变坡点的情况下，使用dp程序进行纵断面线型的优化。

7、然而，用dp算法进行优化时，交点的数量和位置是事先给定的，在优化过程中不能调整交点的数量。因此，dp算法在寻找最优走廊的过程中很难达到理想的效果。

技术实现思路

1、本发明的内容是提供一种基于低碳排放的高密城区铁路线路精细优化(fora)方法，其能够克服现有技术的某种或某些缺陷。

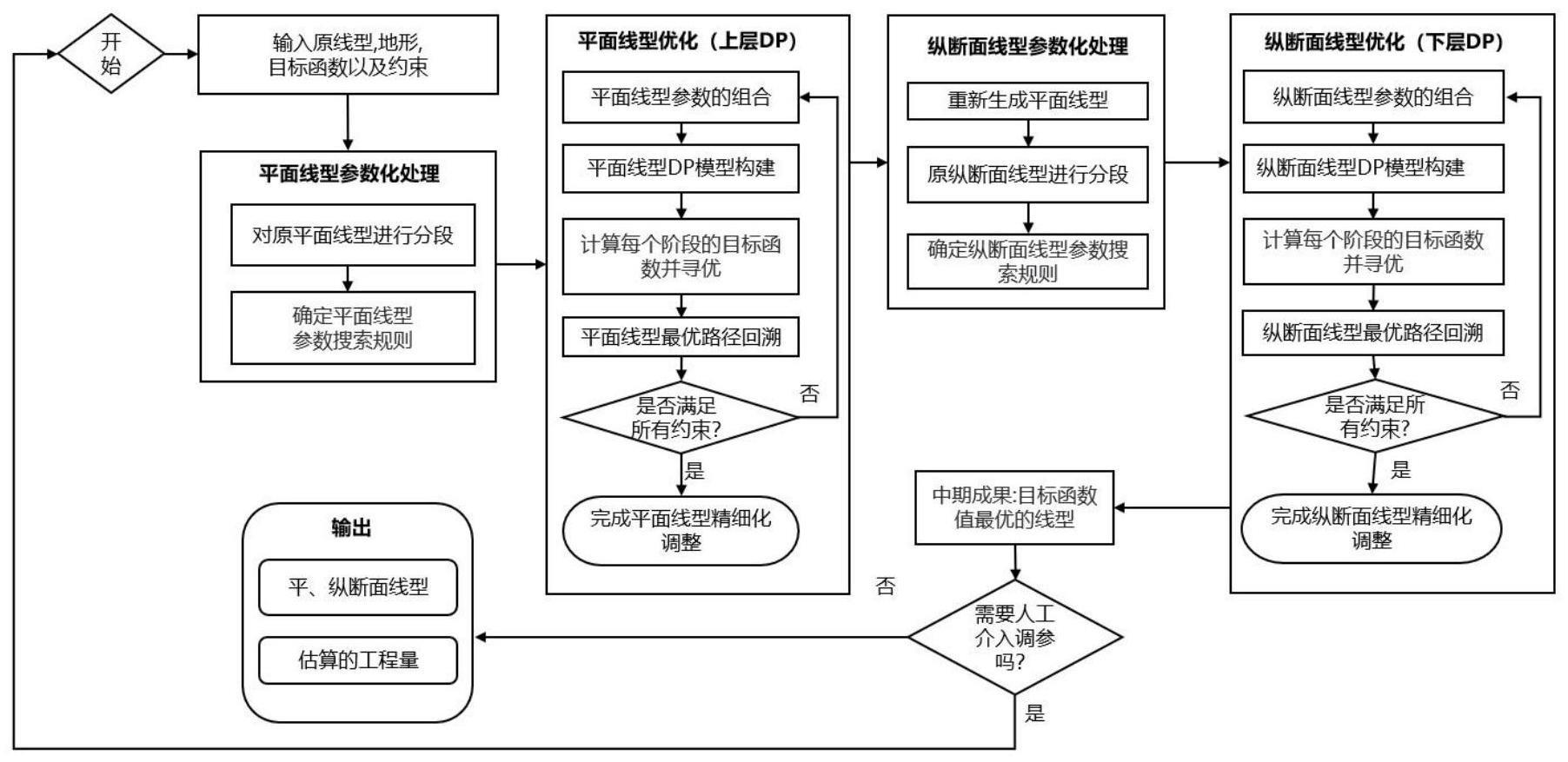
2、根据本发明的一种基于低碳排放的高密城区铁路线路精细优化方法，其包括以下步骤：

3、步骤1、输入原始数据，包括铁路线型、地形、目标函数以及约束；

4、步骤2、平面线型参数化处理；

5、步骤2.1、对原平面线型进行分段；

6、步骤2.2、确定平面线型参数搜索规则；

7、步骤3、平面线型优化；

8、步骤4、纵断面线型参数化处理；

9、步骤4.1、重新生成平面线型：将步骤3生成的平面线型作为纵断面优化的输入平面线型；

10、步骤4.2、对原纵断面线型进行分段；

11、步骤4.3、确定纵断面线型参数搜索规则；

12、步骤5、纵断面线型优化；

13、步骤6、得到目标函数值最优的线型，检查线型是否符合要求；若符合，直接输出优化后的平、纵断面线型及估算的工程量；若不符合，则重复步骤1-5。

14、作为优选，铁路线型是一条分布在三维空间的曲线，这条曲线在水平面上的投影称为平面线型ha；在这条曲线上，以ha的长度为标点，以标高为序点的平面上的投影，称为纵断面线型va；一个ha单元是一系列直线段、圆曲线和缓和曲线的组合；铁路ha单元由切线-缓和曲线-圆曲线-缓和曲线-切线组成；

15、ha是水平交点hpi坐标的一个函数(x,y)的函数，如公式(1)所示，起点和终点hpi的坐标被表示为(x0,y0)和(xn+1,yn+1)；

16、

17、其中i＝1,2,…,n+1表示第i个hpi；xi,yi,rhi,lsi是ha函数的四个变量；rh为圆曲线的半径，ls为缓和曲线的长度；

18、同样，va是一系列直线段和圆曲线的组合，va的基本单位由切线-圆曲线-切线组成；与ha不同，va上每个点的位置由里程k和设计高程e表示；va是vpi位置和圆曲线半径的一个函数rv，如公式(2)所示，起点和终点的vpi位置分别表示为(k0,e0)和(km+1,em+1)；

19、

20、其中j＝1,2,…,m+1表示第j个vpi；kj,ej,pvj是va函数的三个变量；

21、这些变量组(xi,yi,rhi,lsi,kj,ej,rvj)是对准参数的基本构成部分；空间中的三维线型可以由这些参数描述。

22、作为优选，影响平面线型的约束条件如下：

23、(1)ha中一条圆曲线的半径rh应超过最小允许半径rhcmin，并表示如下：

24、rh-rhcmin≥0                          (3)

25、(2)水平排列中的一条缓和曲线ls的长度应超过最小允许缓和曲线lscmin，并表示如下：

26、ls-lscmin≥0                    (4)

27、(3)一个圆形曲线的长度lhc在水平方向上应超过最小允许曲线长度lhcmin，并表示如下：

28、lhc-lhcmin≥0                     (5)

29、(4)两个相邻的水平曲线之间的切线长度lt至少应是最小允许切线长度ltmin，具体如下：

30、

31、ltmin-lt≤0                     (7)。

32、作为优选，影响纵断面线型的约束条件如下：

33、1)在纵断面上的纵坡gi应小于允许的最大纵坡gmax，表示如下：

34、gi≤gmax                    (8)

35、2)va中一条竖曲线的半径rv应超过最小允许竖曲线半径rvcmin，并表示如下：

36、rv-rvcmin≥0                    (9)

37、3)坡长应不低于最小允许坡长lsmin，具体如下：

38、

39、4)凸、凹竖曲线的长度应不小于凸形竖曲线允许最小长度lvcmin，凹形竖曲线允许最小长度lvsmin具体如下：

40、lvc≥lvcmin                      (11)

41、lvs≥lvsmin                      (12)。

42、作为优选，目标函数被定义为总的建筑成本cc，包括以下部分：土方工程费用ce，桥梁费用cb，隧道费用ct，与长度有关的费用cl，征地费用cr，建筑物拆除费用cbd，建筑物的二氧化碳排放惩罚成本ccb，以及铁路基础设施ccr；

43、cc＝ce+cb+ct+cl+cr+cbd+ccb+ccr                (13)

44、(a)土方工程费ce

45、

46、ω0,ω1,ω2＝0 or 1；ω0+ω1+ω2＝1

47、式中，ω0＝1为全挖方断面；ω1＝1为全填方断面；ω2＝1为半填半挖断面；aci和afi分别为第i个横断面挖方和填方的面积；uf、uc分别为填、挖方单价；lei为第i个横断面的长度；

48、(b)桥梁费用cb

49、

50、式中，n为全线桥梁的数量；ubi为第i座桥梁的单位建造成本；li为第i座桥梁的长度；cai第i座桥梁桥台的建造费用；

51、(c)隧道费用ct

52、

53、式中，n为全线隧道的数量；uti为第i座隧道的单位建造成本；li为第i座隧道的长度；cpi第i座隧道洞口的建造费用；

54、(d)与长度有关的费用cl

55、cl＝ul×l；

56、式中，ul为线型费用的单位建造成本；l为线路总长；

57、(e)征地费用cr

58、

59、式中，uri为线路穿越不同区域时的单位征地费用；ari为线路穿越区域所占用的面积；

60、(f)建筑物拆除费用cbd

61、cbd＝∑iai×uh                     (14)

62、其中uh是一个建筑物的单位成本，ai为第一栋楼的建筑面积i的建筑面积；

63、(g)建筑物的二氧化碳排放惩罚费用ccb

64、ccb＝(cjc+cjz+ccc)×a×fc               (15)

65、其中cjc是建筑材料生产和运输过程中单位建筑面积的碳排放量；cjz为建筑施工阶段每单位建筑面积的碳排放量；ccc为建筑拆除阶段单位建筑面积的碳排放量；a是建筑面积；以及fc是在洲际交易所查询到的碳排放交易价格；

66、(h)铁路基础设施的二氧化碳排放处罚费用

67、铁路基础设施的二氧化碳排放惩罚成本ccr定义如下：

68、ccr＝(cer+cmr)×fc                  (21)

69、其中cer是铁路建设阶段的碳排放量；cmr是铁路材料生产和运输阶段的碳排放；fc是在洲际交易所查询到的碳排放交易价格；

70、基础设施建设期间的能源消耗和总碳排放量按公式(22)和(23)计算如下：

71、

72、

73、其中fci表示第i种设备的燃料消耗；mcr,i是指第i种铁路建筑材料的消耗量；和dcr,i是第i种铁路建筑材料的平均运输距离。

74、作为优选，平面、纵切面线型参数搜索规则如下：在平面线型中，hpi坐标的变化被认为是在参考点附近以一定的步长进行枚举；rh的变化基于原始值的rh并以100米为步长进行枚举；ls也用同样的方法列举，步长为10米；最后，对列举的参数进行排列组合，用计算机对每个方案进行试算，从而得到最优值；

75、va中变量的列举和组合与ha中的类似，但是，k应该是50米的整数倍，而rv应该是1000米的整数倍。

76、作为优选，平面线型优化的优化方法，即上层dp方法为：

77、阶段划分

78、引入用于分阶段划分的辅助点，称为可移动点mp，mp的数量为k-2；用基本的ha单位来划分排列，所以有k＝0,1,…,n-1 dp stages，这种排列组合的阶段呈现如下:stage＝0,hpi0to mp2；stage＝1,mp1to mp2；stage＝k,mpk to mpk+1；...；stage＝n-2,mpn-2tompn-1；stage＝n-1,mpn-1to hpin+1；

79、状态

80、与优化问题的每个阶段相关联的是过程的状态，这些状态反映了全面评估当前决策对未来行动的影响所需的信息，状态变量是参数的列举值，状态空间s被划分为k集s＝{s0,…,sk,…,sn-1}；

81、阶段的参数枚举值表示为k阶段的参数枚举值表示如下：

82、

83、

84、

85、其中i＝0,1,…,r，和r代表hpi坐标的枚举数量；ir＝0,1,…,kr,kr代表参数的枚举数rh的枚举数；和il＝0,1,…,kl,kl代表参数的枚举数ls；

86、决策变量

87、ha基本单元的计算表示为：

88、hak＝f(xk-1,yk-1,xk,yk,xk+1,yk+1,rhk,lsk)           (26)

89、决策是指在一个阶段选择所有备选方案的最佳设计序列，阶段中的状态变量的值k+1的值不仅取决于阶段的状态变量的值k阶段的状态变量的值，而且还取决于k-1阶段的状态变量的值；

90、因此，如果决策变量的值uk(sk-1,sk)的值被确定，状态变量的值sk+1在第k+1阶段的状态变量的值也完全确定，也就是说：

91、

92、决策变量被说明如下：

93、

94、状态转移

95、状态转移函数用于描述相邻阶段之间的参数过渡，这个转移函数从k阶段到k+1阶段的过渡函数说明如下：

96、

97、状态和状态转换拥有以下属性：

98、属性1、模型的下一个状态只与当前阶段有关；

99、属性2、状态转换只发生在两个相邻的阶段之间；

100、属性3、不同的hpi连接序列可达到状态空间中的相同状态；

101、属性4、阶段中的状态变量的值k+1阶段的状态变量的值不仅取决于阶段的状态变量的值k阶段的状态变量的值，而且还取决于阶段的状态变量的最佳值；

102、决策

103、决策序列包括从第0或第k阶段的开始到结束的过程；k阶段开始到第n+1组成的决策序列被称为整个过程的政策，即：

104、p0n(s0)＝{u0(s0),u1(s1),…,un(sn)}          (30)

105、pkn(sk)＝{uk(sk),uk+1(sk+1),…,un(sn)}             (31)

106、满足约束条件的所有政策的集合被称为允许政策的集合，用p表示，如下所示：

107、p0n(s0)∈p0n(s0)or pkn(sk)∈pkn(sk)              (32)

108、准则函数

109、对于有多个预设的状态，准则函数被用来指导决策和找到最佳预设；

110、根据公式(1)，(2)和(12)，建筑成本取决于ha和va，可以表示为：

111、cc(f(.),g(.))＝cc(f(xi,yi,rhi,lsi)),g(kj,ej,rvj))          (33)

112、其中g(.)代表纵断面线型函数，基准线的纵断面线型参数用于第一次迭代计算；

113、状态k阶段sk(hpik,rhk,lsk)至k+1阶段sk+1(hpik+1,rhk+1,lsk+1)阶段的的建筑成本表示如下：

114、

115、过程函数如下：

116、

117、

118、最佳目标函数值如下：

119、

120、递归方程表示如下：

121、

122、边界条件如下：

123、fn+1(sn+1)＝0                   (39)

124、递归方程可推导出k＝n，然后就实现最优决策和最佳目标函数；当k＝0,f0(s0)可获得，这也是整个优化问题的解；

125、用cck来表示从状态s0(hpi0,rh0,ls0)到状态sk(hpik,rhk,lsk)；定义状态的评判函数为sk(hpik,rhk,lsk)的标准函数如下：

126、

127、其中pk-1记录了从前任状态中的sk-1到状态sk(hpik,rhk,lsk)。

128、作为优选，纵断面线型的优化方法，即下层dp方法为：

129、阶段划分

130、以基本的va单位来划分排列，所以有k＝0,1,…,m-2dp阶段；

131、状态

132、以sk(vpik,rvk)作为一个状态，sk(vpik,rvk)∈sk.的参数枚举值可以表示为：

133、

134、其中j＝0,1,…,v,v代表vpi坐标的枚举数量；jv＝0,1,…,kv,kv代表参数的枚举数rv；

135、决策变量

136、决策变量表示当第i个阶段进入到第i+1个阶段时做出的决定；允许的决策集如下：

137、

138、状态转移

139、状态转移说明如下：

140、

141、决策

142、决策流程如下：

143、

144、准则函数

145、状态k阶段sk(vpik+1,rvk+1)至k+1阶段sk+1(vpik+1,rvk+1)阶段的建筑成本表示如下：

146、

147、过程函数如下：

148、

149、用cck来表示从状态s0(vpi0,pv0)到状态sk(vpik,rvk)，定义状态的标准函数为sk(vpik,rvk)的标准函数如下：

150、

151、其中pk-1记录了从先前的状态在sk-1到状态sk(vpik,rvk)。

152、本发明提出了一个新的模型，称为铁路线路精细优化(fora)，用于精细优化铁路线路设计。本发明将fora模型应用于人工选择走廊后的初步设计阶段，有效地结合了人类经验和计算机算法的优势。

153、本发明根据铁路线形的特点，开发了一种双层动态规划(dp)算法，这是fora的核心。上层是调整平面线型，而下层是调整纵断面线型。这个框架可以同时获得更好的解决方案并降低计算的复杂性。

154、作为一个重要的指标，二氧化碳的排放也参与了线形优化计算。