基于任意高阶时域有限差分方法的局部时间步进方法

1.本发明属于时域有限差分方法数值计算技术，具体是一种基于任意高阶时域有限差分方法的局部时间步进方法。


背景技术：

2.多尺度问题出现在众多实际电子工程领域中，如复杂系统电磁干扰、电磁兼容及通信信道分析等。由于精细结构的存在，传统的时域有限差分方法需采用小尺寸剖分网格模拟物理模型，同时受稳定性条件的限制，时间迭代步长选取过小，导致系统仿真耗时严重。


技术实现要素：

3.本发明的目的在于提供一种基于任意高阶时域有限差分方法的局部时间步进技术。
4.实现本发明目的的技术方案为：一种基于任意高阶时域有限差分方法的局部时间步进方法，步骤如下：
5.步骤1，建立目标的几何模型，使用非均匀yee网格对模型进行离散；
6.步骤2，用麦克斯韦方程组描述yee网格上的电场和磁场的关系，在麦克斯韦方程中，电磁场对空间的偏微分采用中心差分进行代替，电磁场对时间的偏微分按照高阶的泰勒公式进行展开；
7.步骤3，计算各个yee网格单元满足稳定性条件的不同时间步长，从小到大依次排列为δti,i＝1,2,
…
,n,n为不同时间步长个数，其中δt
i+1
＝niδti，ni为自然数，令时间步长δti对应yee网格为细网格，时间步长δt
i+1
对应yee网格为粗网格，起始时，i＝1；
8.步骤4，对细网格中的电磁场进行迭代求解，细网格的电磁场迭代ni个时间步后，时间步长δt
i+1
对应yee网格的电磁场开始迭代，如果迭代过程中细网格迭代相邻位置没有粗网格，细网格电磁场按泰勒公式展开进行迭代；如果细网格迭代过程中用到粗网格的电磁场，由已知的粗网格电磁场信息通过泰勒公式插值得到；
9.步骤5，当粗网格的电磁场迭代完一个时间步长δt
i+1
，返回步骤4，直到细网格的电磁场迭代了nin
i+1
个时间步长，粗网格的电磁场迭代了n
i+1
个时间步长，令i＝i+1，将下一时间步长δt
i+1
对应yee网格作为粗网格，之前的粗网格变成细网格，返回步骤4，进行粗细网格上的电磁场迭代求解，直到所有网格的电磁场都迭代完，得到空间中任意时刻的电磁场值信息。
10.优选地，在yee网格单元中，电磁场满足无源微分形式的麦克斯韦旋度方程，具体为：
11.[0012][0013]
式中ε、μ分别表示介电常数和磁导率，e和h分别表示电场强度和磁场强度；
[0014]
将麦克斯韦旋度方程的旋度进行展开，整理并简化，得
[0015][0016]
其中e
x
，ey和ez分别为电场在直角坐标系下x，y和z的三个分量，h
x
，hy和hz分别为磁场在直角坐标系下x，y和z的三个分量；
[0017]
磁场z分量对空间的偏微分为对在直角坐标系中空间位置处采用中心差分进行展开：
[0018][0019]
公式(3)中q第一行乘以u第一项展开为：
[0020][0021]
同时，电磁场关于空间的偏微分用中心差分展开；
[0022]
根据m阶泰勒公式展开，求得下一时刻的电场和磁场值：
[0023][0024]
其中t表示时间刻，δt表示迭代采用的时间步长，根据公式(3)，将公式(5)中电磁场对时间的高次导变为对空间的多次导，得到任意高阶(m阶)时域有限差分方法的迭代公式：
[0025][0026]
优选地，计算各个yee网格单元满足稳定性条件的不同时间步长的具体方法为：
[0027]
yee网格单元的δt选取，满足稳定性条件，考虑时谐场情况，即
[0028]
f(x,y,z,t)＝f0(x,y,z)e
jωt
ꢀꢀ
(7)
[0029]
其中ω代表角频率，f0(x,y,z)表示坐标(x,y,z)场值，公式(7)是下面一阶微分方程的解：
[0030][0031]
公式(5)按公式(8)进行整理化简，变为：
[0032][0033]
对公式(9)化简整理，得：
[0034][0035]
其中q表示数值增长因子，数值稳定性要求在时间t趋于无穷，δt足够小时，增长因子需要满足|q|≤1，令a＝ωδt，满足|q|≤1解的集合为：
[0036][0037]
从麦克斯韦方程可导出电磁场任意直角分量均满足齐次波动方程：
[0038][0039]
其中c代表光在媒质中的传播速度，考虑平面波的解，即：
[0040][0041]
其中f1为常数，采用中心差分近似，公式(12)中的二阶导数近似为：
[0042][0043]
其中δx、δy和δz分别代表yee网格单元在x、y和z轴上的长度，将公式(13)代入到公式(14)得：
[0044][0045]
波动方程的离散式为：
[0046][0047]
离散后平面波式(13)中波矢量与频率之间应该满足的关系式，上式改写为：
[0048][0049]
上式对于任意的k
x
，ky，kz均成立的充分条件是
[0050][0051]
满足稳定性条件的最大δt为yee网格单元的时间步长。
[0052]
优选地，细网格中电磁场采用m(m≥1)阶泰勒公式展开：
[0053][0054]
其中uf为细网格中的电场和磁场，δtf为细网格中电磁场迭代的时间步长，n为正整数，1≤n≤n；
[0055]
(a)、跟粗网格不相邻的细网格电磁场进行迭代时，上式变换为：
[0056][0057]
当细网格中电磁场迭代时，需要用到相邻粗网格中的电磁场信息，上式右边第二项进行展开：
[0058][0059]
上式中右边第一项是细网格场值正常更新部分，第二项是粗细网格相邻处需要传值或插值的部分，将表示成泰勒公式展开的形式，利用粗网格上一时刻的电磁场信息进行求解：
[0060][0061]
由此，得到细网格在粗细网格相邻处的电磁场迭代公式：
[0062][0063]
当迭代到t+niδtf时刻，表示已完成单时间步内的细网格场值迭代；
[0064]
(b)、粗网格的场值迭代：
[0065][0066]
粗网格场值迭代到粗细相邻处时，需要用到的细网格场值信息，该信息已经在细网格电磁场迭代中求得，直接使用进行迭代
[0067]
本发明与现有技术相比，其显著优点：(1)本发明可以实现不同时间步长的非均匀
yee网格电场和磁场的迭代，减少计算所需的时间。(2)本发明可以获得比传统时域差分方法更高的精度。
附图说明
[0068]
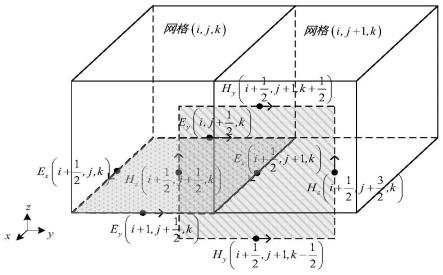
图1是yee网格。
[0069]
图2是计算区域不同时间步长迭代示意图。
[0070]
图3是金属目标模型示意图。
[0071]
图4是观察点时域波形比较图。
具体实施方式
[0072]
下面结合附图对本发明作进一步详细描述。
[0073]
本发明是一种基于任意高阶时域有限差分方法的局部时间步进技术，步骤如下：
[0074]
步骤1，建立目标的几何模型，使用非均匀yee网格对模型进行离散。
[0075]
步骤2，用麦克斯韦方程组描述yee网格上的电场和磁场的关系，在麦克斯韦方程中，电磁场对空间的偏微分采用中心差分进行代替，电磁场对时间的偏微分按照高阶的泰勒公式进行展开。
[0076]
已知无源微分形式的麦克斯韦旋度方程：
[0077][0078][0079]
式中ε、μ分别表示介电常数和磁导率，e和h分别表示电场强度和磁场强度；
[0080]
将麦克斯韦旋度方程的旋度进行展开，整理并简化，得
[0081][0082]
其中e
x
，ey和ez分别为电场在直角坐标系下x，y和z的三个分量，h
x
，hy和hz分别为磁场在直角坐标系下x，y和z的三个分量；
[0083]
磁场z分量对空间的偏微分为对在直角坐标系中空间位置
处采用中心差分进行展开：
[0084][0085]
公式(3)中q第一行乘以u第一项展开为：
[0086][0087]
同时，电磁场关于空间的偏微分用中心差分展开；
[0088]
根据m阶泰勒公式展开，求得下一时刻的电场和磁场值：
[0089][0090]
其中t表示时间刻，δt表示迭代采用的时间步长，根据公式(3)，将公式(5)中电磁场对时间的高次导变为对空间的多次导，得到任意高阶(m阶)时域有限差分方法的迭代公式：
[0091][0092]
步骤3，计算出各个yee网格单元满足稳定性条件的不同时间步长，从小到大依次排列为δti,i＝1,2,
…
,n,n为不同时间步长个数，其中δt
i+1
＝niδti，ni为自然数，令时间步长δti对应yee网格为细网格，时间步长δt
i+1
对应yee网格为粗网格，起始时，i＝1；
[0093]
yee网格单元的δt选取，满足稳定性条件，考虑时谐场情况，即
[0094]
f(x,y,z,t)＝f0(x,y,z)e
jωt
ꢀꢀ
(7)
[0095]
其中ω代表角频率，f0(x,y,z)表示坐标(x,y,z)位置的场值，公式(7)是下面一阶微分方程的解：
[0096][0097]
公式(5)按公式(8)进行整理化简，变为：
[0098][0099]
对公式(9)化简整理，得：
[0100][0101]
其中q表示数值增长因子，数值稳定性要求在时间t趋于无穷，δt足够小时，增长因子需要满足|q|≤1，令a＝ωδt，满足|q|≤1解的集合为：
[0102]
[0103]
从麦克斯韦方程可导出电磁场任意直角分量均满足齐次波动方程：
[0104][0105]
其中c代表光在媒质中的传播速度，考虑平面波的解，即：
[0106][0107]
其中f1为常数。采用中心差分近似，公式(12)中的二阶导数近似为：
[0108][0109]
其中δx、δy和δz分别代表yee网格单元在x、y和z轴上的长度，将公式(13)代入到公式(14)得：
[0110][0111]
公式(12)中其余两项二阶导数的差分近似也有类似形式，因此波动方程的离散式为
[0112][0113]
离散后平面波式(13)中波矢量与频率之间应该满足的关系式，上式可改写为：
[0114][0115]
上式对于任意的k
x
，ky，kz均成立的充分条件是
[0116][0117]
满足稳定性条件的最大δt为yee网格单元的时间步长。
[0118]
步骤4，对细网格中的电磁场进行迭代求解，细网格的电磁场迭代ni个时间步后，时间步长δt
i+1
对应yee网格的电磁场开始迭代，每个网格上的电磁场迭代会用到相邻网格上电磁场。由位置信息可以判断，如果迭代过程中细网格迭代相邻位置没有粗网格，那么细网格电磁场按泰勒公式展开进行迭代。如果细网格迭代过程中用到粗网格的电磁场，可由前一时刻的粗网格电磁场信息通过泰勒公式插值得到；
[0119]
细网格中电磁场采用m阶泰勒公式展开：
[0120][0121]
其中uf为细网格中的电场和磁场，n为正整数，1≤n≤n。
[0122]
当网格(i,j+1,k)是粗网格，网格(i,j,k)是细网格，网格(i,j+1,k)上电磁场迭代之前，需要知道周围的四个磁场(如图1蓝色框所示)，所在网格的δt与网格(i,j+1,k)不同，这时需要通过插值计算出操作如(a)所示。当网格(i,j+1,k)和网格(i,j,k)是细网格，操作如(b)所示。
[0123]
(a)、跟粗网格不相邻的细网格电磁场进行迭代时，公式(19)可以变换：
[0124][0125]
当细网格中电磁场迭代时，需要用到相邻粗网格中的电磁场信息。公式(19)右边第二项按公式(3)进行展开：
[0126][0127]
上式中右边第一项是细网格场值正常更新部分，第二项是粗细网格相邻处需要传值或插值的部分，由于为未知量，可以将该项表示成泰勒公式展开的形式，利用粗网格上一时刻的电磁场信息进行求解：
[0128][0129]
由此，可以得到细网格在粗细网格相邻处的电磁场迭代公式：
[0130][0131]
当迭代到t+niδtf时刻，表示已完成单时间步(δtc)内的细网格场值迭代。
[0132]
(b)、粗网格(时间步长为δtc)的场值迭代：
[0133][0134]
粗网格场值迭代到粗细相邻处时，需要用到的细网格场值信息，该信息已经在细网格电磁场迭代中求得，可直接使用进行迭代。
[0135]
步骤5，上述为一级局部时间步进步骤，当细网格的电磁场迭代了nin
i+1
个时间步，粗网格的电磁场迭代了n
i+1
个时间步，令i＝i+1，将下一时间步长δt
i+1
对应yee网格作为粗网格，之前的粗网格变成了细网格。以次类推循环，可以完成所有非均匀yee网格中的场值迭代，直至所有场值迭代的总时刻满足需求。
[0136]
数据后处理，根据计算出的场值提取相关的物理参数。
[0137]
为了验证本发明的正确性与有效性，下面分析了一个金属模型的电磁散射特性。算例：计算模型如图2所示，cfdtd计算区域网格数64*204*850，总场边界区域，在x方向上设置在第23和第42网格，在y方向上设置在第23和182网格，在z方向上设置在第235和第635网格，入射角度θ＝90
°
，入射脉冲中心频率150ghz,脉宽2.4ns，δx＝δy＝10
·
δz＝
0.0002m，迭代时间步数6000步，观察点所在网格(17，17，285)，cfdtd计算区域中，x和y方向上pml到外推网格数都是6，外推到总场网格数都是6，总场到散射体的距离网格数都是5，pml层数是10层。而在z方向上pml到外推网格数都是60，外推到总场网格数都是60，总场到散射体的距离网格数都是50，pml层数是100层。cfdtd耗时21484s。基于任意高阶时域有限差分方法的局部时间步进技术(lts-ader-fdtd)计算区域网格64*204*94，在x方向上设置在第23和第42网格，在y方向上设置在第23和182网格，在z方向上设置在第23和第72网格，z方向上第33行网格到37行网格和第58行网格到第62行网格都是细网格，尺寸为δx＝δy＝10
·
δz＝0.0002m，其他行网格都是粗网格，尺寸为δx＝δy＝δz＝0.0002m，粗网格迭代时间步数1000步，观察点所在网格(17，17，28)，lts耗时2281s。
[0138]
表1各算法耗时对比图
[0139]
算法耗时cfdtd(均匀网格)21484sader-fdtd(非均匀网格)7264slts-ader-fdtd(非均匀网格)2281s