一种基于APSO-HMM的滑坡时间预测方法

本发明属于地质灾害监测，具体一种基于apso-hmm的滑坡时间预测方法。

背景技术：

1、我国地质和地理环境复杂，气候条件时空差异大，地质灾害种类多、分布广、危害大，滑坡产生的安全隐患也不断受到重视。在滑坡等地质灾害预警监测中，目前普遍以群测群防为主，然而通过群测群防方法所获数据并不精细，通常仅是定性判断；此外在监测内容记录和上报方面多采用纸笔记录，缺乏信息反馈机制，无法做到快速上报，且监测数据分析方面缺少直观、科学、快速的分析手段，还需消耗大量人力。而传统的专业监测是由政府或企业投入经费，委托专业机构，利用监测仪器设备获取高精度监测数据，再进行内业整理，从数据获取到分析完毕耗时较长，使得监测结果难以及时反映地质灾害的状态。此外传统的变形监测又不能实时反馈监测目标的整体状态，使得人身安全和设备安全得不到有效保障，难以保障滑坡监测的有效性。

2、基于北斗微动装置的监测数据在滑坡地质灾害监测中起到关键性参考作用，本专利基于gmm方法重构北斗微动装置采集的位移数据，针对hmm模型参数学习算法易收敛于局部极值的问题，提出一种引入扰动因子的自适应粒子群算法aspo，并将该方法应用于隐马尔科夫模型的训练，实现对隐马尔科夫模型初始参数的优化。进而改进hmm模型应用于地质灾害滑坡预警中，实现对滑坡地质灾害实时化、精准化的预警监测。

技术实现思路

1、本发明的目的是提供一种基于apso-hmm的滑坡时间预测方法，用于解决现有技术从数据获取到分析完毕耗时较长，监测结果难以及时反映地质灾害的状态，监测实时化、精准化较差不能满足要求的技术问题。

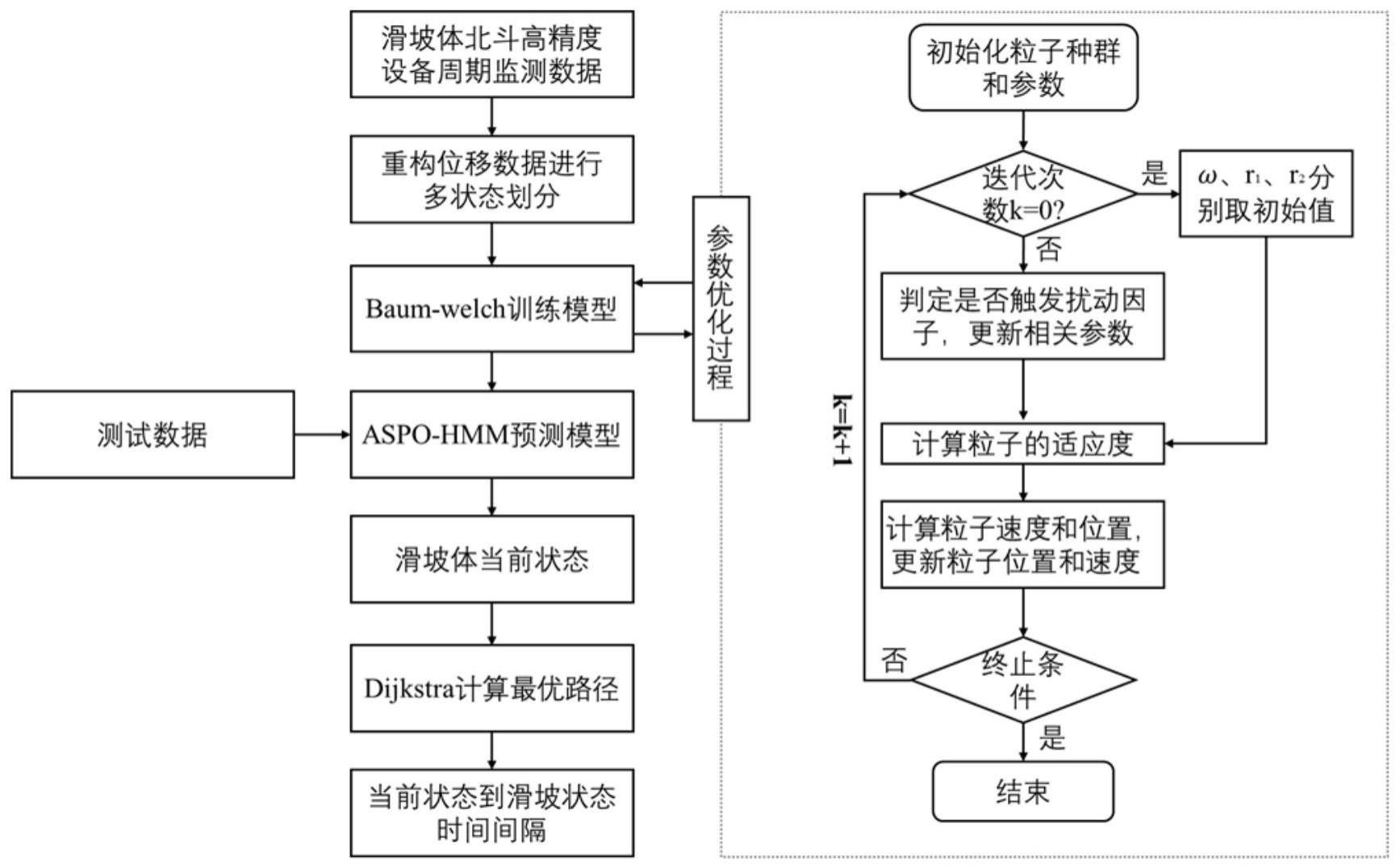
2、所述的一种基于apso-hmm的滑坡时间预测方法，包括下列步骤：

3、步骤1、采集的滑坡全周期位移数据进行预处理，并对采集的位移数据在时序方向上进行多状态划分。

4、步骤2、对以上划分过状态的滑坡位移数据用baum-welch算法进行训练，采用带扰动因子的自适应粒子群优化隐马尔可夫模型参数，训练并构造滑坡演化状态模型apso-hmm。

5、步骤3、滑坡演化状态模型利用viterbi算法对实时采集数据进行状态解码得到时间序列对应状态序列，并将当前估计状态作为dijkstra算法的输入，从而预判出滑坡可能发生的时间。

6、优选的，所述步骤1包括：

7、步骤1.1：通过北斗监测装置获取滑坡位移原始数据进行预处理，根据监测点每天观测数据(x，y，z)计算出的l，即合位移速率，数据时序化形成观测序列d；

8、步骤1.2：基于混合高斯方法重构滑坡位移数据，进行多状态位移划分，并设置滑坡安全阈值l0，状态数n，每个状态中的高斯混合数m。

9、优选的，所述步骤1.1中，根据监测点每天观测数据(x，y，z)计算合位移速率l，公式具体如下：

10、

11、其中，t为当前时刻，t-1为上一时刻，(xt，yt，zt)表示当前时刻t的观测数据，(xt-1，yt-1，zt-1)表示当前时刻t-1的观测数据；

12、所述步骤1.2中，将观测序列分为n个状态，即将观测序列d平均分为n份，每份称为一个状态，其中t为整个滑坡演化过程持续时间，t为滑坡灾害发生状态持续时间。

13、优选的，所述步骤2包括：

14、步骤2.1：计算出模型λ的参数，公式具体如下：

15、λ＝(π，a，b，μ(d(st))，σ(d(st))，sfinal)

16、上式中λ为基于gmm-hmm的滑坡时间预测模型，π为初始状态概率分布；a为状态转移概率矩阵；b为观测状态概率分布矩阵；d(st)表示st状态的发生时间；μ(d(st))为gmm函数均值，表征每个状态持续平均时间；σ(d(st))为gmm函数中的方差；sfinal为滑坡发生状态，该状态是通过变形速率所确定；

17、步骤2.2：初始化π，a和b，将观测序列d平均分为n份，每份称为一个状态；采用聚类方法将d的每个状态聚类为m类，并将每类按照高斯混合序号(1，2，...，m)进行编号，得到时间序列ot(t＝1，2，...，n)；

18、步骤2.3：引入扰动因子，构造aspo模型；

19、步骤2.4：利用apso优化参数π、a和b；

20、步骤2.5：优化参数μ(d(st))，σ(d(st))和sfinal。

21、优选的，所述步骤2包括：步骤2.3中，采用停滞步数为触发条件，对个体极值pbest、全局极值gbest和位置更新公式加入扰动因子，扰动方式如下：

22、pbest＝(αt＞t)*pbest                                     (3)

23、gbest＝(βtg＞tg)*gbest                                     (4)

24、x(t+1)＝x(t)+(εto＞to)*v(t+1)                                (5)

25、v(t+1)＝ωv(t)+c1r1(αt＞t*pbest-x(t))+c2r2(βtg＞tg*gbest-x(t))  (6)

26、式(3)和(4)中t、tg分别表示个体极值和全局极值迭代停滞的步数，t、tg表示个体极值和全局极值产生扰动对应的停滞步数的阈值；式(5)中to表示对位置执行扰动操作的次数，to表示位置需要添加扰动对应的阈值；式(6)中c1、c2为学习因子，r1、r2是分布在[0，1]之间的随机数，ω为惯性系数。αt＞t、βtg＞tg和εto＞to为分别对应个体极值pbest、全局极值gbest和位置更新公式三者的扰动因子。x、v分别为粒子位置和粒子速度；扰动因子相关触发条件如下：

27、

28、

29、

30、优选的，步骤2.4中，将每一个粒子对应一个hmm，通过模型迭代，计算相邻两次迭代的hmm的参数π和a的变化情况；定义两个hmm间的距离计算公式如下：

31、

32、上式中以相邻两次迭代欧氏距离差值dx，x+1满足一定要求作为条件，获得更新的π和a；x表示迭代次数，πx表示π更新迭代次数x后的参数，ax表示a更新迭代次数x后的参数，参数b由滑坡位移时序通过高斯分布参数估计公式求得，公式具体如下：

33、

34、

35、上式中bj(ot)是参数b中的具体元素值，j为b中的元素索引值，n为b中的元素个数，即状态数；m为混合高斯数m的任意值，m为加权系数个数，即高斯混合数，ξ(o，μj，m，σj，m)为混合高斯函数，cj，m为加权系数，ot、μj，m和σj，m满足一定要求作为条件分别表示时间序列、m状态下j个元素的平均值和m状态下j个元素的标准差。

36、优选的，步骤2.5中，优化参数μ(d(st))，σ(d(st))和sfinal的公式具体如下：

37、

38、

39、sfinal＝sn

40、其中，l为状态序列的所有位置，l为最后一段状态序列的截取位置，d(st，l)为l区间内出现状态序列st的时间，sn为滑坡的状态序列划分出的第n个状态。

41、优选的，所述步骤3包括：

42、步骤3.1：实时采集数据进行状态解码，判断出其属于滑坡演化中的哪个状态；

43、步骤3.2：采用当前滑坡演化中的状态到达滑坡发生状态的rul估计，预报滑坡灾害可能发生时间，rul为从当前状态到达最后1个滑坡发生状态之间的时间间隔。

44、优选的，所述步骤3.1中，当t＝1时，进行初始化：δ1(i)＝πibi(o1)，i＝1，2，...，n；ψ1(i)＝0；δ1(i)为初始时刻的条件转移概率值，ψ1(i)为初始时刻的转移状态序号；πi、bi和o1分别表示初始状态概率分布矩阵的第i个元素、观测状态概率分布矩阵b的第i个元素和时间序列ot的第一个元素；这里t为整个滑坡演化过程持续时间中滑坡演化完成的时刻，t为滑坡灾害发生状态持续时间中的任一时刻；

45、当t＝2，3，...，t时，结合下式进行递推演算，并记录t时刻的状态i，状态i最可能从t-1的状态j转移而来，aj，i为状态转移概率矩阵a中的具体元素，ot表示时间序列ot的第t个元素；记录t时刻最大的条件转移概率值δt(i)，公式具体如下：

46、

47、同时，记录t时刻最大转移状态序号ψt(i)，公式具体如下：

48、ψt(i)＝argmax[δt-1(j)aj，i]

49、最终通过上述公式得到t时刻最大条件转移概率值p*和最大转移状态序号δt(i)表示t时刻最大的条件转移概率值，具体公式如下：

50、

51、

52、当t＝t-1，t-2，...，1时，通过公式上式确定t时刻最大转移状态序号再利用下式进行回溯，表示t时刻最大转移状态序号：

53、

54、st-l，...，st-2，st-1，st均通过上式回溯确定，将send中数量最多的值作为当前状态scurrent；通过下式求到最优路径send：

55、send＝(st-l，...，st-2，st-1，st)，

56、上式中l为最后一段状态序列的截取位置，t为整个滑坡演化过程持续时间中滑坡演化完成的时刻。

57、优选的，所述步骤3.2中，对新测试数据进行状态解码和rul计算，将状态值带入下式中，μ(d(st))为gmm函数均值，表征每个状态持续平均时间，利用dijkstra算法得到scurrent到达sfinal的最短时间，能算出rul，具体公式如下：

58、

59、apso-hmm模型训练完成后，若合位移速率超过安全阈值，则通过上述步骤给出滑坡的估计发生时间，同时启动报警机制；否则继续监控。

60、本发明具有以下优点：

61、1、本发明根据以往的数据去预测未来的数据情况，解决了以往检测设备只能实时监测，不能预测数据的局限，不仅可以实时监测，精度高，而且时效性强。

62、2、本发明通过分段数据的高斯混合特性，重构位移数据演化过程的所属状态；

63、3、本发明提出一种引入扰动因子的自适应粒子群算法aspo，并将该方法应用于隐马尔科夫模型的训练，实现对隐马尔科夫模型初始参数的优化。

64、4、当确定出最终突变状态后，利用最优路径算法，计算出从当前状态到达最终突变状态的最短时间，从而预报滑坡灾害发生的时间。

65、5、本发明使用范围广：不需要增加额外的辅助信息，该方法可广泛应用于滑坡、地面沉降和地裂缝等重点地质灾害隐患类型，具有广阔的应用前景。