不确定环境下人脸表情分类的鲁棒自适应更新方法

1.本发明涉及图像分类的技术领域，具体涉及不确定环境下人脸表情分类的鲁棒自适应更新方法。


背景技术：

2.卷积神经网络以独特的优势应用于图像分类中，通过学习训练样本与参考样本之间的特征组合关系，并不断更新权重参数，完成分类工作。但当待测试对象发生变化，输入图像出现信息丢失，原有网络模型参数不能自适应更新，原有网络权重参数在发生改变后的数据集上应用效果差，此时网络需要重新训练，这使得网络模型的参数确定成为非常耗时的任务。为了达到更好的分类效果，cheng等人提出，通过rpca增加变量的权重来提取图像深层特征。到2016年，jiang提出信息熵的方法，yij提出的变换算子方法，来进行特征加权和改变协方差矩阵空间变化。2017年，xux提出模块主元分析算法，通过类内加权平均值提升图像分类性能。
3.但是系统模态发生改变时，原有的网络模型参数直接对新样本操作，将导致表情图像分类性能降低，导致网络权重参数将需要反复训练，因此，我们应该针对该问题进一步研究。


技术实现要素：

4.鉴于现有技术的不足，本发明旨在于不确定环境下人脸表情分类的鲁棒自适应更新方法。
5.为了实现上述目的，本发明采用的技术方案如下：
6.不确定环境下人脸表情分类的鲁棒自适应更新方法，所述方法包括：先引入平均影响值算法，联合多维泰网分类层和偏导加权算法，通过非线性拟合函数对特征变量的偏导运算，筛选出重要特征节点，并以此分配权重系数；然后，利用卡尔曼滤波方法以已有的参数为初始值，对网络模型中的特征参数进行自适应更新，在不需要反复训练网络权重参数的基础上，实现差异更新网络权重参数；最后，利用更新后的网络对信息缺失表情图像进行分类。
7.需要说明的是，基于偏导加权的参数筛选方法中，对非线性拟合函数的某变量求偏导表示如下：
[0008][0009]
令δ
·
xi(w)＝δxi，则有
[0010][0011]
其中，δ表示关于第i个分量的扰动比率。
[0012]
当δxi→
0时，则平均影响值算法的最优权值为变量求偏导算法的结果，如下式所示：
[0013][0014]
δxi表示第i个分量围绕它xi(w)自身的正负扰动量；ivi第i个分量受xi(w)自身的正负扰动量后的输出增量；
[0015]
求平均；是关于第i个分量的求取偏导数。
[0016]
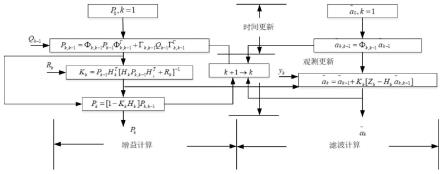
需要说明的是，提取以多维泰勒网络为分类器系统的权重参数w和偏置参数b；网络输出的卡尔曼滤波形式如下式：
[0017][0018]
其中，xi是输入层第i个神经元的输入；确定网络更新参数的状态模型与观测模型，如下式，以此实现对分类器参数的更新。
[0019]
y(k)＝h(k)x(k)+r(k)
[0020][0021]
x(k)＝f(k-1)x(k-1)+q(k-1)
[0022]
其中，α表示各特征对输出的影响值，x(k)∈rn×1是系统的n个状态，状态转移矩阵为f(k-1)∈rn×n，系统过程噪声为q(k-1)；传感器矩阵为h(k)∈rm×n，传感器向量为y(k)∈rm×1，系统的测量噪声用r(k)表示；q(k)和r(k)是q(k-1)与r(k)分别其对应均值差的平方和。
[0023][0024]
然后，假设滤波初始估计值为k表示新批次索引，设初始误差协方差为p(k-1|k-1)。
[0025]
需要说明的是，对新样本而言，通过下面计算步骤完成卡尔曼滤波递推过程：
[0026]
s1利用初始估计值和状态转移矩阵计算出下一步预测值
[0027][0028]
s2计算出预测误差协方差矩阵
[0029]
p(kk-1)＝f(k-1)p(k-1k-1)f
t
(k-1)+q(k-1)
[0030]
s3计算卡尔曼增益矩阵
[0031]
k(k)＝p(k|k-1)h
t
(k)[h(k)p(kk-1)h
t
(k)+r(k)]-1
[0032]
s4计算状态估计值
[0033][0034]
s5计算出误差协方差矩阵
[0035]
p(k|k)＝(i-k(k)h(k))p(k|k-1)(i-k(k)h(k))
t
+k(k)r(k)k
t
(k)
[0036]
重复s1-s5，实现待估参数的迭代更新。
[0037]
本发明有益效果在于：
[0038]
针对传统的网络优化算法不能在系统改变时，自适应更新网络模型参数的问题，本发明引入卡尔曼滤波器进行参数更新，同时，由于表情图像在不同噪声干扰下丢失信息的程度不同，以及丢失信息的重要性不一致，考虑到不同的特征点对分类结果的影响程度不同。直接利用miv加权算法，会由于增量系数的人为选取，导致权重因子最优值的选取出现偏差。本发明提出联合多维泰勒网分类层和偏导加权算法，通过对非线性拟合函数对特征变量的偏导运算，筛选重要特征节点，并以此给每个特征节点赋予影响权重，然后，更新带有影响权重的特征数据，有差异的对权重参数进行在线更新。最后在新模型参数下实现对噪声样本的分类。本发明可在不改变网络模型其他参数的情况下，避免网络模型全部参数的重复训练，在不影响分类性能的同时，实现分类器参数的差异更新，并减少计算机存储空间。
附图说明
[0039]
图1为本发明经过卡尔曼滤波参数更新的示意图；
[0040]
图2为本发明仿真试验中图像信息丢失比例分别为5％的示意图；
[0041]
图3为本发明仿真试验中图像信息丢失比例分别为10％的示意图
[0042]
图4为本发明仿真试验中图像信息丢失比例分别为15％的示意图；
[0043]
图5为本发明仿真试验中图像信息丢失比例分别为20％的示意图。
具体实施方式
[0044]
下将结合附图对本发明作进一步的描述，需要说明的是，本实施例以本技术方案为前提，给出了详细的实施方式和具体的操作过程，但本发明的保护范围并不限于本实施例。
[0045]
需要指出的是，本发明的平均影响值算法(meanimpactvalue，miv)是通过判断对输出的平均影响程度，来筛选重要特征。miv值的符号表示影响的相关方向，数值表示影响的程度大小，iv表示影响值，miv表示多次实验并对影响值取平均。
[0046]
本发明为不确定环境下人脸表情分类的鲁棒自适应更新方法，所述方法包括：先
引入平均影响值算法，联合多维泰网分类层和偏导加权算法，通过非线性拟合函数对特征变量的偏导运算，筛选出重要特征节点，并以此分配权重系数；然后，利用卡尔曼滤波方法以已有的参数为初始值，对网络模型中的特征参数进行自适应更新，在不需要反复训练网络权重参数的基础上，实现差异更新网络权重参数；最后，利用更新后的网络对信息缺失表情图像进行分类。
[0047]
需要说明的是，基于偏导加权的参数筛选方法中，对非线性拟合函数的某变量求偏导表示如下：
[0048][0049]
令δ
·
xi(w)＝δxi，则有
[0050][0051]
其中，δ表示关于第i个分量的扰动比率。
[0052]
当δxi→
0时，则平均影响值算法的最优权值为变量求偏导算法的结果，如下式所示：
[0053][0054]
δxi表示第i个分量围绕它xi(w)自身的正负扰动量；ivi第i个分量受xi(w)自身的正负扰动量后的输出增量；
[0055]
求平均；是关于第i个分量的求取偏导数。
[0056]
需要说明的是，提取以多维泰勒网络为分类器系统的权重参数w和偏置参数b；网络输出的卡尔曼滤波形式如下式：
[0057][0058]
其中，xi是输入层第i个神经元的输入；确定网络更新参数的状态模型与观测模型，如下式，以此实现对分类器参数的更新。
[0059]
y(k)＝h(k)x(k)+r(k)
[0060][0061]
x(k)＝f(k-1)x(k-1)+q(k-1)
[0062]
其中，α表示各特征对输出的影响值，x(k)∈rn×1是系统的n个状态，状态转移矩阵
为f(k-1)∈rn×n，系统过程噪声为q(k-1)；传感器矩阵为h(k)∈rm×n，传感器向量为y(k)∈rm×1，系统的测量噪声用r(k)表示；q(k)和r(k)是q(k-1)与r(k)分别其对应均值差的平方和。
[0063][0064]
然后，假设滤波初始估计值为k表示新批次索引，设初始误差协方差为p(k-1|k-1)。
[0065]
需要说明的是，对新样本而言，通过下面计算步骤完成卡尔曼滤波递推过程：
[0066]
s1利用初始估计值和状态转移矩阵计算出下一步预测值
[0067][0068]
s2计算出预测误差协方差矩阵
[0069]
p(k|k-1)＝f(k-1)p(k-1|k-1)f
t
(k-1)+q(k-1)
[0070]
s3计算卡尔曼增益矩阵
[0071]
k(k)＝p(k|k-1)h
t
(k)[h(k)p(kk-1)h
t
(k)+r(k)]-1
[0072]
s4计算状态估计值
[0073][0074]
s5计算出误差协方差矩阵
[0075]
p(kk)＝(i-k(k)h(k))p(kk-1)(i-k(k)h(k))
t
+k(k)r(k)k
t
(k)
[0076]
重复s1-s5，实现待估参数的迭代更新。
[0077]
实施例
[0078]
通过以下仿真实验为了验证本发明的方法的性能。
[0079]
fer2013数据集中，生气标签在训练集中有3196张样本，在测试集中有799张样本；厌恶标签在训练集中有348张样本，在测试集中有88张样本；恐惧标签在训练集中有3277张样本，在测试集中有820张样本；高兴标签在训练集中有5772张样本，在测试集中有1443张样本；悲伤标签在训练集中有3864张样本，在测试集中有966张样本；惊讶标签在训练集中有2536张样本，在测试集中有635张样本；中性标签在训练集中有3972张样本，在测试集中有993张样本。以此数据集为基础，训练深度残差卷积自编码模型，以及以多维泰勒网为基础的分类器。然后，提取多维泰勒网分类器中对应的权重和偏置，通过卡尔曼滤波方法对分类器参数更新，使用更新后的网络参数，对噪声面部表情图像数据集进行分类。混淆矩阵实验结果如图2-图5所示。
[0080]
由混淆矩阵可得，在fer2013数据集中，高兴与惊讶类别的识别率比其他高。而由于悲伤与害怕两种表情相似，这导致两种类别识别率最低。对于高兴与惊讶类别，经参数更新后比未经参数更新的识别率，在信息丢失5％时可以提高5％和8％。在信息丢失10％时可以提高6％和7％。在信息丢失15％时可以提高9％和7％。在信息丢失20％时可以提高4％和5％。因此可以得出，经过本章提出的参数更新方法，可以明显提高信息丢失时分类精度。运行20次，取多次实验结果平均数并保留两位有效数字，汇总实验数据如下表所示：
[0081][0082]
由上表的数据可知，使用卡尔曼滤波算法差异更新多维泰勒网络层的权重参数，可以有效解决由于像素信息丢失造成分类效率低的问题。使用卡尔曼滤波方法更新参数权重，丢失5％像素信息时，分类准确率可以提高10.88％。丢失10％像素信息时，分类准确率可以提高9.44％。丢失15％像素信息时，分类准确率可以提高10.45％。丢失20％像素信息时，分类准确率可以提高17.84％。
[0083]
对于本领域的技术人员来说，可根据以上描述的技术方案以及构思，做出其它各种相应的改变以及变形，而所有的这些改变以及变形都应该属于本发明权利要求的保护范围之内。