一种图像识别方法、系统和存储介质与流程

1.本发明涉及模式识别和人工智能领域，尤其涉及一种图像识别方法、系统和存储介质，该方法基于四元数广义核稀疏主成分分析。


背景技术：

2.研究表明，目前，彩色医疗图像识别是模式识别领域的重要研究课题之一。jia等给出的二维四元数主成分分析(two dimensional quaternion principal component analysis,简称2dqpca)通过直接处理二维四元数矩阵解决了二维样本被拉成向量的形式导致计算成本高，且失去了彩色图像所固有的空间结构的问题[z.jia,s.ling and m.zhao.color two-dimensional principal component analysis for face recognition based on quaternion model[j].springer,cham,2017.]，但这个方法无法处理非线性特征问题。于是，chen利用核函数将四元数主成分分析改进为核四元数主成分分析(kernel quaternion principal component analysis,简称kqpca),将线性四元数信号转化为非线性四元数信号[b.chen,j.yang,b.jeon and x.zhang.kernel quaternion principal component analysis and its application in rgb-d object recognition[j].neurocomputing,266:293-303,2017.]。这些方法，虽然能充分利用四元数的四个通道，但是都没有考虑到四元数的计算效率、稳定性以及图像中元素的熵，这导致在实际应用效果不是很理想。比如，这些方法局限于特殊场景下人脸识别的应用，对黑色背景下的医疗图像识别率无法达到工程要求，此外，医疗图像的水雾、图像亮度、病灶颜色、电流噪声等复杂多变的干扰特征，现有的2dqpca，kqpca等方法的有限特征无法表征海量病灶数据。
[0003]
为了能从含噪声、雾气等干扰因素的医疗图像中提取核稀疏主成分，具有稀疏特征的二维主成分分析在计算机图像识别和分类领域引起了广泛的关注。xiao充分利用一范数约束项和二范数约束项的优点提出了稀疏二维四元数主成分分析(sparse two dimensional quaternion principal component analysis,简称s2dqpca)模型,提高了分类的鲁棒性[x.xiao,z.yi.two-dimensional quaternion pca and sparse pca[j].ieee transactions on neural networks and learning systems,30:2028-2042,2018.]。但该模型仍然存在一些问题尚未解决，首先，该模型将四元数转化为复数进行运算，增加了计算成本，这导致训练样本特征和测试样本的时间过长，无法实时进行数据特征更新和样本的识别；其次，该模型局限于人脸识别工作，无法利用核函数来处理非线性特征，在应对医疗图像时经常出现病灶特征相似但类型异同的识别过程中，不能准确识别出正确图像类别；最后，该模型对不同的数据样本，需要人工调整参数，限制了算法的应用价值。


技术实现要素：

[0004]
本发明的目的在于提供一种图像识别方法、系统和存储介质，所述方法和系统都是基于四元数广义核稀疏主成分分析，旨在解决现有技术中计算成本高、识别率低且不稳定、需要人工调参等问题。
[0005]
为了实现上述发明目的，本发明提供一种图像识别方法，基于四元数广义核稀疏主成分分析，所述方法包括步骤：获取训练样本集和测试样本集图像；提取每幅训练样本图像的熵、红、绿、蓝四个分量信息，并对其进行四元数矩阵表示，以构造与之对应的四元数实表示矩阵；根据所述四元数实表示矩阵，构建该四元数实表示矩阵的四元数协方差核矩阵和四元数p范数欧氏距离，其中p是任意非负值；根据所述四元数协方差核矩阵和四元数p范数欧式距离，构建四元数广义核稀疏主成分分析优化模型；对所述优化模型求解，将计算得到的训练样本行、列方向的核稀疏主成分作为其最终解；根据所述模型行、列方向的核稀疏主成分，分别计算所述训练样本四元数协方差核矩阵的投影矩阵和测试样本四元数协方差核矩阵的投影矩阵；基于所述四元数p范数欧式距离，根据所述投影矩阵识别测试样本集中图像所属的类别；输出所述图像类别。
[0006]
作为本发明的进一步改进，所述“提取每幅训练样本图像的熵、红、绿、蓝四个分量信息”步骤之前还包括：对样本集中的每幅图像都表示为固定大小的矩阵，其中，所述样本集包括训练样本集和测试样本集。
[0007]
作为本发明的进一步改进，所述“提取每幅训练样本图像的熵、红、绿、蓝四个分量信息，并对其进行四元数矩阵表示，以构造与之对应的四元数实表示矩阵”具体包括：提取第n张样本图像对应的熵、红、绿、蓝四个分量信息，分别记为en、rn、gn、bn，其中n＝1，2，...，l，l是所述训练样本集中的图像个数；根据所述四个分量信息，该样本图像的四元数矩阵表示为：pn＝en+rni+gnj+bnk，其中，pn∈qh×w为第n个四元数矩阵，h
×
w是训练样本图像对应的矩阵大小，i、j、k表示四元数的三个虚单元；利用四元数保结构理论构造所述四元数矩阵pn的实表示矩阵mn。
[0008]
作为本发明的进一步改进，所述“构建该四元数实表示矩阵的四元数协方差核矩阵和四元数p范数欧氏距离”具体包括：根据所述训练样本集和测试样本集，构建对应的四元数实表示矩阵，记为x
train
和x
test
；将所述四元数实表示矩阵投影到高维四元数特征空间中，以计算该训练样本集和测试样本集的四元数协方差核矩阵，分别表示为：其中，表示由x
train
投影以后的训练图像，表示为的共轭转置矩阵，表示由x
test
投影以后的测试图像，表示为的共轭转置矩阵；所述四元数矩阵的实表示矩阵mn的p范数欧氏距离为：的p范数欧氏距离为：其中，非负参数p代表所述四元数p范数，en、rn、gn、bn分别代表四元数的一个实部和三个虚部。
[0009]
作为本发明的进一步改进，所述“构建四元数广义核稀疏主成分分析优化模型”具体包括：定义训练样本行、列方向的核稀疏主成分矩阵：u＝[u1，
…
，uk]∈q
4t
×
4t
，v＝[v1，
…
，vs]∈q
4t
×
4t
，u和v都是分别由k列和s列四元数特征向量组成的；对于任意的非负参数μ1，μ2，λ3，λ4和μi(1≤i≤k)，λm(1≤m≤s)，若所述行列核稀疏主成分矩阵u和v满足：(1≤m≤s)，若所述行列核稀疏主成分矩阵u和v满足：(1≤m≤s)，若所述行列核稀疏主成分矩阵u和v满足：(1≤m≤s)，若所述行列核稀疏主成分矩阵u和v满足：则
其中，w是权重系数，和是分别对φ
rtrain
和φ
ctrain
进行四元数cholesky分解的结果，φ
rtrain
表示按行方向计算得到的四元数协方差核矩阵，φ
ctrain
表示按列方向计算得到的四元数协方差核矩阵，分别表示寻找k个最优ui和s个最优vm使得所述模型的散度最大化，参数μi和λm分别表示对该模型行、列方向的散度调整。
[0010]
作为本发明的进一步改进，所述方法还包括：对所述四元数广义核稀疏主成分分析优化模型求解采用了基于交替方向乘子法的四元数保结构算法。
[0011]
作为本发明的进一步改进，所述方法还包括：所述基于交替方向乘子法的四元数保结构算法选取的迭代初始值采用随机生成满足正态分布的数据作为迭代初始值或基于四元数实表示的幂法与反幂法循环迭代得到的数据作为迭代初始值。
[0012]
作为本发明的进一步改进，所述“根据所述模型行、列方向的最终解，分别计算所述训练样本四元数协方差核矩阵的投影矩阵和测试样本四元数协方差核矩阵的投影矩阵”具体包括：所述训练样本四元数协方差核矩阵φ
train
的投影矩阵其中，j＝1，2，...，t，v＝1，2，...，k，k表示训练样本集的前k个核稀疏主成分；所述测试样本四元数协方差核矩阵φ
rest
的投影矩阵其中，g＝1，2，...，m，m表示测试样本集的前m个核稀疏主成分。
[0013]
作为本发明的进一步改进，所述“利用所述四元数p范数欧式距离以识别测试样本集中图像所属类型”具体包括：根据所述训练样本四元数协方差核矩阵的投影矩阵找到与所述测试样本四元数协方差核矩阵的投影矩阵p
test
最接近的训练样本四元数协方差核矩阵的投影矩阵使其满足以确定测试样本集中图像的类别c，其中，为所述四元数p范数的欧式距离，p可根据不同的待测图像进行相应调整。
[0014]
本发明还提供一种图像识别系统，基于四元数广义核稀疏主成分分析，所述系统包括处理器和存储介质；所述存储介质用于存储指令；所述处理器用于根据所述指令进行操作以执行任意一项所述基于四元数广义核稀疏主成分分析的图像识别方法的步骤。
[0015]
本发明还提供一种存储介质，所述存储介质存储有计算机程序，所述计算机程序被处理器执行时实现如上任意一项所述基于四元数广义核稀疏主成分分析的图像识别方法。
[0016]
与现有技术相比，本发明基于四元数广义核稀疏主成分分析的图像识别方法带来的有益效果如下：
[0017]
1.本发明利用四元数对彩色图像的熵、红、绿、蓝四个分量信息进行表征，构造出四元数实表示形式矩阵，解决了图像像素熵信息丢失问题。
[0018]
2.本发明基于四元数实表示矩阵得到四元数协方差核矩阵，利用四元数p范数欧式距离构建四元数广义核稀疏主成分分析优化模型(qgkspca)，该模型能从含有噪声样本中准确提取核稀疏主成分，从而保证了对含有噪声的彩色医疗图像也能成功识别的效果。
[0019]
3.本发明在构建所述优化模型时，将训练样本的行、列方向的最大投影散度联系
在一起计算模型散度的最大化，并能灵活调节行列方向之间的关系，体现了双边性，即考虑了训练样本所有方向的特征，保证了所述优化模型方法的合理性和识别精度的可靠性。
[0020]
4.本发明构建的p范数欧式距离中的p值是可调的任意非负数，能体现广义的特征。因此在样本图像特征提取时能针对噪声、亮度、雾气等干扰因素灵活调节p，不仅防止训练过拟合，即保证识别效率的稳定性，而且p的可调性也保证了所述模型方法能针对各种复杂多变的医疗图像进行识别，适用性高。
[0021]
5.本发明采用基于四元数保结构算法的交替方向乘子法，计算时间更短、内存占用少、计算成本低。
附图说明
[0022]
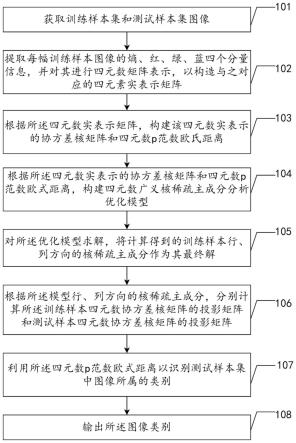
图1是本发明实施例中四元数广义核稀疏主成分分析的图像识别方法步骤流程图。
[0023]
图2是本发明实施例中基于四元数广义核稀疏主成分分析的图像识别方法的流程示意图。
[0024]
图3是本发明实施例中四种彩色医疗图像识别方法计算得到的正确率随着核稀疏主成分个数变化而变化的曲线示意图。
[0025]
图4是本发明实施例中彩色医疗图像数据库下权重系数w随着核稀疏主成分个数变化的三维曲线的示意图。
具体实施方式
[0026]
以下将结合附图所示的具体实施方式对本发明进行详细描述。但这些实施方式并不限制本发明，本领域的普通技术人员根据这些实施方式所做出的结构、方法、或功能上的变换均包含在本发明的保护范围内。
[0027]
需要说明的是，术语“包括”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。此外，术语“第一”、“第二”等仅用于描述目的，而不能理解为指示或暗示相对重要性。
[0028]
本技术公开了一个实施方式的一种图像识别方法，基于四元数广义核稀疏主成分分析，虽然本技术提供了如下述实施方式或流程图1所述的方法操作步骤，但是基于常规或者无需创造性的劳动，所述方法在逻辑性上不存在必要因果关系的步骤中，这些步骤的执行顺序不限于本技术实施方式中所提供的执行顺序。如图1所示，本发明实施例提供了一种基于四元数广义核稀疏主成分分析的图像识别方法，所述方法包括以下若干步骤，下面对所述方法及每个步骤分别进行说明：
[0029]
步骤101，获取训练样本集和测试样本集图像。
[0030]
步骤102，提取每幅训练样本图像的熵、红、绿、蓝四个分量信息，并对其进行四元数矩阵表示，以构造与之对应的四元数实表示矩阵。
[0031]
在本发明实施例中，获取含有噪声的样本集，从中随机选取t个训练样本集和l-t个测试样本集，分别记作tr和te。将所述样本集中的l个彩色图像都先调整为固定大小的矩阵，比如将样本图像都调整为h
×
w固定大小的矩阵，其中，h为图像的高度，w为图像的宽度。
对每个样本图像都做特征提取操作，具体的，假设提取第n张样本图像对应的熵、红、绿、蓝四个分量信息，分别简记为en，rn，gn，bn，其中n＝1，2，
…
，l，并对其进行按照公式(1)进行四元数矩阵表示：
[0032]
pn＝en+rni+gnj+b
nkꢀꢀ
(1)
[0033]
其中，pn∈qh×w为第n个四元数矩阵，即矩阵pn属于四元数矩阵，并且该四元数矩阵的大小为h行w列，i，j，k表示四元数矩阵的三个虚单位。
[0034]
在本发明实施例中，根据所述四元数矩阵表示，利用四元数保结构理论构造每个四元数矩阵pn的实表示矩阵mn，具体的如公式(2)所示：
[0035][0036]
其中n＝1，2，
…
，l，r表示实数域，mn∈r
4h
×
4w
表示四元数实表示矩阵mn属于实数域矩阵，且实数域矩阵大小是4h
×
4w，也就是说四元数实表示矩阵得到的结果都是实数，没有虚数，降低了后续计算过程的时间和成本，提高了计算效率。
[0037]
步骤103，根据所述四元数实表示矩阵，构建该四元数实表示矩阵的四元数协方差核矩阵和四元数p范数欧氏距离。
[0038]
在本实施例的步骤101和102中已经获得了四元数实表示矩阵，具体的，假设将t个训练样本和l-t个测试样本的四元数矩阵实表示，简记为x
train
和x
test
，并对其进行中心化，统一其计算指标，避免因计算指标的不一致而导致计算结果得错误。
[0039]
在本发明实施例中，为了更好的提取训练样本图像的特征，本发明将样本特征空间投影到高维四元数空间，引入了核函数，通过用核函数把输入的训练样本图像特征矩阵投影到高维特征空间，从而将线性问题转换成非线性问题，使得提取出图像特征更准确。具体的，定义四元数映射ψ：将四元数空间矩阵qm中的矢量数据投影到高维四元数特征空间g中，ψ：qm→
g，其中x表示训练样本图像，表示映射到高维空间以后的图像。在投影后，根据公式(3)和公式(4)计算出所述训练样本集和测试样本集的四元数协方差核矩阵，公式(3)和(4)分别为：
[0040][0041][0042]
其中，表示由x
train
投影以后的训练样本图像，表示为的共轭转置矩阵，表示由x
test
投影以后的测试样本图像，表示为的共轭转置矩阵。
[0043]
根据公式(1)所述的四元数矩阵，使用公式(5)定义四元数实表示矩阵mn的p范数欧式距离，为后续的模型构建奠定基础。公式(5)的具体定义如下所示：
[0044][0045]
其中，en，rn，gn，bn分别代表四元数矩阵的一个实部和三个虚部，非负参数p代表四元数p范数。
[0046]
步骤104，根据所述四元数协方差核矩阵和四元数p范数欧式距离，构建四元数广
义核稀疏主成分分析优化模型。
[0047]
在本发明实施例中，根据步骤103定义的四元数实表示矩阵的p范数欧式距离，构建所述优化模型的具体过程如下：
[0048]
首先定义两个四元数实表示矩阵u＝[u1，
…
，uk]∈q
4t
×
4t
，v＝[v1，
…
，vs]∈q
4t
×
4t
是分别由k列和s列四元数特征向量组成的，其中u表示训练样本行方向的核稀疏主成分，v表示训练样本列方向的核稀疏主成分，对于任意的非负参数μ1，μ2，λ3，λ4和μi(1≤i≤k)，λm(1≤m≤s)，若所述u＝[u1，
…
，uk]∈q
4t
×
4t
，v＝[v1，
…
，vs]∈q
4t
×
4t
满足公式(6)时，则公式(6)具体如下所示：
[0049][0050]
其中，w是权重系数，用于防止单独计算行和列方向投影值无法获取的最优解，权重w将行方向和列方向的最大投影散度联系在一起计算，并能通过调节权重的大小来调整两个方向投影值之间的关系，体现了双边性，从而考虑了训练样本图像所有方向的特征，从而保证了所述模型方法的合理性和识别图像类别的准确性以及可靠性，使得计算出的核稀疏主成分特征矩阵更贴合彩色图像特征。和是分别对φ
rtrain
和φ
ctrain
进行四元数cholesky分解的结果，而φ
rtrain
表示在投影后，训练集样本图像按照行方向计算得到的四元数协方差核矩阵，φ
ctrain
表示在投影后，训练集样本图像按照列方向计算得到的四元数协方差核矩阵，保持了行方向核稀疏矩阵解的正交性，同理列方向核稀疏矩阵vm解也是一样。
[0051]
在本实例的公式(6)中的他分别表示寻找k个最优ui和s个最优vm使得所述模型的散度最大化，参数μi和λm分别表示对行、列方向的散度调整，具体的，和用于应对不同噪声环境的自适应调整，p值是可调的任意非负值，所以本发明构造的模型方法在提取特征是能针对噪声、亮度、雾气等干扰因素灵活调节，不仅保证了对各种复杂多变的医疗彩色图像进行识别，而且通过灵活调整p可以防止训练过拟合，即保证了图像识别效率的稳定性。另外，优选的，本发明中的p可以按0.1为步长大小，通过设置识别精度最大值循环迭代算法，解决训练时手动调整参数p的繁琐过程。μ2和λ4用于控制u和v的非零元个数，即ui解的稀疏性。
[0052]
另外，公式(6)中的||ui||1和|vm||1体现了本发明实施例提取了训练样本图像的核稀疏主成分，即能从含噪声样本中准确提取特征，从而保证了所述模型能对成功识别含噪声的彩色医疗图像。
[0053]
步骤105，对所述优化模型求解，将计算得到的训练样本行、列方向的核稀疏主成
分作为其最终解。
[0054]
在本发明实施例中，根据所述优化模型的构造过程，对其进行求解，具体包括如下步骤：
[0055]
step1，考虑每个样本第i个分量ui和每个第m个分量vm，采用循环迭代的方法可获得全部的解u＝[u1，
…
，uk]∈q
4t
×
4t
，v＝[v1，
…
，vs]∈q
4t
×
4t
，因此对所述公式(6)进行优化，得到公式(7)，具体如下所示：
[0056][0057]
step2，引入中间变量zi(1≤i≤k)和wm(1≤m≤s)，建立四元数实表示增广拉格朗日函数并简化为公式(8)所示的：
[0058][0059]
其中i＝1，2，
…
，k,m＝1，2，
…
，s，
[0060]
step3，利用交替方向乘子法对公式(8)进行迭代求解，在每次迭代循环中，将ui，mi，zi，lm，vm，tm分为两组，ui，mi，zi记为a组，lm，vm，tm记为b组。然后分别只更新a组合和b组中的其中一个变量，两外两个变量保持固定。具体的，更新a组中的ui，固定a组中的mi，zi，同时更新b组中的vm，固定b组中的lm，tm，得到ui和vm，具体如公式(9)和(10)所示：
[0061][0062][0063]
其中i＝1，2，
…
，k，m＝1，2，
…
，s，i表示大小为4h
×
4w的单位矩阵，φ
train
是公式(6)中的四元数协方差核矩阵，ρ1与ρ2是公式(8)的惩罚参数。
[0064]
step4，更新a组中的zi，固定a组中的ui，mi，同时更新b组中的lm，固定b组中的vm，tm，计算得到zi和lm，具体如公式(11)和(12)所示：
[0065][0066][0067]
其中i＝1，2，
…
，k，m＝1，2，
…
，s。
[0068]
step5，更新a组中的mi，固定a组中的ui，zi。同时更新b组中的tm，固定b组中的vm，lm，得到mi和tm，具体如公式(13)和(14)所示：
[0069][0070][0071]
其中i＝1，2，
…
，k，m＝1，2，
…
，s，k∈[0，+∞)，表示mi随机生成的非零值，表示tm随机生成的非零值，表示mi第k+1次迭代的结果，表示tm第k+1次迭代的结果，表示mi第k次迭代的结果，表示tm第k次迭代的结果。
[0072]
在本发明实施例中，根据step5步骤得到的公式(13)和(14)可知，在选取迭代初始值时，有两种方案可供选择。一种是通过随机生成满足正态分布的数作为ui，mi，zi，lm，vm，tm的初值。另外一种是利用四元数实表示矩阵的幂法和反幂法循环迭代得到迭代初始值。然后设置最大识别精度阈值，当其迭代达到最大识别精度阈值时停止迭代，使得识别精度达到最大的对应核稀疏主成分作为所述模型的最终解和
[0073]
步骤106，根据所述模型行、列方向的核稀疏主成分，分别计算所述训练样本四元数协方差核矩阵的投影矩阵和测试样本四元数协方差核矩阵的投影矩阵。
[0074]
在本发明实施例中，步骤101-105是样本训练的过程，通过训练构建了四元数广义核稀疏主成分分析优化模型(qgkspca)并求解出对应的核稀疏主成分和作为该模型的最终解，再根据公式(15)和(16)进一步计算训练样本协方差核矩阵和测试样本协方差核矩阵在行列方向的投影矩阵，公式(15)和(16)如下所示：
[0075][0076][0077]
其中，j＝1，2，...，t，v＝1，2，
…
，k,g＝1，2，
…
，m，k表示训练样本集的前k个核稀疏主成分，m表示测试样本集的前m个核稀疏主成分。p
train
是训练样本四元数协方差核矩阵φ
train
的投影矩阵，p
test
是测试样本四元数协方差核矩阵φ
test
的投影矩阵。
[0078]
步骤107，利用所述四元数p范数欧式距离以识别测试样本集中图像所属的类别。
[0079]
步骤108，输出所述图像类别。
[0080]
在本发明实施例中，利用四元数p范数欧式距离进行测试样本集中图像的识别，具体的，通过计算与测试样本四元数协方差核矩阵的投影矩阵最接近的训练样本四元数协方差核矩阵的投影矩阵使其满足公式(17)：
[0081][0082]
公式(17)中的为公式(8)中定义的四元数p范数的欧式距离，以此确定测试样本集中图像的类别c并输出。具体的，在本实施例中，当0＜p＜1时，四元数广义核稀疏主成分分析优化模型(qgkspca)变为一个凹模模型，而当p≥1时，四元数广义核稀疏主成分分析优化模型(qgkspca)变为一个凸模型，因此，采用可调的p值，更利用对彩色图像进行识别，也更加能说明识别过程的合理性。
[0083]
图2所示的是基于四元数广义核稀疏主成分分析的图像识别方法的流程图，利用
四元数对彩色图像的熵、红、绿、蓝四个信息进行表征，构造出四元数实表示形式矩阵；其次基于四元数实表示矩阵构建行方向和列方向的四元数协方差核矩阵，并对四元数协方差核矩阵进行四元数cholesky分解，再利用四元数p范数欧式距离构建四元数广义核稀疏主成分分析优化模型(qgkspca)；接着采用基于交替方向乘子法的四元数保结构解法提取该模型的核稀疏特征解，该模型可以从含多类噪声的训练样本中提取关键特征，利用可灵活调整的权重系数w和四元数p范数，基于四元数保结构算法，准确计算出行列方向的核稀疏主成分结构。再后来根据核稀疏主成分结构分别计算训练样本四元数协方差核矩阵的投影矩阵和测试样本四元数协方差核矩阵的投影矩阵，最后利用四元数实表示的p范数欧式距离对待测试图像进行识别，输出对应的类别。
[0084]
图3所示的是四种彩色医疗图像识别方法计算得到的正确率随着核稀疏主成分个数变化而变化的曲线，横坐标表示的是核稀疏主成分个数，纵坐标表示的是图像识别的准确率。所述的四种图像识别方法分别是列方向占主导的四元数广义核稀疏主成分分析(qgkspcacol)、二维四元数主成分分析(2dqpca)、核四元数主成分分析(kqpca)和行方向占主导的四元数广义核稀疏主成分分析(qgkspcarow)。
[0085]
具体的，图3是将上述四种方法在含噪声彩色图像数据的识别效果进行对比，本发明提出的列方向占主导的四元数广义核稀疏主成分分析(qgkspcacol)和行方向占主导的四元数广义核稀疏主成分分析(qgkspcarow)这两种方法最高识别率分别为0.92和0.91，在图像识别率上优于其他现有的算法。在图3中当提取核稀疏主成分个数超过5后，本发明所述的四元数广义核稀疏主成分分析模型(qgkspca)识别精度一直保持稳定，而对比现有的核四元数主成分分析(kqpca)方法，由于无法提取精确的核稀疏主成分，所以当提取核稀疏主成分个数为18时，识别的准确率降到0.39。本实施例说明，本发明所述的四元数广义核稀疏主成分分析模型(qgkspca)可以在含噪声、亮度、雾气等干扰的医疗图像中，提取和计算精确核稀疏主成分特征，提高了对彩色图像的识别准确率和鲁棒性。
[0086]
图4是本发明实施例中彩色医疗图像数据库下权重系数w随着核稀疏主成分个数变化的三维曲线的示意图。权重系数w的取值范围是(0,1)，w将行列方向的最大投影散度联系在一起计算，并能灵活调节行、列方向两者关系体现了双边性，即考虑了样本所有方向的特征，从而使得图像识别精度的可靠性。
[0087]
本发明实施例还提供了一种图像识别系统，基于四元数广义核稀疏主成分分析，所述系统包括处理器和存储介质；所述存储介质用于存储指令；所述处理器用于根据所述指令进行操作以执行任意一项所述基于四元数广义核稀疏主成分分析的图像识别方法的步骤。
[0088]
本发明实施例还提供了一种存储介质，所述存储介质存储有计算机程序，所述计算机程序被处理器执行时实现如上任意一项所述的基于四元数广义核稀疏主成分分析的图像识别方法。
[0089]
综上，本发明提供的一种图像识别方法、系统和存储介质，该方法基于四元数广义核稀疏主成分分析。首先基于图像的熵、红、绿、蓝四个分量信息进行四元数实表示，解决了图像像素熵信息丢失的问题。
[0090]
其次，根据四元数实表示矩阵将样本特征空间投影到高维空间，采用核函数的方法将线性特征转化为非线性特征，从而更容易区分所述类别不同但特征近似的图像样本，
另外，在非线性投影的过程中，使用的p范数欧式距离中的p是可调的任意非负值，体现了广义的特征，即在图像特征提取时能针对噪声、亮度、雾气等干扰因素灵活调节，使得能识别复杂多变的医疗图像；另外，p值的灵活可调，不仅可以防止训练过拟合，保证识别效率的稳定性，而且也解决了训练过程中手动调参得繁琐过程。
[0091]
再者，构造核函数的过程中权重的设置，将行列方向的最大投影散度联系在一起计算，体现了双边性，综合考虑了训练样本的所有方向特征，使得计算出的核稀疏主成分更加合理，后续的图像识别精度更加可靠准确；最后，本发明还采用了基于四元数保结构算法的交替方向乘子法，使得计算时间更短、内存占用少以及计算成本低。
[0092]
应当理解，虽然本说明书按照实施方式加以描述，但并非每个实施方式仅包含一个独立的技术方案，说明书的这种叙述方式仅仅是为清楚起见，本领域技术人员应当将说明书作为一个整体，各实施方式中的技术方案也可以经适当组合，形成本领域技术人员可以理解的其他实施方式。
[0093]
上文所列出的一系列的详细说明仅仅是针对本发明的可行性实施方式的具体说明，它们并非用以限制本发明的保护范围，凡未脱离本发明技艺精神所作的等效实施方式或变更均应包含在本发明的保护范围之内。