基于RCS序列阶跃效应的抛物面天线载荷指向估计方法与流程

基于rcs序列阶跃效应的抛物面天线载荷指向估计方法
技术领域
1.本发明属于航天雷达探测技术领域，具体涉及一种基于rcs序列阶跃效应的抛物面天线载荷指向估计方法。


背景技术：

2.随着空间技术的不断发展，空间已成为维护国家安全和打赢现代信息化战争的制高点，精准掌握航天器轨迹信息、运动状态、几何形状与物理参数等特征信息是在轨航天器工作状态参数获取的关键。雷达以全天候、全天时、快响应、高可靠的突出技术优势在空间目标监视系统中的地位和作用日益显现。
3.航天器载荷指向估计是描述航天器在轨工作状态的重要特征。目前，现有的卫星载荷指向估计大多是基于雷达isar成像进行识别。例如欧空局s.lemmens等人利用合作目标的3d仿真数据库与目标实测图像轮廓信息匹配搜索反演航天在轨姿态参数；西班牙gmv公司在目标isar图像特征匹配的基础上，实现了自动化的目标状态连续测量；zhou, y等人在文献“attitude estimation and geometry reconstruction of satellite targets based on isar image sequence interpretation. ieee transactions on aerospace and electronic systems,55(4), pp.1698-1711.”推导了目标三轴稳定情况下在轨姿态参数与目标典型矩形部件在isar成像平面投影的显示表达，并根据序列特性反演目标在轨姿态参数。
4.然而，对于携带抛物面天线载荷的航天器，由于其存在主动isar成像易散焦、序列特性不稳健的问题，因此难以利用现有的序列isar像实现该类航天器载荷指向等特征的稳健估计。


技术实现要素：

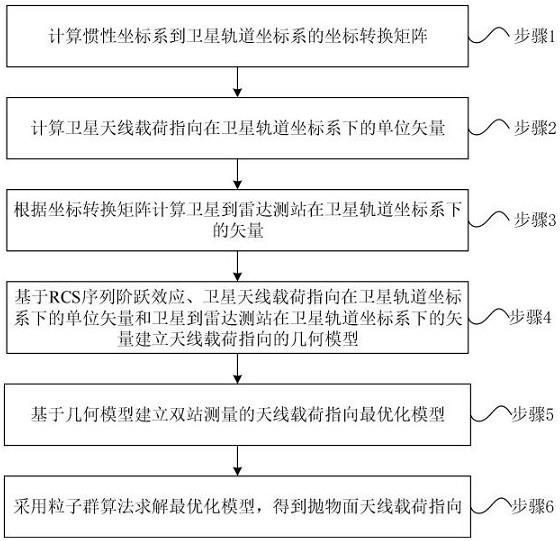
5.为了解决现有技术中存在的上述问题，本发明提供了一种基于rcs序列阶跃效应的抛物面天线载荷指向估计方法。本发明要解决的技术问题通过以下技术方案实现：一种基于rcs序列阶跃效应的抛物面天线载荷指向估计方法，包括：步骤1：计算惯性坐标系到卫星轨道坐标系的坐标转换矩阵；步骤2：计算卫星天线载荷指向在卫星轨道坐标系下的单位矢量；步骤3：根据所述坐标转换矩阵计算卫星到雷达测站在卫星轨道坐标系下的矢量；步骤4：基于rcs序列阶跃效应、所述卫星天线载荷指向在卫星轨道坐标系下的单位矢量和所述卫星到雷达测站在卫星轨道坐标系下的矢量建立天线载荷指向的几何模型；步骤5：针对所述几何模型，建立基于双站测量的天线载荷指向最优化模型；步骤6：采用粒子群算法求解所述最优化模型，得到抛物面天线载荷指向。
6.在本发明的一个实施例中，在步骤1中，所述惯性坐标系到卫星轨道坐标系的坐标转换矩阵表示为，其表达式为：；
其中，，，；为列向量，其表示卫星轨道坐标系下各坐标轴(x、y、z)的单位矢量，表示卫星质心在惯性坐标系下的位置参数，表示取模值。
7.在本发明的一个实施例中，在步骤2中，所述卫星天线载荷指向在卫星轨道坐标系下的单位矢量表示为，其表达式为：；其中，、分别表示卫星初始探测情况下天线载荷指向为对地方向、且为z轴时，天线载荷指向的滚动角和俯仰角。
8.在本发明的一个实施例中，步骤3包括：3a)对雷达测站在地心地固坐标系的位置矢量进行转换，得到惯性坐标系下雷达测站的位置矢量，其表达式为：；其中，为岁差矩阵，为章动矩阵，为地球旋转矩阵，为极移矩阵，表示转置，表示时刻；3b)根据计算卫星到雷达测站在惯性坐标系下的位置矢量，计算公式为：；其中，表示卫星质心在惯性坐标系下的位置矢量；3c)根据所述坐标转换矩阵和步骤3b)计算的计算卫星到雷达测站在卫星轨道坐标系下的矢量，计算公式为：；其中，表示惯性坐标系到卫星轨道坐标系的坐标转换矩阵。
9.在本发明的一个实施例中，步骤4包括：4a)计算t时刻卫星到雷达测站在卫星轨道坐标系下的矢量与卫星天线载荷指向在卫星轨道坐标系下的单位矢量的夹角，计算公式为：
；4b)利用雷达观测携带抛物面天线载荷航天器的rcs序列具有明显的阶跃效应，找出雷达测站的和时刻；其中，时刻为rcs序列阶跃效应开始的时刻，时刻为rcs序列阶跃效应结束的时刻；4c)根据在和时刻时，在卫星轨道坐标系下，卫星到雷达测站的矢量与卫星天线载荷指向的单位矢量夹角均为抛物面天线的圆锥角，构建天线载荷指向的几何模型如下：；其中，和分别表示和时刻卫星轨道坐标系下，卫星到雷达测站的矢量与卫星天线载荷指向的单位矢量夹角，表示抛物面天线的圆锥角。
10.在本发明的一个实施例中，步骤5包括：5a)利用双站测量信息建立最优化模型求解的目标函数，表示为：；其中，代表雷达测站1和雷达测站2；5b)建立基于rcs特征的约束条件为：。
11.在本发明的一个实施例中，步骤6包括：6a)将步骤5a )构建的目标函数作为为粒子群算法的适应度函数，并将步骤5b)中的约束条件作为粒子群算法的约束条件；6b)引入适应度惩罚函数，当粒子所在位置不满足约束条件时，其适应度函数值为无穷大；6c)定义变量寻解空间为：；6d)采用粒子群算法寻优求解，得到抛物面天线载荷指向。
12.本发明的有益效果：本发明利用雷达观测携带抛物面天线载荷航天器的rcs具有明显的阶跃效应，建立了卫星载荷指向估计的数学计算模型，实现了抛物面天线载荷的精确估计，克服了现有方法利用序列isar图像对于携带抛物面天线载荷的航天器存在主动成像易散焦、序列特性不稳健，难以实现该类航天器载荷指向等特征的稳健估计的问题，充分挖掘了抛物面天线
载荷指向窄带雷达特征信息，提高了雷达测量信息的利用率。
13.以下将结合附图及实施例对本发明做进一步详细说明。
附图说明
14.图1是本发明实施例提供的一种基于rcs序列阶跃效应的抛物面天线载荷指向估计方法的流程示意图；图2是本发明实施例提供的天线载荷指向示意图；图3是本发明实施例提供的抛物面天线rcs阶跃效应示意图；图4是本发明实施例提供的雷达探测抛物面天线航天器测量模型示意图；图5是本发明实施例提供的双站测量条件下探测角变化曲线图。
具体实施方式
15.下面结合具体实施例对本发明做进一步详细的描述，但本发明的实施方式不限于此。
16.实施例一雷达散射截面积(radarcross section，rcs)是特征测量雷达高稳健可靠的特性测量信息。由于基于雷达观测携带抛物面天线载荷航天器的rcs具有明显的阶跃效应，本实施例在此基础上结合航天器轨道参数、雷达测站位置实现了航天器抛物面天线载荷指向估计。
17.具体的，请参见图1，图1是本发明实施例提供的一种基于rcs序列阶跃效应的抛物面天线载荷指向估计方法的流程示意图，其包括：步骤1：计算惯性坐标系到卫星轨道坐标系的坐标转换矩阵。
18.1a)首先，基于卫星tle根数，通过轨道外推，得到卫星质心在惯性坐标系(j2000坐标系)下的位置参数；其中，分别表示时间、位置矢量和速度矢量。
19.1b)然后，利用上述参数计算卫星轨道坐标系的各坐标轴(、、)的单位矢量：（1）(2）（3）则惯性坐标系(j2000)到卫星轨道坐标系(xyz)的坐标转换矩阵可以表示为：（4）式中，为列向量。
20.步骤2：计算卫星天线载荷指向在卫星轨道坐标系下的单位矢量。
21.具体的，请参见图2，图2是本发明实施例提供的天线载荷指向示意图。卫星初始探测情况下天线载荷指向为z轴、对地方向，假设天线载荷指向的滚动角为，俯仰角为，绕旋转轴顺时针方向为正，则轨道坐标系下天线载荷指向单位矢量可以表示为：（5）步骤3：根据所述坐标转换矩阵计算卫星到雷达测站在卫星轨道坐标系下的矢量。
22.3a)对雷达测站在地心地固坐标系的位置矢量进行转换，得到惯性坐标系下雷达测站的位置矢量，其表达式为：（6）式中，为岁差矩阵，为章动矩阵，为地球旋转矩阵，为极移矩阵，表示转置，表示时刻。
23.3b)根据计算卫星到雷达测站在惯性坐标系下的位置矢量，计算公式为：（7）式中，可由步骤1a)获得。
24.3c) 根据所述坐标转换矩阵和步骤3b)计算的计算卫星到雷达测站在卫星轨道坐标系下的矢量，计算公式为：（8）为步骤1计算得到的坐标转换矩阵。
25.步骤4：基于rcs序列阶跃效应、所述卫星天线载荷指向在卫星轨道坐标系下的单位矢量和所述卫星到雷达测站在卫星轨道坐标系下的矢量建立天线载荷指向的几何模型。
26.4a)计算t时刻卫星到雷达测站在卫星轨道坐标系下的矢量与卫星天线载荷指向在卫星轨道坐标系下的单位矢量的夹角，计算公式为：（9）4b)利用雷达观测携带抛物面天线载荷航天器的rcs序列具有明显的阶跃效应，找出雷达测站的和时刻；其中，时刻为rcs序列阶跃效应开始的时刻，时刻为rcs序列阶
跃效应结束的时刻。
27.具体的，地基雷达观测携带抛物面天线载荷航天器时，当航天器抛物面天线载荷与雷达对视时雷达测量的窄带rcs具有明显的阶跃效应。请参见图3，图3是本发明实施例提供的抛物面天线rcs阶跃效应示意图。找出雷达测站的和时刻，也即rcs序列阶跃效应开始和结束的时刻。
28.4c)根据在和时刻时，在卫星轨道坐标系下，卫星到雷达测站的矢量与卫星天线载荷指向的单位矢量夹角均为抛物面天线的圆锥角，构建天线载荷指向的几何模型。
29.具体的，基于步骤4b)得到的和时刻，已知抛物面天线的圆锥角为，在时刻时，雷达探测波束刚好进入抛物面天线内部，在rcs序列特征曲线上表示为阶跃效应开始，此时在轨道坐标系下卫星到雷达位置的矢量与卫星天线指向夹角理论上为。同理，在时刻，雷达探测波束刚好离开抛物面天线内部，在rcs序列特征曲线上表示为阶跃效应结束，同样在轨道坐标系下卫星到雷达位置的矢量与卫星天线指向夹角理论上也为，如图3所示，建立载荷指向几何求解模型为：（10）需要说明的是，理论上可根据公式10进行方程联立求解得到天线载荷指向和，但考虑到雷达的测量信息误差以及解的不唯一性，本实施例提供了一种新的求解方法，其利用双站测量信息，建立最优化求解的目标函数和特征约束条件，然后利用粒子群算法进行求解。
30.步骤5：针对所述几何模型，建立基于双站测量的天线载荷指向最优化模型。
31.5a)利用双站测量信息建立最优化模型求解的目标函数，表示为：（11）其中，代表雷达测站1和雷达测站2。
32.5b)建立基于rcs特征的约束条件。
33.具体的，由于雷达波束从时刻进入抛物面天线内部和时刻离开抛物面天线内部，在到时刻之间完全处于抛物面天线内部，因此卫星到雷达位置的矢量在时刻与卫星天线指向夹角理论上都小于，建立基于rcs特征约束条件为：（12）步骤6：采用粒子群算法求解所述最优化模型，得到抛物面天线载荷指向。
34.6a)将步骤5a )构建的目标函数，也即式11作为为粒子群算法的适应度函数，并将
步骤5b)中的约束条件也即式12作为粒子群算法的约束条件；6b)引入适应度惩罚函数，当粒子所在位置不满足约束条件时，其适应度函数值为无穷大，表示为：（13）6c)定义变量寻解空间为：（14）6d)采用粒子群算法寻优求解，得到抛物面天线载荷指向。
35.本发明利用雷达观测携带抛物面天线载荷航天器的rcs具有明显的阶跃效应，建立了卫星载荷指向估计的数学计算模型，实现了抛物面天线载荷的精确估计，克服了现有方法利用序列isar图像对于携带抛物面天线载荷的航天器存在主动成像易散焦、序列特性不稳健，难以实现该类航天器载荷指向等特征的稳健估计的问题，充分挖掘了抛物面天线载荷指向窄带雷达特征信息，提高了雷达测量信息的利用率。
36.实施例二下面通过仿真试验，对本发明的有益效果进行验证说明。
37.1、试验条件本次仿真试验中各项参数的设置如下表1所示：表1 仿真参数设置
38.2、试验内容及结果分析2.1和时刻获取
假设卫星抛物面天线的圆锥角度，抛物面天线载荷指向角度为，通过计算得到轨道坐标系下卫星到雷达测站位置的矢量方向与卫星天线指向的夹角，将该角度定义为探测角，探测角随时间变化曲线如图5所示。
39.从图5中得出测站1的时刻为8时35分54秒，时刻为8时37分44秒，测站2的时刻为8时35分41秒，时刻为8时36分31秒。
40.2.2 粒子群求解。
41.通过对应的和时刻点，利用pso算法进行求解，将初始种群规模设置为30，迭代次数500次，通过多次仿真得到卫星载荷指向角度的一个最优解为。
42.2.3 结果分析从仿真结果可知，载荷指向估计值与实际设置值误差非常小，本方法具有较好的精度，验证了本发明的先进性。
43.以上内容是结合具体的优选实施方式对本发明所作的进一步详细说明，不能认定本发明的具体实施只局限于这些说明。对于本发明所属技术领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干简单推演或替换，都应当视为属于本发明的保护范围。