一种基于群智协同的阿基米德螺线移动模型及构建方法

本发明涉及移动模型，具体为一种基于群智协同的阿基米德螺线移动模型及构建方法。

背景技术：

1、移动模型(mobiltity model)采用数学方法抽象并描述现实应用场景下节点的运动情况，以尽可能准确地模拟现实场景下节点的运动特征。显然，节点的移动模型直接决定了网络的拓扑结构，进而也很大程度影响着网络的性能。此外，由于不同的移动模型往往适用于不同的应用场景，因此采用合适的移动模型对于研究高动态自组网的各种协议性能及其评估分析具有重要意义。尽管人们已经提出了多种移动模型，但它们大多适应于低速移动场景下，无法应用于高动态的应用场景。所以我们提出了一种基于群智协同的阿基米德螺线移动模型及构建方法，以便于解决上述中提出的问题。

技术实现思路

1、本发明的目的在于提供一种基于群智协同的阿基米德螺线移动模型及构建方法，以解决上述背景技术提出的多种移动模型无法应用于高动态的应用场景的问题。

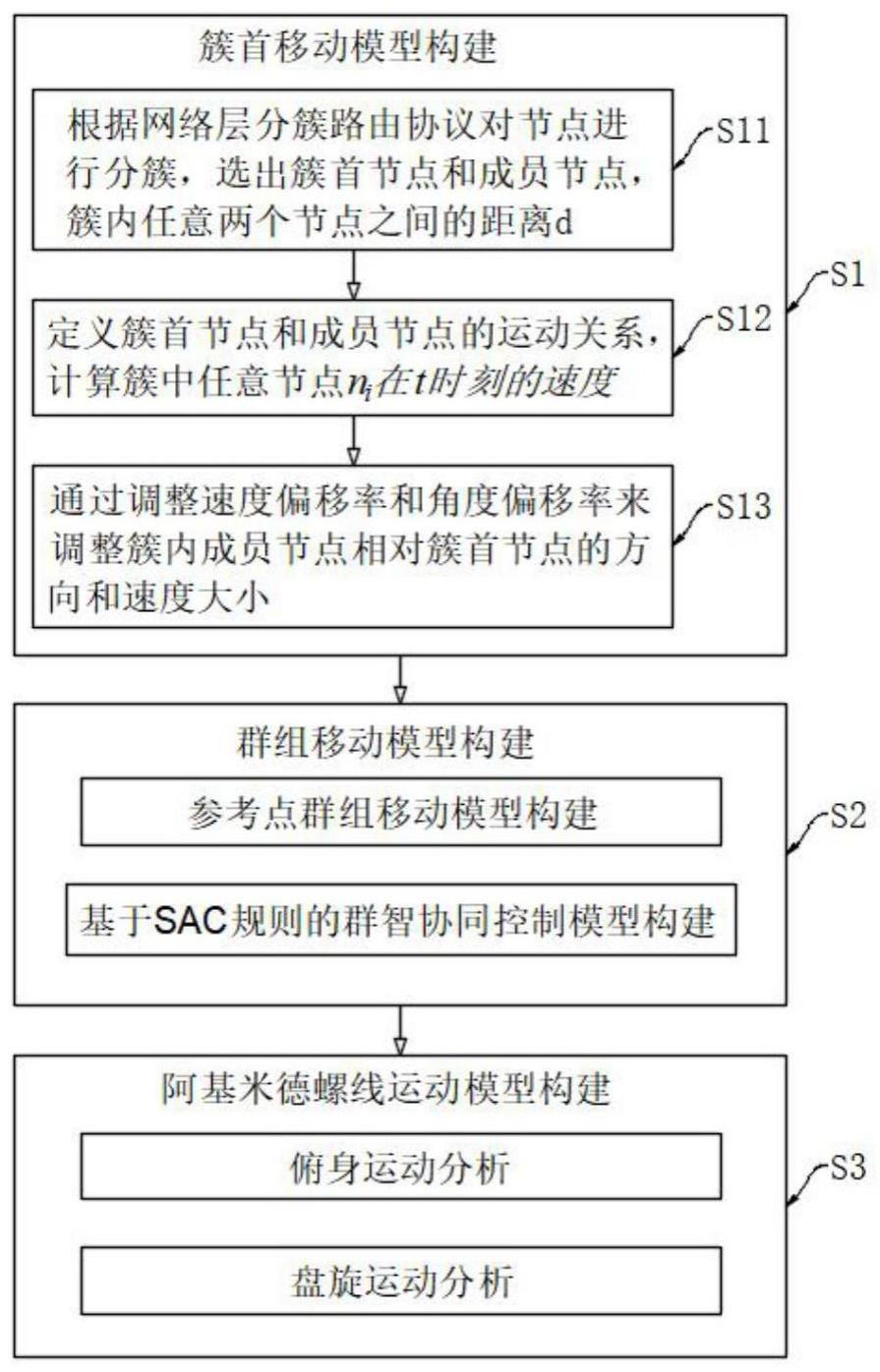
2、为实现上述目的，本发明提供如下技术方案：一种基于群智协同的阿基米德螺线移动模型构建方法，其特征在于：包括以下步骤:

3、s1：簇首移动模型构建

4、s2：群组移动模型构建

5、s3：阿基米德螺线运动模型构建

6、节点的运动由俯冲和盘旋两阶段构成：第一段是从akm s0(0,0,a)的高空点俯冲至bkm s1(0,0,b)处；第二段是做阿基米德螺线运动，其中簇首节点的速度初始为节点间的相对速度为100m/s，簇中节点的速度根据相应公式进行速度更新；

7、s31：俯冲运动

8、当节点在做俯冲运动时，会到空气阻力f(t)和重力g的影响，空气阻力大小计算公式如下：

9、

10、其中，c为空气阻力系数；ρ为空气密度；s物体迎风面积；为物体与空气的相对运动速度，根据参数所知参数c、s为定值，高度和空气密度的关系如下：

11、

12、则f(t)可写为：

13、

14、

15、故阻力和节点速度的平方成正比，节点的运动可分解为y轴和z轴方向，则y轴方向的空气阻力大小为：

16、

17、

18、z轴方向的空气阻力大小为：

19、

20、

21、由于在第一段俯冲运动时节点做自由落体运动，故当节点从s0(0,0,a)的高空点俯冲至s1(0,0,b)时，x轴的值恒为0；

22、s32：盘旋运动

23、当节点从s1(0,0,a)处开始做盘旋运动时，x轴会以阿基米德螺线的方式开始变化，故只对y轴和z轴进行分析；

24、z轴方向运动分析：

25、节点在z轴上只受到重力和空气阻力，取向下方向为正方向，则重力g为正，空气阻力为负，由牛顿第二定律可得：

26、

27、由于速度是路程s关于时间t的一阶导数，加速度是路程s关于时间t的二阶导数，故上式可写为：

28、

29、当节点做俯冲运动时，节点在z轴上的速度为0，即z`(0)＝0，z(0)＝0，将其带入公式(1-24)中可得到z轴上下落距离和时间的函数关系为：

30、

31、式中，m为节点质量，g为重力加速度，对其求导可得到下落速度和时间的函数变化关系：

32、

33、当重力g和空气竖直向上的空气阻力相等时，即

34、

35、此时，簇首节点将匀速下降；

36、y轴方向运动分析：

37、在y轴方向上，节点只受到空气阻力的影响，取节点运动的速度方向为正方向，由牛顿第二定律可得：

38、

39、由于速度是路程s关于时间t的一阶导数，加速度是路程s关于时间t的二阶导数，故上式可写为：

40、

41、而y轴方向上簇首节点的初始速度为300m/s，即y`(0)＝0，y(0)＝0，将其带入到公式(1-29)得到y轴上的距离和时间的函数关系为：

42、

43、对上式求导，可得y轴方向上的速度和时间函数变化关系：

44、

45、盘旋运动轨迹是阿基米德螺线，从高度akm处到高度ckm处，俯冲运动的终点s1(0,y1,a)变为螺线运动的起点，而s2(x1,y1,104m)为螺线运动的终点，而z轴方向上依旧只受到空气阻力和重力的影响，俯冲运动终点的速度vleader(t1)成为盘旋运动的初速度，故下落速度和时间的函数关系为：

46、

47、对其积分后得到距离和时间的关系为：

48、

49、

50、在做阿基米德螺线运动时，其平面坐标方程为：

51、yleader(t)＝a+(α+βωleader(t-t1))cos(ωleader(t-t1))  (1-35)

52、xleader(t)＝b+(α+βωleader(t-t1))sin(ωleader(t-t1))  (1-36)

53、式中，ωleader为恒定角速度，参数a、b、α决定了螺线的中心和起点位置，参数β决定曲线之间的距离，上式满足以下公式：

54、

55、式中，tend表示簇首节点做第二段运动结束的时间。

56、优选的，s1中簇首移动模型构建包括以下步骤：

57、s11：根据网络层分簇路由协议对节点进行分簇，选出簇首节点和成员节点，假设簇n内包含了三个节点n0、n1和n2，其中，n0节点为簇首节点，n1和n2节点为成员节点，簇中任意两个节点如n1和n2的空间坐标可表示为(x1,y1,z1)和(x2,y2,z2)，根据公式(1-1)可得簇内任意两个节点之间的距离d，公式(1-1)为：

58、

59、s12：定义簇首节点和成员节点的运动关系，假设簇内任意节点之间距离d的范围是：100m＜d＜500m；

60、簇中的任意节点ni在t时刻的速度根据公式(1-2)计算；

61、

62、是成员节点相对于簇首节点的一个随机偏移矢量，大小是介于[0，d]之间的一个随机数，d表示偏移距离，偏移距离100m<d<500m，偏移方向是介于[0，2π]之间的随机数；

63、s13：更新运动状态，节点运动状态更新包括两个方面：速度和角度；

64、速度更新公式为(1-3)，角度更新公式为(1-4)，

65、

66、θn1(t)＝θn0(t)+α.adr*m(α)  (1-4)

67、式中，α表示速度偏移率，β表示角度偏移率，m(s)是最大相对速度，值为100m/s，m(α)是最大偏转角度，其值为2π，通过调整速度偏移率和角度偏移率来调整簇内成员节点相对簇首节点的方向和速度大小。

68、优选的，s2中群组移动模型构建包括参考点群组移动模型构建和基于sac规则的群智协同控制模型构建。

69、优选的，参考点群组移动模型构建方法为：

70、在t时刻群组n内成员节点i的移动向量可表示为：

71、

72、式中，是群组n的移动向量，是群组n中的成员节点i偏移的随机运动向量，是一个随机均匀分布在参考点周围的向量，其大小在[0，r]区间取值，r是以参考点为圆心的圆半径，其方向在区间[0，2π]取值。

73、优选的，在高动态飞行器自组网中，当群组节点发射后，节点会分散并按照分簇协议进行分簇，在到达特定目标点之后进行聚合实现群组的智能协同控制，基于sac规则的群智协同控制模型构建方法为：

74、s21：在sac规则的基础上重新定义三种群组智能运动行为，并且为所定义的三种规则赋予簇首移动模型；

75、基于sac规则的三种智能运动行为分别定义为：分离、对齐和聚集；

76、根据节点间的排斥规则，使得节点相互之间排斥到安全距离之外，即两个节点之间距离必须大于100m，使节点在三维空间中呈现无碰撞的分布状况；故节点间的分离运动定义为：

77、

78、式中，为节点i排斥范围内节点的数量，表示节点i进入另一个节点的排斥范围时的方向，表示j节点的位置，表示i节点的位置，当节点i进入到以节点j为圆心，以100m为半径的圆中时，即触发排斥运动，节点i向着反方向运动；

79、当节点运动时，由于成员节点与簇首节点之间的平均运动方向有保持一致的趋势，且两节点之间距离d的根据实际应用场景定义为：100m＜d＜500m；故节点间的对齐运动定义为：

80、

81、

82、式中，是节点i的对齐方向，是节点i相邻节点的平均速度，是节点i的速度，nc是节点i周围邻居节点的数量。

83、当节点运动到特定位置执行任务时，为了提高执行任务的成功率，需要多个节点共同执行，故定义聚集运动行为是以群组中心为圆心，能够对成员节点进行吸引，故节点间的聚集运动定义为：

84、

85、

86、式中，表示节点聚集的方向，为群组的中心，n为节点总数。

87、s22：更新节点速度

88、使用向量表示节点i在t时刻的合速度，反映节点移动的速度和方向，其速度更新的规则定义为：

89、

90、式中，参数α、β和γ表示三种运动行为的权重，且α+β+γ＝1，当三种运动行为的权重取不同的值时，节点的运动状态不同。

91、s23：计算节点最终速度

92、通过对s221和s222中公式的整理，可得节点最终的移动速度为：

93、

94、s24：每个簇中有承担簇间通信的簇首节点，将该簇首节点在三种运动中进行建模；

95、在l*l*l的三维空间中，定义n个自治体中存在m(m<n)个簇首节点a(t)，簇首节点的感知半径为该簇中最长的半径rm，且rm>r，rm区域不重叠，簇首节点之间可以相互通信，簇首节点的集合公式为：

96、

97、式中，表示簇首节点的集合，

98、s25：为了表述节点间的一致性，定义一个个体归一的速度，即该速度越大时，表示节点的簇间同步性越高，效果就越好；

99、

100、式中，表示节点个体归一的速度。

101、与现有技术相比，本发明的有益效果是：

102、针对高动态飞行器移动的现实应用场景下，本发明提出了一种基于群智协同的阿基米德螺线移动模型(asmm-cic)。该模型利用群智协同的思想，借助于阿基米德螺线的理论，通过构建簇首移动模型，并与典型的生物群自组织boids模型的群智规则(sac)相结合，实现了一种新颖的且适合于高动态飞行器的移动模型。仿真实验表明，阿基米德螺线移动模型(asmm-cic)一方面较现有的移动模型表现出更优的动态性，另一方面在现有的路由协议中具有更好的通信性能。为了验证所提出的阿基米德螺线移动模型(asmm-cic)性能，本发明选取了经典的rpgm移动模型和粒子群模型(pso模型)作为比较对象，并从网络平均链路生存期、平均邻居节点率、平均路径变化率以及对路由协议性能影响四个角度进行了实验。实验结果表明，本发明所提出的阿基米德螺线移动模型(asmm-cic)在总体上较rpgm移动模型和粒子群模型具有更好的性能。