一种基于蚁群算法的配送路径优化方法与流程

本发明涉及路径优化算法领域，具体而言，涉及一种基于蚁群算法的配送路径优化方法。

背景技术：

1、目前的仓库电力物资的运输业务主要分为两种，一种是常规物资的配送，即常提及配送清单内的配送业务；另一种是急救包业务的配送。两项业务由不同的物流公司负责，有不同的收费方式，常规电力物资的配送收费模式比较简单，不按车辆行驶里程数计算，按次数计算，从一个仓库取一批货物，分别送到不同地点，算一次，有调度人员根据需要配送的物资随机安排。急救包业务的配送日期和送货地点位置是固定的，根据配送行驶的里程数收费，配送过程的路径随机，在规定时间内送达即可。

2、在运输送货环节，车辆的运输成本和人力成本在总成本中占据了较大比例，在满足终端用户需求的前提下，对运输环节进行高效益的管理有助于节省成本，同时提高运输效率。但是，目前对于仓库中的配送环节没有进行合理处理，各项配送业务的收费标准不一，运输物资时间不确定，从而造成了配送车辆装载率不高，车辆空间利用率低，车辆配送路径非最优的情况，使得不必要的运输成本增加。因此，可以通过科学的量化计算提高车辆装载率，减小车辆配送的里程数，从而实现配送环节的高效益。

3、目前的研究最主要、关键的技术问题是对安排配送的车辆没有提前对配送路径做具体合理的规划，配送路径选择不当，导致不必要的成本花费，同时在配送常规物资时对于车辆装载率没有做相关的评估，车辆的装载率低。因此，在基于各种成本条件的前提下，提出一种改进的蚁群算法建立配送路径优化模型，综合考虑载重量、运载车的长宽高、运载车辆数量和交通阻塞系数等因素求解上述问题，实现配送任务最多、使用车辆最少、提高配送速度，从而达到减少运力成本、提供运输效率的目标。

4、需要说明的是，上述背景技术部分公开的信息仅用于加强对本发明的背景的理解。

技术实现思路

1、本发明的目的在于提供一种基于蚁群算法的配送路径优化方法，进而实现完成配送任务最多、使用车辆最少、提高配送速度，从而达到减少运力成本、提供运输效率的目标。

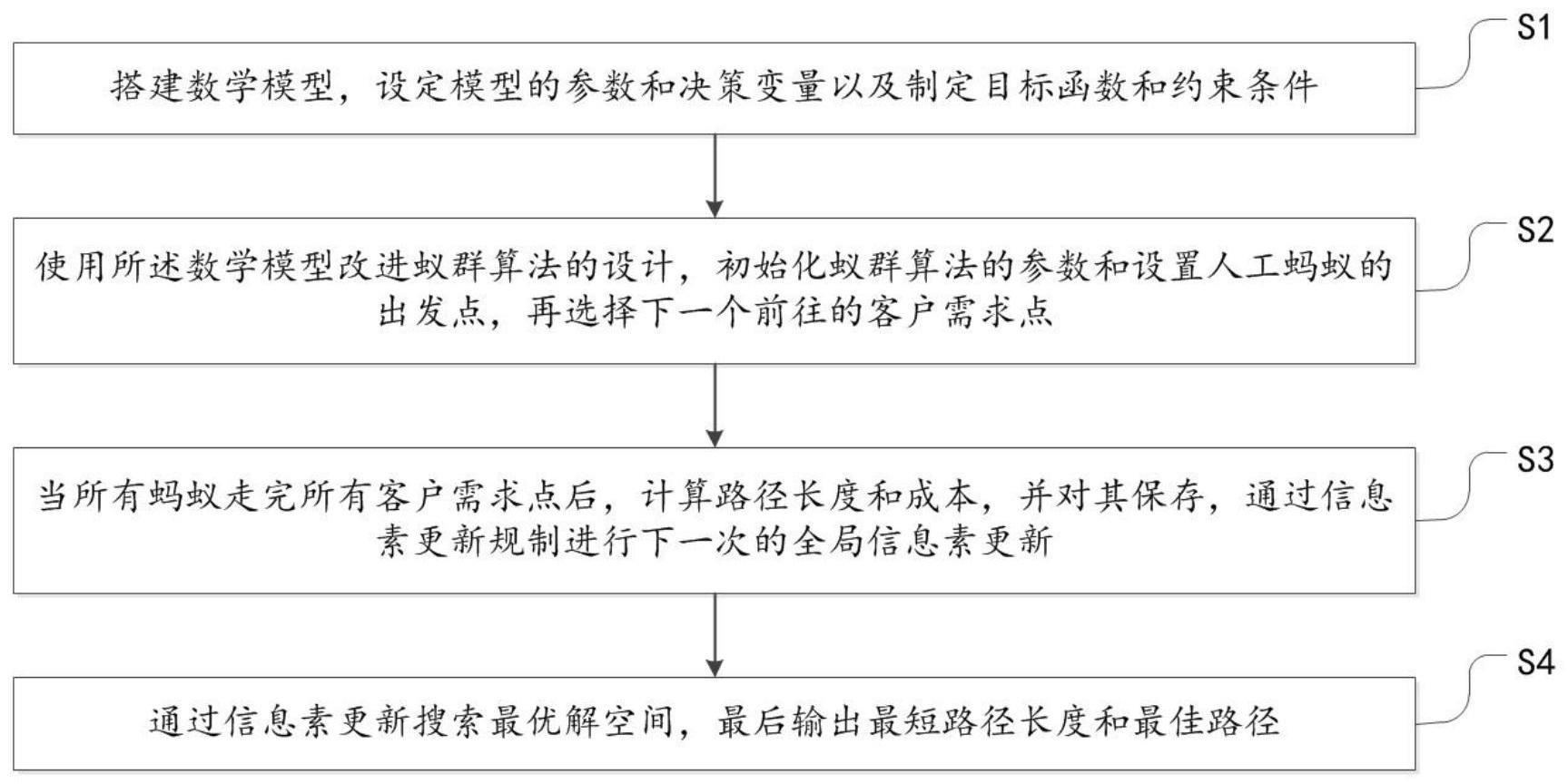
2、本发明技术解决方案为：一种基于蚁群算法的配送路径优化方法，包括：

3、搭建数学模型，设定模型的参数和决策变量以及制定目标函数和约束条件；

4、使用所述数学模型改进蚁群算法的设计，初始化蚁群算法的参数和设置人工蚂蚁的出发点，根据设计的转移概率再选择下一个前往的客户需求点；

5、当所有蚂蚁走完所有客户需求点后，计算路径长度和成本，并对其保存，通过信息素更新规制进行下一次的全局信息素更新；

6、通过信息素更新搜索最优解空间，最后输出最短路径长度和最佳路径。

7、基于前述方案，使用人工蚂蚁的行走路径行为模拟车辆对客户需求点配送的情况。

8、基于前述方案，上述搭建数学模型的方法，包括：

9、s11：假设模型，其中所述模型假设的内容包括但不限于：

10、有若干个仓库和需求点及地理位置信息、任意两点之间的路径距离已知；

11、仓库拥有的物资信息和车辆已知；

12、有多辆互相有差异且拥有唯一编号的运载车辆，其运载重量、货箱的长宽高均已知且能够满足运输任务的需求量；

13、每个订单配送信息，物资存放的仓库点与对应的需求点信息和需求物资的重量、长宽高已知；

14、每辆运载车辆的固定成本已知；

15、每辆车的行驶速度和最大工作时长已知。

16、s12：设定模型的参数和决策变量，其中所述模型参数和决策变量的内容包括但不限于：

17、p个仓库op、n个配送需求点op+n、每个需求点的需求物资gn种类有n种、每种物资需求量c1、c2、……cn、物资长度ln、物资宽度fn、物资高度hn、仓库i拥有的车辆数si、第p个仓库对应的第k辆运载车辆的承重能力第p个仓库对应的第k辆运载车辆货箱的长度宽度高度从oi到oj的运输距离dij、运载车辆的固定成本(包括人工成本、折旧成本、管理成本等)r1、从oi到oj的路径上由于环境天气等原因导致的交通阻塞系数wij，分别表示车辆k从点oi驶向点点oj，仓库p的物资由车辆k进行运输，需求点p的物资由车辆k进行运输，车辆k运输第n个需求点每种质量为cn的物资。

18、s13：制定目标函数，其中所述模型以里程数最小、总成本最低为目标函数：

19、

20、minz2＝r1+r2，

21、minz1代表里程数最小，minz2代表成本最低，r1为固定成本，r2为运输成本。

22、s14：制定约束条件，其中所述模型的约束条件包括：

23、条件a：

24、条件b：

25、

26、

27、条件c：

28、条件a表示每辆车的配送的总需求量不能超过其承载能力；条件b表示每辆车配送物资中每个设备长宽高不能超过运载车的长宽高限制；条件c表示从配送点出发与返回的车辆数要相等且不能超过其拥有的车辆数。

29、基于前述方案，上述模型目标函数总成本中固定成本与派遣的运载车辆数量成正比，运输成本与行驶里程数成正比。

30、固定成本函数表达式为：

31、

32、运输成本函数表达式为：

33、

34、基于前述方案，上述改进蚁群算法的设计的方法，包括但不限于：

35、初始化蚁群算法的参数，从0开始对客户需求点进行编号，记录客户需求点的总数customer_number；

36、设置车辆k的出发点为配送中心，其位置编号为0，所有车辆出发点为0；

37、车辆k在出发点出发后计算需求点之间的转移概率再使用轮盘赌的方式选择下一个前往的客户需求点。

38、基于前述方案，上述车辆k在出发点出发后引入交通阻塞系数计算需求点之间的转移概率，转移概率的计算公式为：

39、

40、集合allowedk为存储车辆k在到达客户需求点i之后还没到达的客户需求点；α为信息素重要程度因子，τij(t)为客户需求点ij之间的信息素含量；β为启发函数重要程度因子；启发函数为ηij(t)＝1/dij；wij(t)为交通阻塞系数,与一般计算不同在本次方案中加入交通阻塞系数wij，提高配送效率。交通阻塞系数的影响元素较多，比如环境天气、车辆类型等，其衡量标准也不一样。在本次方案中根据地图app实时查询在每两个客户需求点行驶所需的时间衡量，所需的时间越少交通拥堵系数越小。假设该车辆位于出发点，从出发点到其他客户需求点的时间已知，则两客户需求点之间的交通拥堵系数为从出发点到该点所用时间与出发点到其他客户需求点的时间之和的比值，交通拥堵系数矩阵的对角线元素均为0。交通拥堵系数越小被选择的概率应当越大。

41、基于前述方案，上述车辆k计算完转移概率后使用轮盘赌的方式选择下一个前往的客户需求点，在(0，1)之间产生一个随机数，选取大于该随机数且最接近该随机数的被选择概率对应的客户需求点，作为下一个前往的客户需求点。当没有满足的被选择概率时，则在未访问的客户需求点随机产生一个路径，作为下一个客户需求点，以此在保证有解的同时增大路径选择的随机性。

42、基于前述方案，上述信息素更新采用全局更新的蚁周模型求解信息素增量。

43、基于前述方案，上述信息素更新规制为：当所有蚂蚁都走完所有客户需求点后，形成m条路径，更新修改任意两点之间的信息素总量，两点之间信息素总量计算公式为：τij(t+1)＝(1-ρ)τij(t)+δτij，其中，(1-ρ)τij(t)为上次迭代剩余的信息，δτij为本次迭代增加的信息。

44、基于前述方案，上述任意两点之间的信息素的计算过程为任意两个客户需求点ij之间信息素的计算过程：第k只蚂蚁在第j个城市和第j+1个城市之间增加的信息素q/lk，所有蚂蚁在第j个城市和第j+1个城市之间增加的信息素之和得到本次迭代第j个城市和第j+1个城市之间增加的信息素，计算公式为：

45、

46、

47、q为信息素常数，表示蚂蚁循环一次所释放的信息素总量，lk为第k只蚂蚁本次迭代经过路径的总长度。

48、基于前述方案，上述改进蚁群算法的设计的具体步骤为：

49、s220：设定算法初始值；

50、s221：设置车辆k的出发点，钟村仓库为配送中心，位置编号为0，所有车辆的出发点都在位置0开始；进一步设置人工蚂蚁数量m，设置为客户需求点的1.5倍；每一次完整的迭代产生m个蚂蚁行走的完整路径，要求访问所有客户需求点；

51、s222：设定迭代次数iter_begin＝iter_begin+1，执行各步骤；

52、s223：根据转移概率公式计算m只蚂蚁的转移概率，当没有满足的被选择概率时，在未访问的客户需求点随机产生一个作为路径下一个客户需求点，车辆在送货过程中应满足约束条件；

53、s224：当m只蚂蚁访问了所有客户点，计算配送成本并对路径进行保存；

54、s225：更新信息素；

55、s226：对迭代次数进行判断，如果达到预先设置最大迭代次数iterations，则停止迭代，输出最优结果，否则转到步骤s33。

56、本发明的有益效果为：

57、一方面，本发明提出了基于改进蚁群算法的配送路径优化方法，针对目前研究中较少考虑交通状况对配送的影响，综合各种配送成本及车辆装载率、车辆空间利用率建立多目标化的模型，以降低运力成本、提供运输效率为目标设计改进蚁群算法，为电力物流的运输配送研究领域提供了相关理论依据。

58、另一方面，本发明在传统蚁群算法的节点选择过程中引入了交通阻塞系数对转移概率函数的计算公式进行了调整，在一定程度上更贴近车辆实际行驶的状况，提高了运输效率。

59、最后一方面，本发明在计算转移概率，没有满足的被选择概率时，在未访问的客户需求点随机产生一个作为路径下一个客户需求点，在保证有解的同时增大路径选择的随机性，进而实现配送环节的高效益。