一种基于特征学习的多标签分类模型训练方法及分类方法与流程

本发明涉及人工智能，尤其是一种基于特征学习的多标签分类模型训练方法及分类方法。

背景技术：

1、在使用深度学习模型进行训练时，首先要对大量的数据进行人工标注，实际场景下，单个实例往往存在多个标签，手动的标注多个标签比标注单个标签更为复杂，为了解决数据挖掘过程中的分类问题，多标签学习随着机器学习的发展开始兴起。

2、具体来说，多标签学习对数据分类时，首先使用训练集对分类模型进行训练学习，得到一个可以有效的对测试集数据预测标签的分类模型，最后利用分类模型对未标记的数据进行标记。

3、然而现有的分类模型在训练时，并未考虑到标签间正负相关性的问题，例如，在一副图像中，海洋与轮船大概率会同时出现(正相关)，而海洋与火车大概率不会同时出现(负相关)；此外，现有技术还没有考虑到，不同类的标签有其特有的特征，但相同的类标签之间又有其公共的共享数据特征，因此现有的分类模型的分类精度不高。

技术实现思路

1、针对现有技术的上述问题，本文的目的在于，提供一种基于特征学习的多标签分类模型训练方法及分类方法，以解决现有技术中没有考虑到，不同类的标签有其特有的特征，但相同的类标签之间又有其公共的共享数据特征，因此现有的分类模型的分类精度不高的问题。

2、为了解决上述技术问题，本文的具体技术方案如下：

3、一方面，本文提供一种基于特征学习的多标签分类模型训练方法，包括：

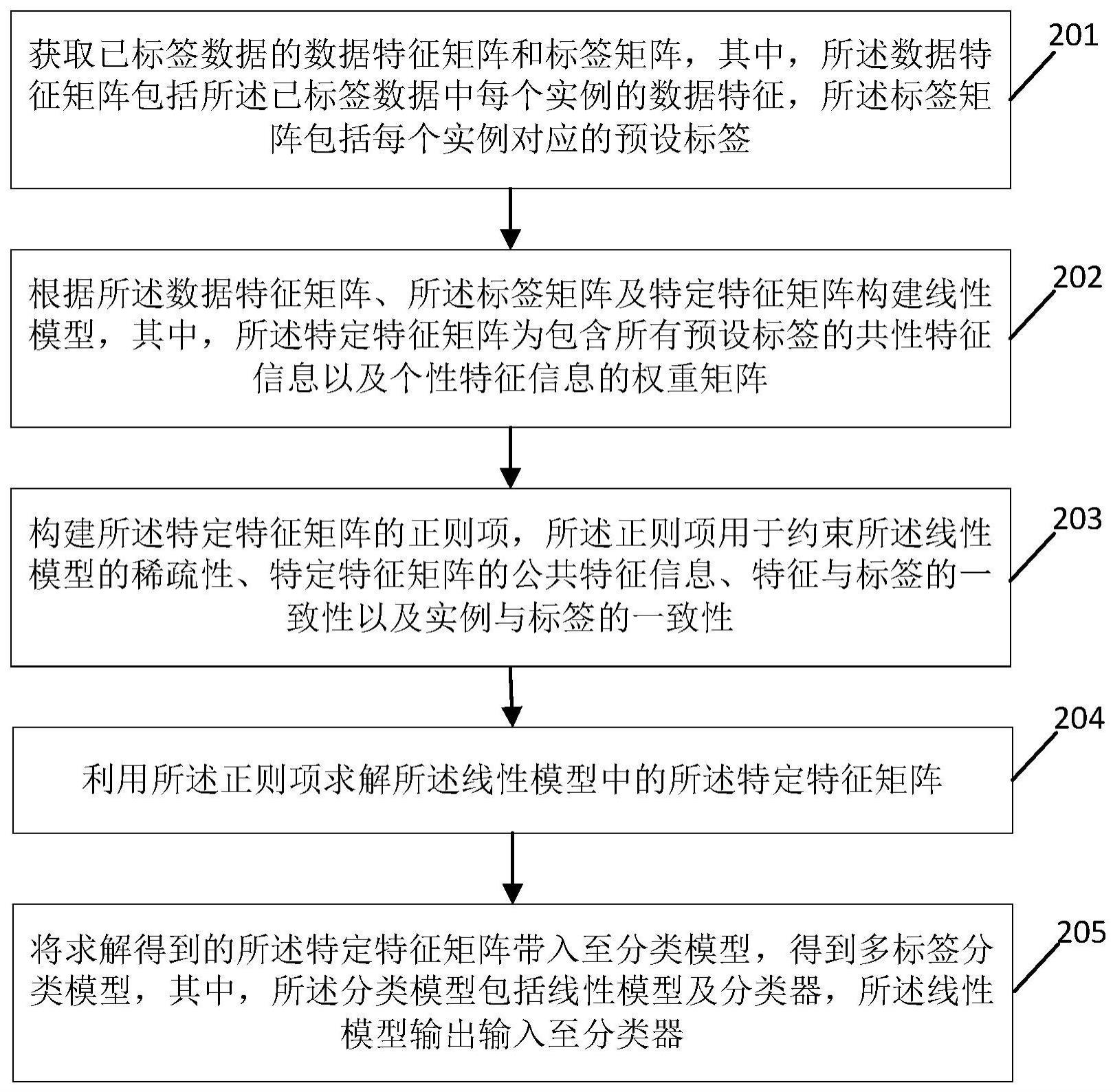
4、获取已标签数据的数据特征矩阵和标签矩阵，其中，所述数据特征矩阵包括所述已标签数据中每个实例的数据特征，所述标签矩阵包括每个实例对应的预设标签；

5、根据所述数据特征矩阵、所述标签矩阵及特定特征矩阵构建线性模型，其中，所述特定特征矩阵为包含所有预设标签的共性特征信息以及个性特征信息的权重矩阵；

6、构建所述特定特征矩阵的正则项，所述正则项用于约束所述线性模型的稀疏性、特定特征矩阵的公共特征信息、特征与标签的一致性以及实例与标签的一致性；

7、利用所述正则项求解所述线性模型中的所述特定特征矩阵；

8、将求解得到的所述特定特征矩阵带入至分类模型，得到多标签分类模型，其中，所述分类模型包括线性模型及分类器，所述线性模型输出输入至分类器。

9、作为本文的一个实施例，所述构建特定特征矩阵的正则项，进一步包括：

10、利用特定特征矩阵的一范数及二一范数，构建用于约束所述线性模型的稀疏性和所述特定特征矩阵的公共特征信息的第一正则项；

11、利用k最近邻的方式确定每个实例的最近邻实例，根据各实例的最近邻实例确定相邻实例的相似性公式，由相似性公式构成约束所述实例与标签一致性的第二正则项；

12、利用k最近邻的方式以及最大后验概率确定所述标签矩阵对应的正负相关性矩阵，根据所述正负相关性矩阵确定所述标签矩阵中任两个标签间的正负相关特定特征，由所述正负相关特定特征构成约束所述特征与标签的一致性第三正则项。

13、作为本文的一个实施例，所述线性模型表示为：

14、

15、其中，w为特定特征矩阵，x为所述数据特征矩阵，y为所述标签矩阵，x为n×d维的矩阵，w为d×c维的矩阵，y为n×c维的矩阵，n为实例数量，d为特征数量，c为标签数量。

16、作为本文的一个实施例，所述第一正则项利用如下公式表示：

17、λ3‖w‖1+λ5‖w‖2,1

18、其中，λ3，λ5为模型的超参数，‖w‖1为所述特定特征矩阵的一范数，用于约束线性模型的稀疏性；‖w‖2,1为所述特定特征矩阵的二一范数，用于提取特定特征矩阵的公共特征信息。

19、作为本文的一个实施例，所述第二正则项利用如下公式表示：

20、

21、其中，sij为利用k最近邻的方式确定每个实例的最近邻实例，xi＝[xi1,xi2,…,xin]表示第i个实例的特征向量，xj＝[xj1,xj2,…,xjn]表示第j个实例的特征向量，n表示实例的个数，x＝{xi1，…,xin}，y＝{y1，…,yc}，其中n为实例个数，c为标签数量，tr为矩阵的迹，ls为特定特征矩阵的拉普拉斯变换，f为(xw)t的简化形式。

22、作为本文的一个实施例，所述利用k最邻近的方式以及最大后验概率确定标签矩阵对应的正负相关性矩阵，进一步包括：

23、使用k邻近算法和最大后验概率计算所述正相关矩阵和负相关矩阵：

24、

25、

26、

27、

28、其中，pij为正相关矩阵，pij中的n(xi)是在实例xi中，yl是1的情况下yj也是1的概率，nij中的n(xi)为负相关矩阵，表示在实例xi中，yl是0的情况下yj是1的概率；xi＝[xi1,xi2,…,xin]表示第i个实例的特征向量，yi＝[yi1,yi2,…,yic]表示第i个实例中可能存在的标签集合，n表示实例的个数，c表示标签的数量，yij＝{1,0}c表示如果实例中包含标签yi，则yi＝1；如果实例中不包含标签yi则yi＝0。

29、作为本文的一个实施例，所述第三正则项包括正相关特定特征和负相关特定特征；

30、所述正相关特定特征利用如下公式表示：

31、

32、其中，pij是正相关矩阵，wi为第i个实例对应的特定特征矩阵，wj为第j个实例对应的特定特征矩阵，w为待训练的特定特征矩阵，wt为待训练的特定特征矩阵对应的转置矩阵，lp为所述正相关矩阵对应的拉普拉斯矩阵，dp为lp中每一个元素加p确定得到，p为正相关矩阵中的一个元素，<wi,wj>

33、为特定特征矩阵中的第i个特征与第j个特征，根据具有共享数据特征的两个实例间相似特征最小构建；

34、所述负相关特定特征利用如下公式表示：

35、

36、其中，nij是负相关矩阵，wi为第i个实例对应的特定特征矩阵，wj为第j个实例对应的特定特征矩阵，w为待训练的特定特征矩阵，wt为待训练的特定特征矩阵对应的转置矩阵，ln为所述负相关矩阵对应的拉普拉斯矩阵，dn为ln中每一个元素加p确定得到，p为正相关矩阵中的一个元素，根据具有共享数据特征的两个实例间相似特征最小构建。

37、作为本文的一个实施例，所述利用所述正则项求解所述线性模型中的特定特征矩阵，进一步包括：

38、根据所述正则项及所述特定特征矩阵确定目标函数；

39、将所述数据特征矩阵和所述标签矩阵，导入至所述目标函数中进行迭代计算，得到满足优化条件的所述特定特征矩阵。

40、作为本文的一个实施例，所述目标函数利用如下公式表示：

41、

42、其中，λ1，λ2，λ3，λ4和λ5是模型的超参数，x为所述数据特征矩阵，y为所述标签矩阵，其中n为实例个数，c为标签数量，w为特定特征矩阵，‖w‖1为所述特定特征矩阵的一范数，用于约束线性模型的稀疏性；‖w‖2,1为所述特定特征矩阵的二一范数，用于提取特定特征矩阵的公共特征信息，ls为特定特征矩阵的拉普拉斯变换，lp为特定特征矩阵的正相关变换，ln为特定特征矩阵的负相关变换，f是(xw)t的简化形式。

43、另一方面，本文还提供一种多标签分类方法，包括：

44、将未标签数据的数据特征矩阵导入至任一项所述方法训练得到的多标签分类模型，得到所述未标签数据对应的特定特征矩阵；

45、将所述数据特征矩阵与所述特定特征矩阵相乘后带入所述多标签分类模型中的软阈值算子，得到数值矩阵；

46、将所述数值矩阵所有的元素均与所述多标签分类模型中的校准值相减，得到所述未标签数据对应的预测标签。

47、另一方面，本文还提供一种计算机设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现任意一项所述的多标签分类模型训练方法。

48、另一方面，本文还提供一种计算机可读存储介质，所述计算机可读存储介质存储有计算机程序，所述计算机程序被处理器执行时实现任意一项所述的多标签分类模型训练方法。

49、采用上述技术方案，通过获取已标签数据的数据特征矩阵和标签矩阵，其中，所述数据特征矩阵包括所述已标签数据中每个实例的数据特征，所述标签矩阵包括每个实例对应的预设标签，可以实现获取已标签数据中各项数据的特征以及对应的预设标签，并将其进行矩阵化，进而方便后续的计算；通过根据所述数据特征矩阵、所述标签矩阵及特定特征矩阵构建线性模型，其中，所述特定特征矩阵为包含所有预设标签的共性特征信息以及个性特征信息的权重矩阵，可以实现构建数据特征矩阵和标签矩阵之间对应的线性模型，即将所述数据特征矩阵和特定特征矩阵带入至线性模型后，可以得到标签矩阵；通过构建所述特定特征矩阵的正则项，所述正则项用于约束所述线性模型的稀疏性、特定特征矩阵的公共特征信息、特征与标签的一致性以及实例与标签的一致性，以及利用所述正则项求解所述线性模型中的所述特定特征矩阵，可以进一步约束线性模型，并求解得到特定特征矩阵，令最终的预测结果更加准确；通过将求解得到的所述特定特征矩阵带入至分类模型，得到多标签分类模型，其中，所述分类模型包括线性模型及分类器，所述线性模型输出输入至分类器，可以得到预测未标签数据中，每个数据标签的分类模型。

50、为让本文的上述和其他目的、特征和优点能更明显易懂，下文特举较佳实施例，并配合所附图式，作详细说明如下。