基于序列分解与子序列注意力机制的长时序预测方法和系统

本发明涉及时间序列分析，具体地，涉及一种基于序列分解与子序列注意力机制的长时序预测方法和系统。

背景技术：

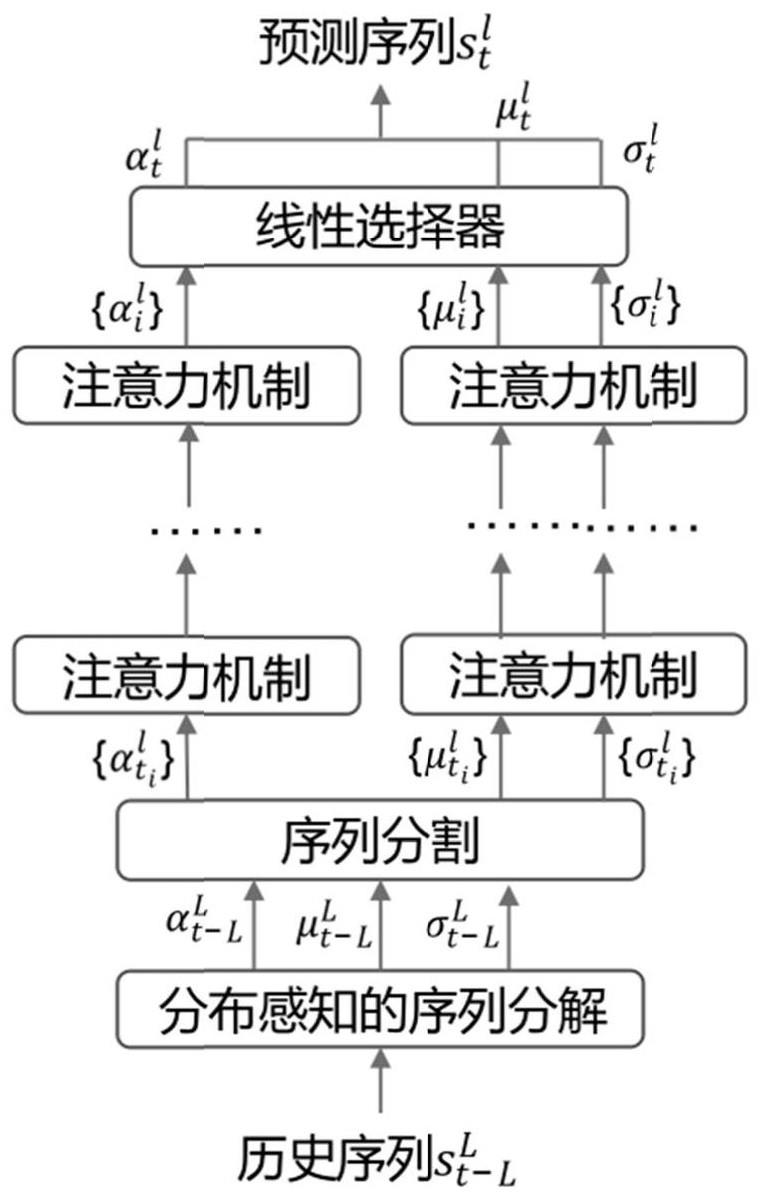
1、长期以来，时间序列分析与预测一直被广泛应用于各个领域，并发挥着举足轻重的作用，包括天气预报、交通量流量预测、金融市场分析等。近年来，为了更好预判未来较长一段时间内的变化规律，长时间序列预测任务逐渐成为了研究热点。与短时预测任务不同的是，长时序预测需要一次性输出未来较长一段时间内的变化情况，因此其模型更加关注于全方位提取序列中长期存在的依赖关系，例如周期特征等，而非仅仅关注于短期的趋势特征。

2、大多数长时间序列的预测均是通过迭代短时预测结果来实现。具体来说，首先通过模型得到较短未来的预测结果，而后以该预测结果作为模型的输入再进行下一时间段的预测，依次迭代下去，最后得到较长未来的预测序列。由于模型的预测结果相比于真实情况必然存在误差，因此通过迭代的方式进行预测必然会使得每一步的误差不断累积，最后的预测结果与真实值偏离地越来越大，因此并不适用于对长序列预测精度的要求。

3、当下，随着深度学习技术的发展，一些基于transformer结构的模型，通过直接一次性输出完整的长序列而非迭代的方式，大幅度提高了时间序列预测的精度，例如informer、autoformer、fedformer等。专利文献cn113935513a(申请号：cn202111003754.9)公开了一种基于ceemdan的短期电力负荷预测方法，包括，利用ceemdan对原始电负荷序列进行分解，获得若干imf分量及趋势分量；计算若干imf分量及趋势分量的样本熵值，并根据样本熵值对所述若干imf分量、趋势分量进行叠加形成新子序列；结合新子序列和特征注意力机制，构建lstm预测模型；利用lstm预测模型对新子序列进行预测，而后将各新子序列的预测结果进行叠加组合获得总的预测输出。以上研究更多关注于寻找长序列中各个时间点之间的依赖关系，由于模型规模较大、训练数据分布不稳定且噪声较大，因此容易出现严重的过拟合现象，极大地影响了长序列的预测精度。

技术实现思路

1、针对现有技术中的缺陷，本发明的目的是提供一种基于序列分解与子序列注意力机制的长时序预测方法和系统。

2、根据本发明提供的基于序列分解与子序列注意力机制的长时序预测方法，包括：

3、步骤1：通过滑动窗口的方式遍历原始序列，并分为等长度的三个成分序列，分别为：将求解过去多个时间点序列的均值作为当前时刻的趋势项成分，将求解的标准差作为尺度项成分，将原始序列按照均值和标准差标准化后的值作为平稳项成分；

4、步骤2：基于注意力机制，计算任意两个子序列之间发生随机事件的概率，得到每个子序列对未来的预测结果；

5、步骤3：通过一个线性筛选机制将所有预测结果加权并合成，得到最终预测结果。

6、优选的，所述步骤1包括：

7、同时感知序列的期望和标准差的变化，将二者的变化统一作为趋势项分离出原始序列中，使序列最终保留分布平稳的成分，具体策略为：给定时间序列s＝{x1,x2,…,xl,}，l为时间序列s的长度，设定其在长度为h的时间跨度内分布不发生变化，因此通过滤波得到三种成分：

8、趋势项μt满足：

9、

10、尺度项σt满足：

11、

12、最终剩余的平稳项则为：

13、

14、其中，t为三个成分序列的长度；i为索引号。

15、优选的，所述步骤2包括：

16、对于平稳成分，设定子序列之间独立同分布，并关注于序列间的独立性是否满足，具体为：首先定义两个子序列和之间的相关系数，表达式为：

17、

18、其中，表示子序列的第k个元素；由于平稳项已经将每个元素的期望标准化为0，即因此求相关系数简化为求余弦相似度，表达式为：

19、

20、随后依据相关系数ρij，定义随机事件eij为：

21、eij:ρ>|ρij|

22、其中，ρ为对相关系数随机采样得到的值，若两个子序列强相关，则必然|ρij|较大，因此事件eij的概率较小，即表明两个子序列和之间有很大置信度存在潜在的依赖关系；j为索引号。

23、优选的，对于非平稳成分，更关注序列之间的同分布特性，即关注于各个子序列的趋势变化特征，故定义两子序列之间的关系为：

24、

25、

26、两个子序列的趋势越相似，则δμ和δσ的值越小，则表明两个子序列之间存在趋势相关关系，故构造事件eij为：

27、eij:δμ<δμij

28、eij:δσ<δσij

29、当构造事件eij后，计算该事件的概率，基于蒙特卡罗采样的思想，直接使用样本中的ρij、δμij和δσij的分布作为其真实分布，因此事件eij的概率被统一定义为：

30、

31、其中，表示ρij、δμij和δσij；当表示ρij时，r为升序排名位次，当表示δμij和δσij时，r为样本中该值降序排名位次；n为排名总位次。

32、优选的，所述步骤3包括：

33、通过信息量定义各依赖关系的权重：

34、wij＝-logp(eij)

35、对于子序列其通过与其他序列的波动特征加权的方式生成预测结果

36、

37、其中，函数f用于提取子序列的波动特征。

38、根据本发明提供的基于序列分解与子序列注意力机制的长时序预测系统，包括：

39、模块m1：通过滑动窗口的方式遍历原始序列，并分为等长度的三个成分序列，分别为：将求解过去多个时间点序列的均值作为当前时刻的趋势项成分，将求解的标准差作为尺度项成分，将原始序列按照均值和标准差标准化后的值作为平稳项成分；

40、模块m2：基于注意力机制，计算任意两个子序列之间发生随机事件的概率，得到每个子序列对未来的预测结果；

41、模块m3：通过一个线性筛选机制将所有预测结果加权并合成，得到最终预测结果。

42、优选的，所述模块m1包括：

43、同时感知序列的期望和标准差的变化，将二者的变化统一作为趋势项分离出原始序列中，使序列最终保留分布平稳的成分，具体策略为：给定时间序列s＝{x1,x2,…,x1,}，l为时间序列s的长度，设定其在长度为h的时间跨度内分布不发生变化，因此通过滤波得到三种成分：

44、趋势项μt满足：

45、

46、尺度项σt满足：

47、

48、最终剩余的平稳项则为：

49、

50、其中，t为三个成分序列的长度；i为索引号。

51、优选的，所述模块m2包括：

52、对于平稳成分，设定子序列之间独立同分布，并关注于序列间的独立性是否满足，具体为：首先定义两个子序列和之间的相关系数，表达式为：

53、

54、其中，表示子序列的第k个元素；由于平稳项已经将每个元素的期望标准化为0，即因此求相关系数简化为求余弦相似度，表达式为：

55、

56、随后依据相关系数ρij，定义随机事件eij为：

57、eij:ρ>|ρij|

58、其中，ρ为对相关系数随机采样得到的值，若两个子序列强相关，则必然|ρij|较大，因此事件eij的概率较小，即表明两个子序列和之间有很大置信度存在潜在的依赖关系；j为索引号。

59、优选的，对于非平稳成分，更关注序列之间的同分布特性，即关注于各个子序列的趋势变化特征，故定义两子序列之间的关系为：

60、

61、

62、两个子序列的趋势越相似，则δμ和δσ的值越小，则表明两个子序列之间存在趋势相关关系，故构造事件eij为：

63、eij:δμ<δμij

64、eij:δσ<δσij

65、当构造事件eij后，计算该事件的概率，基于蒙特卡罗采样的思想，直接使用样本中的ρij、δμij和δσij的分布作为其真实分布，因此事件eij的概率被统一定义为：

66、

67、其中，表示ρij、δμij和δσij；当表示ρij时，r为升序排名位次，当表示δμij和δσij时，r为样本中该值降序排名位次；n为排名总位次。

68、优选的，所述模块m3包括：

69、通过信息量定义各依赖关系的权重：

70、wij＝-logp(eij)

71、对于子序列其通过与其他序列的波动特征加权的方式生成预测结果

72、

73、其中，函数f用于提取子序列的波动特征。

74、与现有技术相比，本发明具有如下的有益效果：

75、本发明提出了分布感知的序列分解算法和面向子序列的注意力机制，大幅度提高长时间序列预测任务的精度和效率，相比于其他模型，序列分解算法能够分离出平稳成分，使得模型具有更好的泛化能力，有效降低了过拟合现象；面向子序列的注意力机制将研究重点从单个时间点转向子序列，使得模型能够批量处理并分析更加整体与宏观的序列依赖关系，将注意力机制的时间复杂度从o(n2)降低至o(1)，大幅度减小长序列预测任务的模型规模并提高其效率；同时本发明基于显著性检验的思想优化了注意力机制的运算过程，使得其能够更有针对性地寻找子序列间的依赖关系，提高模型的预测精度和可解释性。