纤维增强复合材料截顶圆锥壳固有特性的分析方法

本发明涉及纤维增强复合结构，具体为纤维增强复合材料截顶圆锥壳固有特性的分析方法。

背景技术：

1、纤维增强复合材料由于其具有比模量、比强度高，质量轻，加工工艺性好等诸多优点，由其加工的复合梁、板、壳等结构被广泛应用于汽车化工、航空航天等高科技工业领域中。由于使用结构越来越复杂，工作环境越来越恶劣，因此引起的一系列振动问题(如结构的振动超标，振动疲劳破坏等)也越发严重。因此对于薄壁复合结构振动特性的研究，也越来越受到研究学者们的广泛关注。

2、固有特性的研究包括固有频率和模态振型两个部分，他们是振动特性研究的基础。目前，壳结构的广泛工程应用，引起了国内外研究人员对该结构进行深入研究的极大兴趣，并发展了许多研究其固有特性的方法，并取得了阶段性的成果。其中，张德众基于经典层合理论，利用半有限元分析的方法，对于叠层复合薄壳进行了自由振动的分析。tong基于donnell型方程，求解了拉弯耦合的复合锥壳的固有特性。朱显明等基于donnell壳体理论及幂指数求解的方法，通过在金属圆柱壳模型中引入半锥角的方法，求解了金属圆锥壳的振动特性。liang s基于四阶龙格-库塔法推导理论方程，从理论上探讨了利用传递矩阵法结合振动理论进行分析壳体固有特性的可行性。tripathi v等基于高阶剪切变形理论，求解了不同层压方案和厚径比下简支复合圆锥壳线性自由振动响应及固有特性，并通过文献及独立的蒙特卡罗模拟加以验证。quy等基于一阶剪切变形理论，采用改进的变分原理和多段划分技术推导了具有不同几何参数和材料参数的层合圆柱壳、圆锥壳和球壳的自由振动方程，并求解了固有特性。viola e等基于二维高阶剪切变形理论及微分求积法，对中厚层双曲壳的二维自由振动进行求解，并获得其固有特性。瞿叶高等基于傅里叶级数以及chebyshev多项式对层合壳的位移表达式进行多项式的展开，通过半解析区域分解的方法对复合圆柱壳的自由振动进行求解与分析。xiang x基于一阶剪切变形理论以及haar小波离散化方法，对复合圆锥壳，圆柱壳和环形板结构固有特性进行求解。su z基于一阶剪切变形理论，推导了功能梯度圆锥壳、圆柱壳和环形板的幂级数方程，并求解了相应结构的固有特性。dey s等采用概率有限元的方法，对纤维圆锥壳在纤维取向角和材料特性随机变化下的固有频率进行了统计分析。宋旭圆基于rayleigh-ritz法，对复合薄壁圆柱壳的固有特性进行求解。周正学等利用能量法，求解了纤维增强圆柱壳的固有特性，并进行了实验验证。hong zhang等基于简化板理论(spt)和二维改进的fourier-ritz方法，进行了环扇型板、圆扇形板、环形板的理论建模，并对结构的振动特性进行了分析。safarpour m等基于弹性理论，利用微分求积法和状态空间技术，提出了一种求解功能梯度圆柱壳、圆锥壳和圆环板振动特性的半解析方法。sobhani e等通过一阶剪切变形理论和哈密尔顿原理，利用等效计算的方法对碳纳米管表层与石墨烯芯层的三明治结构的固有特性进行了分析。niuy等通过一阶剪切变形理论(fsdt)结合chebyshev-ritz方法，研究了石墨烯板(gpl)增强复合材料锥形板和圆柱板在横向激励下的线性和非线性振动，并求解了固有特性。田宏业等基于一阶剪切变形理论构建了理论分析模型，并以不同类型弹簧模拟圆锥板结构的边界和连续性条件，分析了功能梯度锥型板的自由振动特性。夏鑫基于viogt-reuss原理和传递矩阵法对硬涂层阻尼薄壁截锥壳的固有特性进行研究，并通过有限元和文献比较的方法进行了验证。

3、从所掌握的文献研究内容可发现，目前对于壳类结构固有特性的研究，主要集中在各向同性材料以及功能梯度三明治所制成的圆柱壳上，而对于各向异性的纤维增强截顶圆锥壳结构固有特性的研究内容相对较少，且大都没有进行实验研究。纤维增强截顶圆锥壳所用材料存在各向异性的特点，同时由于半锥角的存在，使得其本构关系更加复杂，这使得准确预测其固有特性更加的困难。

技术实现思路

1、本发明提出了纤维增强复合材料截顶圆锥壳固有特性的分析方法，该方法具有原理清晰、适用性广、计算速度快等优点，可为工程实践中相应结构的固有特性预测提供指导和参考。

2、本发明提供纤维增强复合材料截顶圆锥壳固有特性的分析方法，包括以下步骤：

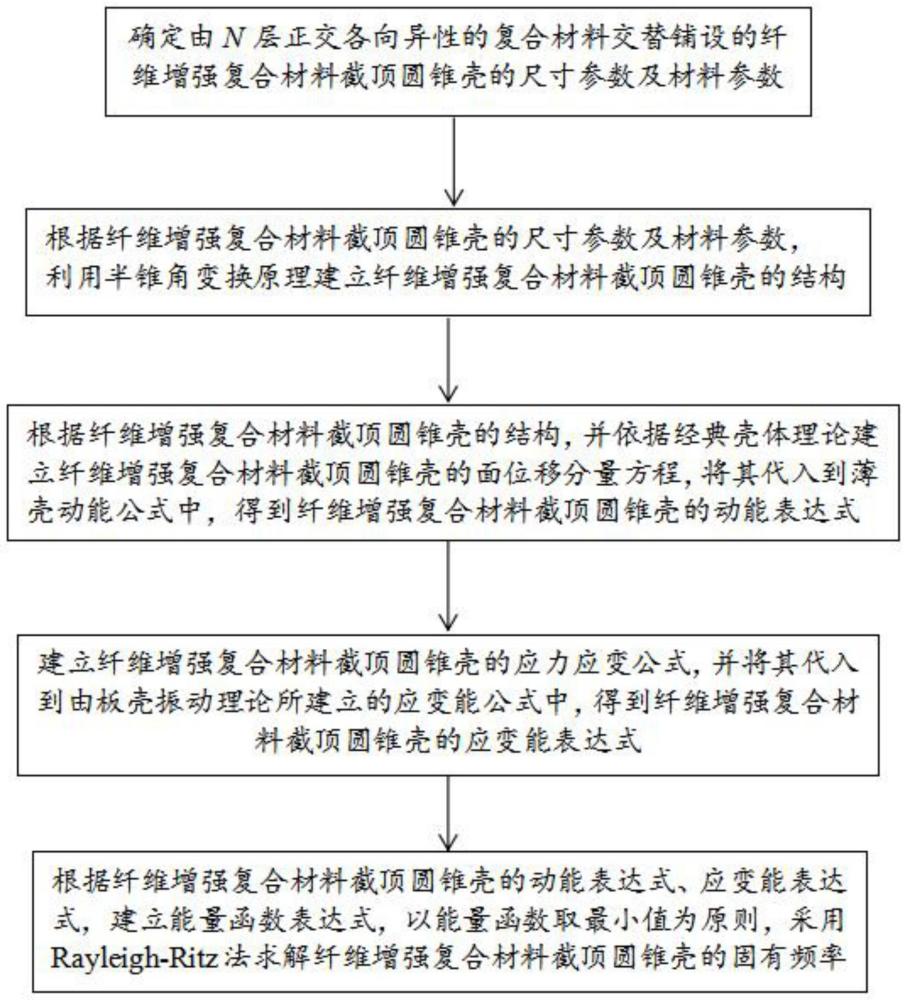
3、确定由n层正交各向异性的复合材料交替铺设的纤维增强复合材料截顶圆锥壳的尺寸参数及材料参数；

4、根据纤维增强复合材料截顶圆锥壳的尺寸参数及材料参数，利用半锥角变换原理建立纤维增强复合材料截顶圆锥壳的结构；

5、根据纤维增强复合材料截顶圆锥壳的结构，并依据经典壳体理论建立纤维增强复合材料截顶圆锥壳的面位移分量方程，将其代入到薄壳动能公式中，得到纤维增强复合材料截顶圆锥壳的动能表达式；

6、建立纤维增强复合材料截顶圆锥壳的应力应变公式，并将其代入到由板壳振动理论所建立的应变能公式中，得到纤维增强复合材料截顶圆锥壳的应变能表达式；

7、根据纤维增强复合材料截顶圆锥壳的动能表达式、应变能表达式，建立能量函数表达式，以能量函数取最小值为原则，采用rayleigh-ritz法求解纤维增强复合材料截顶圆锥壳的固有频率。

8、进一步地，依据经典壳体理论所建立的所述纤维增强复合材料截顶圆锥壳的面位移分量方程，如下：

9、

10、其中，u、v、w分别代表截顶圆锥壳任意一点的位移；

11、n为截顶圆锥壳的周向波数，ω为复合材料截顶圆锥壳的固有频率；

12、u为x方向上的振型函数；v为θ方向的振型函数；

13、w为z方向上的振型函数。

14、进一步地，所建立的所述纤维增强复合材料截顶圆锥壳的应力应变公式，包括：

15、对于正交各向异性材料，其应力应变的关系为：

16、

17、其中，γ12为12方向上的应变；ε1为1方向上的应变；ε2为2方向上的应变；σx为x方向上的应变；σy为y方向上的应变；σxy为xy面内的应变；

18、为材料常数，i＝1,2,6，j＝1,2,6；

19、其中，q11的表达式为q12的表达式为

20、q22的表达式为q66的表达式为q66＝g12；g12为面内剪切模量；

21、其中，μ1、μ2分别为不同方向的泊松比，且

22、当材料与主轴方向有一定的夹角时，第k层平面的应力应变关系在其夹角β下的关系为：

23、

24、其中，为引入半锥角系数的材料常数，i＝1,2,6，j＝1,2,6；

25、其中的表达式分别为：

26、

27、其中，βk为纤维铺层夹角；

28、根据love壳体理论，以及圆柱壳的半锥角变换原理，得到应力应变公式：

29、其中，εx为x方向的正应变，εθ为θ为圆周方向的正应变，γxθ为面应变，kx为x方向的曲率，kθ为θ圆周方向的曲率，kxθ为面扭转曲率，其表达式分别为：

30、

31、

32、

33、

34、

35、

36、其中，α为截顶圆锥壳半锥角。

37、进一步地，所述薄壳动能公式为：

38、

39、由板壳振动理论所建立的所述应变能公式为：

40、

41、其中，{ε}为应变向量，其表达式为：

42、{ε}＝{εx,εθ,εxθ,kx,kθ,kxθ} (13)

43、其中，s为薄膜刚度矩阵，对于复合材料截顶圆锥壳结构，其定义如下：

44、

45、其中，aij、bij、dij分别为刚度系数，其中，i＝1,2,6，j＝1,2,6，其表达式分别为：

46、

47、其中，hk、hk+1为复合材料截顶圆锥壳上下参考表面距。

48、进一步地，所述采用rayleigh-ritz法求解纤维增强复合材料截顶圆锥壳的固有频率，包括以下步骤：

49、建立截顶圆锥壳的中面位移方程，如下：

50、

51、其中，am、bm、cm为系数；

52、ψu、ψv、ψw为是满足边界条件与力学边界条件正交函数；

53、nt为通过ritz方法的截断系数；

54、r为圆锥等效半径，其表达式为

55、其中，r1为截顶圆锥壳小径端，r2为截顶圆锥壳大径端；

56、对边界条件多项式进行正交化处理，从而获得一系列正交多项式为：

57、

58、其中，k>2；

59、φ(ξ)为正交多项式中的权函数，其表达式为：

60、φ(ξ)＝ξp(1-ξ)q  (18)

61、其中，p、q分别代表r＝r1、r＝r2处边界状态参数，p、q取值在自由、简支和固定时分别取0,1,2。

62、当取时，系数函数bk和ck表达式为：

63、

64、

65、其中能量函数表达式l为：

66、l＝tmax-umax  (21)

67、其中，tmax为最大动能；umax为最大应变能；

68、在求解截顶圆锥壳固有频率时，要求解使所有的能量函数l求解最小值的待定参数：

69、

70、将公式(16)、(17)带入到公式(18)后，再求解下式(20)中的特征值，式(20)如下：

71、(k-ω2m)q＝0  (23)

72、其中，k和m分别为截顶圆锥壳的刚度矩阵和质量矩阵；

73、其中，特征向量为q＝(am,bm,cm)t；

74、令系数行列式为零，即：

75、det(k-ω2m)＝0  (24)

76、通过求解公式(20)的特征值，得到截顶圆锥壳的固有频率值。

77、与现有技术相比，本发明的有益效果：

78、本发明以纤维增强复合材料截顶圆锥壳为研究对象，以理论与实践相结合的方式分析了纤维增强截顶圆锥壳的固有特性。针对纤维增强复合圆锥壳的结构特性引入半锥角系数，考虑复合结构各向异性的影响，基于经典层合理论对其进行了理论建模；利用rayleigh-ritz法和正交多项式法求解了结构的固有特性。通过搭建相应的实验系统，以tc300/环氧树脂复合圆锥壳为研究对象进行测试，结果表明，本发明提出计算方法所获得固有频率的结果与试验测试结果间的误差在1.4％～2.3％之间，进而验证了所提出模型的正确性。最后，讨论了半锥角大小、不同约束方式和不同纤维铺层角度等参数对结构固有特性的影响规律。本发明所提出的该方法具有原理清晰、适用性广、计算速度快等优点，可为工程实践中相应结构的固有特性预测提供指导和参考。