一种用于精神分裂症病历图像特征选择的稀疏双向Spark方法

本发明涉及医学信息智能诊断，尤其涉及一种用于精神分裂症病历图像特征选择的稀疏双向spark方法。

背景技术：

1、脑疾病的识别是医学图像分析中的一个热点问题，脑图像的识别对脑疾病的预测有重要影响。随着静息态磁共振成像技术的发展，许多研究者开始关注脑区之间的功能连通性。大量研究发现，许多精神疾病都与患者大脑的功能连接有关。这些联系提供了潜在的生物标记物用于脑科疾病的临床诊断。精神分裂症是一种常见的精神疾病。通过对脑功能网络矩阵的信息进行处理，可以获得预测精神分裂症的生物学信息，从而提高精神分裂症的预测性能。特征选择是一种有效的预处理方法，它去除了对分类没有帮助的特征，提高了分类的泛化能力。

2、目前，没有任何可靠的诊断技术可以用来诊断精神疾病，而精神分裂症的高发率已经成为世界卫生关注的焦点。由于患者数量和需要处理的数据量庞大，迫切需要一个新的方法来有效的从众多数据中提取有助于精神分裂症预测的大脑区域，通过特征选择可以有效的帮助医生分析精神分裂症高风险患者，为医学图像分析的改进提供了一个新的方向。

技术实现思路

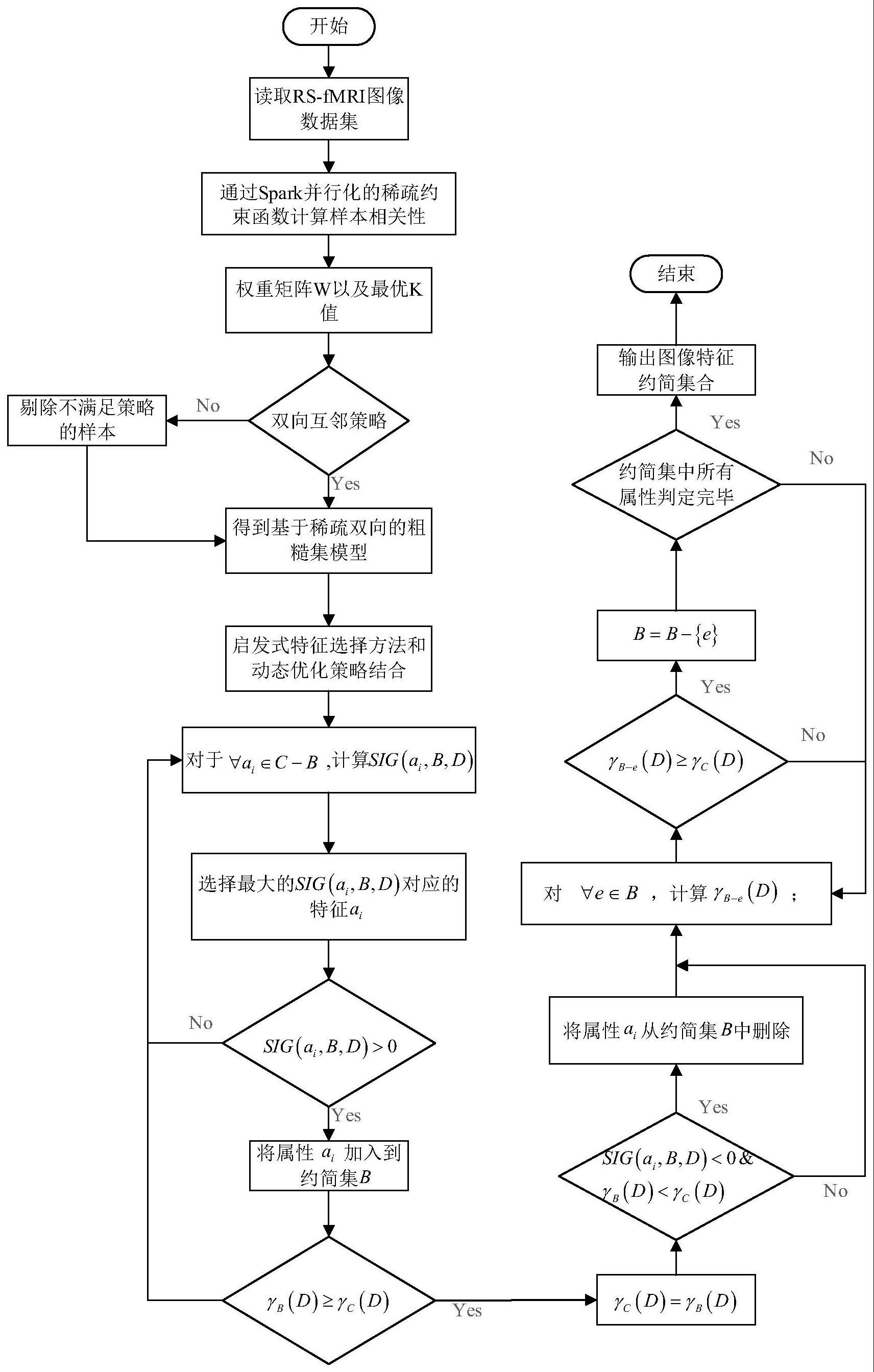
1、针对传统的基于近邻算法来处理不平衡数据，无法处理不同分布的数据，单向粒度的构建方法会导致部分噪声数据和离群点的被归入到粒度模型中，增加粒度的不确定性的技术问题，而提出了一种用于精神分裂症病历图像特征选择的稀疏双向k近邻spark方法；首先，基于稀疏约束函数得到每个样本的最优k值；其次，在粒度化过程中采用双向互邻策略。第三，动态优化策略是应用于提高特征选择算法的性能。最后，利用所提出的特征选择方法对大脑区域进行选择，提高了预测性能。

2、本发明的发明思想为：首先，在主节点上，读取大规模精神分裂症病历图像数据，对其进行预处理和划分，并将数据子集广播到相应的子节点上。在子节点上，通过spark并行化的稀疏约束模型刻画样本之间的联系，得到样本最优的k个邻居(k为邻居个数)。然后，在粒化过程中引入双向互邻策略，构造基于稀疏双向的spark粗糙集模型。在子节点上，将启发式特征选择方法和动态优化策略结合，选取预测精神分裂症的重要脑区域。本发明的有益效果为：该方法解决了数据集中样本分布不一致的问题，有助于精神分裂症的预测，为医学图像分析的改进提供了一个新的方向。

3、本发明是通过如下措施实现的：一种用于精神分裂症病历图像特征选择的稀疏双向spark方法，包括以下步骤：

4、s1：在主节点master上，读取大规模静息态功能磁共振成像(简称rs-fmri)的精神分裂症病历图像数据集，将分布不平衡的rs-fmri数据存储到数据库的分布式文件中，并进行数据预处理和划分操作。rs-fmri图像经过数据预处理后，使用解剖自动标记模板将其划分为若干个大脑区域。在大脑网络中，每个大脑区域代表一个独立的节点，分别提取每个节点的平均体素时间序列，将每个区域相似度较高的聚类到一起，计算每个区域的聚类系数，将系数转为一组一维特征向量，用这些系数来表示大脑网络的拓扑结构，建立脑区之间的脑功能连接网络，定义节点时间序列矩阵。

5、将精神分裂症病历图像转换为一个四元组决策信息系统s＝(u,c∪d,v,f)，其中u＝{x1,x2,……,xn}表示数据集中精神分裂症病历图像的患者对象集合，m表示精神分裂症病历的患者个数，xm表示第m个样本；c＝{a1,a2,…,an}表示精神分裂症病理属性的非空有限集合，n表示精神分裂症病理属性的个数，an表示第n个属性；d＝{d1,d2，……,dn}表示精神分裂症病历决策类别的非空有限集合，n表示精神分裂症病历决策类别的个数,dn表示第n个决策类别，且v＝∪a∈c∪dva，va是数据集属性a下数据对象所有可能的数据取值，f:u×c∪d→v表示一个信息函数，它为每个精神分裂症病历图像赋予一个信息值，即x∈u，f(x,a)∈va；

6、s2：在spark框架中，建立主控节点master和子节点slavei之间的通信。读取精神分裂症病历的数据集，将数据集s合划分成m个精神分裂症数据子集{s1,s2,……,sm}，其中sm表示第m个数据子集，且满足数据子集之和等于数据集，满足任意数据子集的交集为空，并将其广播到相应的子节点上。在子节点slaveri上，使用留一法列出病历图像样本xi，xi表示第i个精神分裂症病历图像样本。通过spark并行化的稀疏约束模型计算图像样本xi和其他样本(x1,x2,……,xi-1,xi+1,……,xj)之间的相关性，xj表示第j个数据集，其中j＜n。当行内尽可能多的元素为0时，约束才可能取得最小，即使得矩阵出现尽可能多的全零行，得到权重矩阵w，元素大小反应样本紧密程度，通过非零元素个数得到样本最优的k个邻居，获得k值，构造基于spark并行化的稀疏k近邻粒度模型。利用所有样本最优的k个邻居，生成关系矩阵，表示每个样本之间的距离关系；

7、s3：在子节点slavei中引入双向互邻策略，通过病历图像样本x和样本y的互邻信息重叠区域来判断，当样本x和样本y都属于对方的最近邻粒度，则样本y被选为样本x的最近邻,得到基于稀疏双向的spark粗糙集模型。令b表示精神分裂症病理特征非空有限集合的子集，则稀疏双向最近邻定义如下：

8、smkb(xi)＝{kb(xi)|xi∈kb(xj)∩xj∈kb(xi)}   (12)

9、其中，x关于特征子集b的最优邻居为xi表示精神分裂症病历图像数据子集中第i个样本，xj表示精神分裂症病历图像数据子集中第j个样本，kb(xj)表示样本xj在特征子集b下的k个邻居，kb(xi)表示样本xi在特征子集b下的k个邻居；

10、s4：将启发式特征选择方法和动态优化策略结合，在子节点slavei上，基于粒度的模型采用条件熵来评估模型的不确定性，在属性c-b子集中寻找具有最大属性重要度sig(ai,b,d)对应的属性，其中ai表示第i个属性，将其加入到属性集b中，若属性ai冗余则继续计算下一个具有最大属性重要度的属性。比较依赖性γb(d)和γc(d)，将属性集b中的冗余属性删除，γb(d)表示属性子集b对于决策类d的依赖度，γc(d)表示条件属性c对于决策类d的依赖度。利用依赖关系来评估近似的区域，得到各个子节点计算出的病理属性约简子集集合{r1,r2,……,rm},其中m表示子节点的个数，rm表示第m个子节点求出的属性子集。根据基于稀疏双向的spark并行模型对数据进行特征选择，由此选取预测精神分裂症的重要脑区域；

11、作为本发明提供的一种用于精神分裂症病历图像特征选择的稀疏双向spark方法进一步优化方案，所述步骤s3的具体步骤如下：

12、步骤s3.1：在子节点slaveri上，使用留一法列出样本xi，增加一个l1正则化，通过spark并行化的稀疏约束模型计算图像样本xi和其他样本(x1,x2,……,xi-1,xi+1,……,xj)之间的相关性，稀疏约束函数如下：

13、

14、其中是frobenius范数的平方，f是范数的选取方式，t是矩阵的转置变换，||·||1是1范数，rho是1范数的调优参数，取值在0到1之间，w为数据集的重构权重矩阵，xt表示数据集的转置矩阵；

15、步骤s3.2：在稀疏约束函数中利用1范数生成行稀疏性，当行内尽可能多的元素为0(甚至为全零行)时，约束才可能取得最小，即使得矩阵出现尽可能多的全零行。通过目标函数不断调节参数，获得重构权重矩阵w，通过矩阵的对应列获取样本xi的重构向量p。利用重构向量p中元素的大小反映样本紧密程度，其中非零元素的个数即为该图像样本的最优k值，构造基于spark并行化的稀疏k近邻粒度模型；

16、步骤s3.3：在子节点slaveri上，在基于spark并行化的稀疏k近邻粒度模型中加入互信息策略，通过样本x和样本y的互邻信息的重叠区域来判断，当样本x和样本y都属于对方的近邻粒度，则样本y被选为样本x的最近邻,得到基于稀疏双向k近邻的spark模型。

17、对于样本x和样本y满足

18、x∈kx(y)∩y∈ky(x)   (14)则样本y包含在样本x的稀疏双向的spark并行特征选择模型中，选择模型中符合该策略的样本，构造基于稀疏双向的spark粗糙集模型；

19、步骤s3.4：根据稀疏约束函数得到的最优k值和双向互邻策略，设计了构造基于稀疏双向的spark粗糙集模型。给定信息系统s,特征子集b中xi的稀疏双向邻居smkb(xi)，其上近似以及下近似分别定义为

20、

21、

22、步骤s3.5：计算d关于b的正域、负域和边界域分别定义为

23、

24、

25、

26、作为本发明提供的一种用于精神分裂症病历图像特征选择的稀疏双向spark方法进一步优化方案，所述步骤s4的具体步骤如下：

27、步骤s4.1：将启发式特征选择方法和动态优化策略结合，基于粒度的模型采用条件熵来评估模型的不确定性,在所述子节点slavei中，初始化属性集b，设计算属性重要度sig(ai,b,d)，并选择最大的属性重要度和对应的特征ai，属性集b关于决策属性d的条件邻域熵计算公式如下所示：

28、

29、属性重要度的计算公式如下所示：

30、sig(a,b,d)＝ceb(d)-ceb∪{a}(d)   (21)

31、其中ceb∪{a}(d)表示属性集b加入属性a后关于决策属性d的条件邻域熵。如果sig(ai,b,d)>0，则将对应的特征ai加入到选定的属性集b中，b＝b∪{ai}；

32、步骤s4.2：在所述从节点slavei中，根据限定约简的定义，计算更新后特征子集b对决策特征d的依赖度γb(d)，判断如果计算结果满足γb(d)≥γc(d)，则将γb(d)赋值给γc(d)，继续计算下一个特征ai，特征ai相对于特征子集b的依赖性可以描述为:

33、γb(d)＝|mkposb(d)|/|u|   (22)

34、步骤s4.3：在所述子节点slavei中，判断如果满足γb(d)≤γc(d)且sig(ai,b,d)＜0，则说明特征ai冗余，需将属性集b中的特征ai去除，b＝b-{ai}。直到将所有的属性都比较一遍；

35、步骤s4.4：若属性集b中的特征a不止一个且γb(d)≥γc(d)，则需验证其中是否有特征冗余。令计算γb-e(d)，如果γb-e(d)≥γc(d)，则将属性集b中的特征e去除；构建候选属性集合，并将其属性依次添加到属性约简集合red中。最后，在主节点master将子节点slavei所得的属性约简子集取交集得到属性约简集为r，特征选择算法进行单元化，获得所选脑区域。

36、与现有技术相比，本发明的有益效果为：

37、1、由于数据量大且算法需要遍历多次才能得到最优结果，会消耗大量时间、效率低，而采用分布式并行算法可提高计算效率。每个样本的最优的k个邻居通过相关样本的数量得到，其中样本之间的相关性通过spark并行化的稀疏约束模型学习。基于每个样本最优k值构造spark并行化的稀疏k近邻粒度。粒度模型的大小可以通过相关样本的体积来准确表征。利用范数产生行稀疏性，消除噪声数据的干扰。

38、2、由于数据空间中样本分布存在差异，传统k近邻统一的k值不能很好的进行粒度刻画，分类精度严重依赖邻居个数k的取值，基于双向互邻策略对稀疏互k最近邻信息粒进行处理。双向互邻策略考虑了数据分布的差异，提高了该粒子的性能。

39、3、通过针对非单调问题的动态优化策略，改进了经典启发式特征选择方法。该模型的特征显著性函数随特征的增加而非单调。当特征显著性测度不单调时，经典的启发式特征选择可能无效，特征选择算法的性能不断提高，避免了非单调性带来的性能下降。