一种物理模型驱动人工智能的磁共振波谱定量方法

本发明涉及磁共振波谱定量方法，尤其是涉及一种物理模型驱动人工智能的磁共振波谱定量方法。

背景技术：

1、γ-氨基丁酸(γ-aminobutyric acid，gaba)是各种精神和神经疾病的关键生物标志物，如双相情感障碍症、抑郁症、癫痫等。从磁共振波谱(magnetic resonancespectroscopy，mrs)中量化gaba是一个非常具有挑战性的任务，gaba的谱峰与其他代谢物的谱峰严重重叠(edden ra,barker pb,”spatial effects in the detection of gamma-aminobutyric acid:improved sensitivity at high fields using inner volumesaturation,"magnetic resonance in medicine,58(6):1276-82,2007.)。在gaba在3.0ppm的谱峰与肌酸(cr)和磷酸肌酸(pcr)引起的信号重叠；在2.3ppm处与谷氨酰胺和谷氨酸(glx)重叠；在1.9ppm处与n-乙酰天冬氨酸(naa)和n-乙酰天门冬氨酰谷氨酸(naag)发生重叠(craven ar,bhattacharyya pk,clarke wt,etal.,"comparison of sevenmodelling algorithms for gamma-aminobutyric acid-edited proton magneticresonance spectroscopy,"nmr in biomedicine,35(7):e4702,2022.)。最常用的定量gaba的mrs方法，是利用谱编辑方法生成的编辑谱序列帮助量化分析gaba。比如，j调制差分技术(rothman dl,petroff o,behar kl,et al.,"localized1h nmr measurements ofgamma-aminobutyric acid in human brain in vivo,"proceedings of the nationalacademy of sciences,90(12):5662-5666,1993)，生成谱编辑序列mega-press，从重新聚焦的edit-on频谱中减去非重新聚焦的edit-off频谱得到只保留那些受编辑脉冲影响的峰值的编辑谱(mullins pg,mcgonigle dj,o'gorman rl,et al.,"current practice inthe use of mega-press spectroscopy for the detection of gaba,"neuroimage,86:43-52,2014)。对于gaba来说，通常使用编辑谱在3ppm处的谱峰进行量化。但是通常预期的gaba的“伪双峰”在实现中很难观察到，原因是：(1)gaba在体内浓度很低，gaba的谱峰与其他代谢物的谱峰严重重叠；如肌酸(cr)和n-乙酰天冬氨酸(naa)，难以分离；(2)低浓度分子的信号与噪声几乎无法区分；(3)生理运动、b0场漂移，软件处理等问题可能会导致diff谱出现伪影，影响目标代谢物的量化分析。

2、现有的磁共振波谱量化分析方法主要包括基于峰值拟合和基于基集拟合的算法。基于基集拟合的方法lcmodel(vanhamme l,van den boogaart a,van huffel s,"improved method for accurate and efficient quantification of mrs data withuse of prior knowledge,"journal of magnetic resonance,129(1):35-43,1997.)被广泛认为是量化磁共振波谱的金标准，将磁共振信号建模为代谢物基集的线性组合，使用迭代求解最优的拟合误差。基于峰值拟合的方法gannet(edden ra,puts na,harris ad,etal.,"gannet:a batch-processing tool for the quantitative analysis of gamma-aminobutyric acid-edited mr spectroscopy spectra,"journal of magneticresonance imaging,40(6):1445-1452,2014.)，专门用于定量磁共振编辑谱，通过对波谱使用非线性最小二乘拟合，估计目标代谢物浓度。以上方法都难以避免最优化计算过程，并且易受伪影干扰，对目标波谱的质量要求较高，量化时间和量化结果稳定性难以保证。

3、近年来，深度学习在磁共振领域广泛发展。在离体磁共振波谱上，屈小波等(qu x,huang y,lu h,et al.,"accelerated nuclear magnetic resonance spectroscopy withdeep learning,"angewandte chemie international edition,132(26):10383-10386,2020.)首次提出并实现基于深度学习的快速高质量磁共振波谱重建人工智能方法。黄奕晖等(huang y,zhao j,wang z,et al.,"exponential signal reconstruction with deephankel matrix factorization,"ieee transactions on neural networks andlearning systems,doi:10.1109/tnnls.2021.3134717,2021.)提出一种基于hankel矩阵分解的深度学习指数信号重建方法。王孜等(wang z,guo d,tu z,et al.,"a sparsemodel-inspired deep thresholding network for exponential signalreconstruction-application in fast biological spectroscopy,"ieee transactionson neural networks and learning systems,doi:10.1109/tnnls.2022.3144580,2022.)提出了一个深度自适应阈值网络，运用稀疏最优化理论的同时结合深度学习，实现了鲁棒，高保真且计算成本低的波谱重建。在活体磁共振波谱上，陈棣成等(chen d,hu w,liu h,etal.,"magnetic resonance spectroscopy deep learning denoising using few invivo data,"arxiv preprint,arxiv:2101.11442,2021)利用深度学习实现了磁共振波谱低信噪比下的高保真去噪。磁共振领域持续致力于设计更可靠的波谱量化分析方法，特别是对于gaba等较为挑战的代谢物，以使mrs成为协助临床实践的有效工具。最近，chandler等人(chandler m,jenkins c,shermer s m,and langbein f c,"mrsnet:metabolitequantification from edited magnetic resonance spectra with convolutionalneural networks,"arxiv preprint,arxiv:1909.03836,2019.)首次利用神经网络对mega-press序列进行量化，但此方法基于“端到端”的网络学习来实现目标代谢物的浓度估计，缺乏一定的可解释性和泛化性证明(yang q,wang z,guo k,et al.,"physics-drivensynthetic data learning for biomedical magnetic resonance:the imagingphysics-based data synthesis paradigm for artificial intelligence,"ieeesignal processing magazine,40(2):129-140,2023)。

技术实现思路

1、本发明的目的在于利用磁共振信号的物理特性与深度学习网络，提供一种适合磁共振波谱的量化分析方法。本发明用于量化磁共振波谱，具有定量准确性高、定量结果稳定、泛化性好、减少预处理操作的特点。

2、本发明包括以下步骤：

3、1)基于量子演化模拟生成代谢物基集，添加如频率偏移、相位偏移、噪声的非理想因子，构建仿真数据集；

4、2)构建基于物理模型驱动的用于磁共振波谱定量的深度学习网络模型及损失函数，得到最优网络模型；

5、3)将利用谱编辑技术采集到的人体磁共振编辑谱作为输入数据，通过步骤2)中的最优网络模型，预测得到目标代谢物浓度和矫正后的输入谱。

6、4)利用步骤3)中预测的浓度，计算目标代谢物的相对浓度。

7、在步骤1)中，基于量子演化模拟生成代谢物基集，添加非理想因子，包括频率偏移、相位偏移、噪声，构建仿真数据集的具体方法为：

8、理想条件下采集的edit-on信号不包括零阶相位、频率偏移和噪声，理想磁共振edit-on信号可建模为磁共振时域信号模型b(nδt)，用公式表示为：

9、

10、其中，δt表示信号采样时间间隔，n表示信号长度，总长度为n；下标m表示第m种代谢物，m表示代谢物类别的总数，cm表示第m种代谢物的浓度，vm(nδt)对应edit-on信号第m种代谢物的基集信号。

11、理想磁共振edit-off信号可建模为磁共振时域信号模型s(nδt)，用公式表示为：

12、

13、其中，hm(nδt)对应edit-off信号第m种代谢物的基集信号。

14、添加非理想因子，包括频率偏移、相位偏移、噪声，使得仿真数据接近实测数据，非理想磁共振edit-on信号可建模为磁共振时域信号模型p(nδt)，用公式表示为：

15、

16、其中，εedit-on(nδt)表示edit-on信号的高斯白噪声，xm(nδt)表示edit-on信号的第m种代谢物分量信号，具体用公式表示为：

17、

18、其中，i表示虚数单位且i2＝-1，φ1和f1模拟非理想条件下导致edit-on信号产生的零阶相位和频率偏移。

19、非理想edit-off信号可建模为磁共振时域信号模型q(nδt)，用公式表示为：

20、

21、其中，εedit-off(nδt)表示edit-off信号的高斯白噪声，ym(nδt)表示edit-off信号的第m种代谢物分量信号，具体用公式表示为：

22、

23、其中，φ2和f2模拟非理想条件下导致edit-off信号产生的零阶相位和频率偏移。

24、每组仿真数据包含edit-on信号和edit-off信号，不同组仿真数据的代谢物浓度根据活体代谢物浓度范围随机分布；零阶相位值、频率偏移量根据实测数据设定合理范围，在合理范围内随机分布。同一组仿真数据的edit-on和edit-off信号施加相同的浓度和不同的零阶相位值、频率偏移量。

25、根据磁共振信号特点，同一组仿真数据取n＝0,1,2,3,...,n-1分别构成edit-on和edit-off谱的时域向量pt＝[p(0),p(1),...,p(n-1)]t和qt＝[q(0),q(1),...,q(n-1)]t，对这两个向量进行离散傅里叶变换，得到仿真的非理想edit-on、edit-off波谱pf和qf，维度为n×1；edit-on和edit-off谱相减，可以得到仿真的非理想编辑谱z，可以用公式表示为：

26、z＝pf-qf                                          (22)

27、其中，z维度为n×1，z作为网络训练的输入数据。

28、每组浓度[c1,c2,...,cm]t构成向量c，维度为m×1。

29、同一组仿真数据取n＝0,1,2,3,...,n-1分别构成edit-on和edit-off谱的时域向量bt＝[b(0),b(1),...,b(n-1)]t和st＝[s(0),s(1),...,s(n-1)]t，对这两个向量进行离散傅里叶变换，得到仿真的理想edit-on、edit-off波谱bf和sf，维度为n×1。

30、bf、sf、c三者共同构成标签{c,bf,sf}。

31、训练集由若干组{z,{c,bf,sf}}组成。

32、在步骤2)中，构建基于物理模型驱动的用于磁共振波谱定量的深度学习网络模型及损失函数，求解最优网络模型的具体方法为：

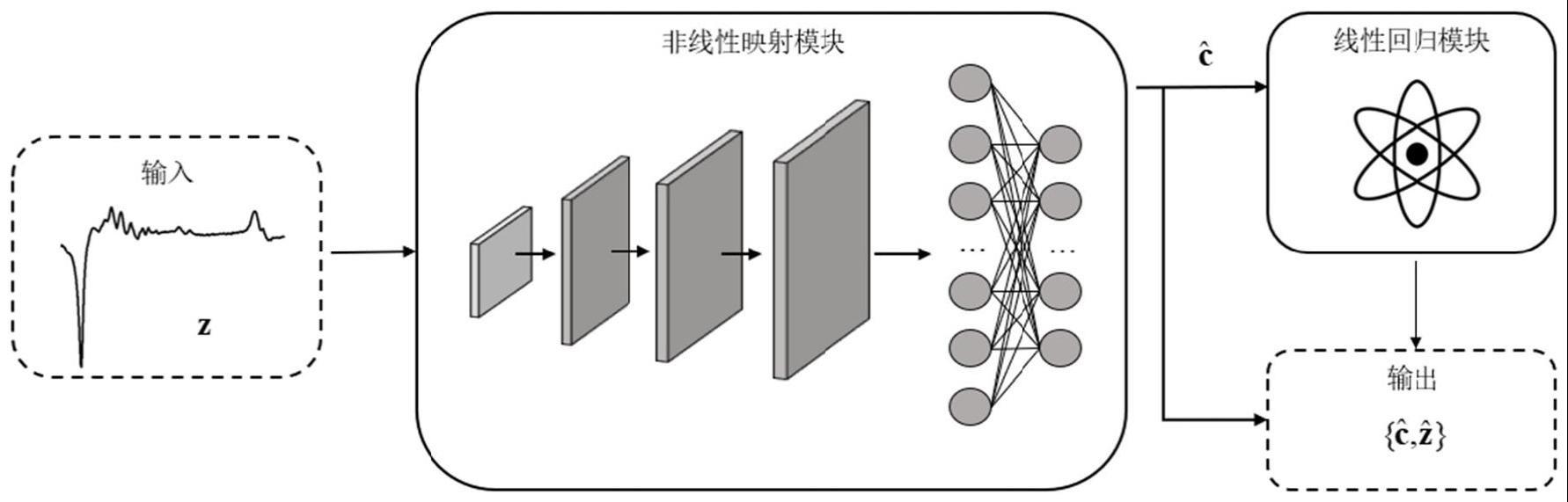
33、a)设计一个非线性映射模块，预测代谢物浓度系数该非线性映射模块由若干个卷积块和若干个全连接层组成。每个卷积块包含两个二维卷积层和一个最大池化层。非线性映射模块可表示为：

34、

35、其中，θ表示非线性映射模块的训练参数集合，表示从z到的非线性映射。

36、b)设计一个线性回归模块，获得矫正后的输入谱取n＝0,1,2,3,...,n-1构成edit-on和edit-off谱的基集信号时域分向量对向量进行离散傅里叶变换，得到edit-on和edit-off的基集分量信号波谱维度为n×1。将共2m个基集分量信号波谱按列排列成基集分量信号波谱矩阵维度都为n×m。该线性回归模块引入edit-on和edit-off谱的基集von、hoff作为物理先验，进一步约束网络，将a)模块预测的浓度系数和edit-on、edit-off谱的基集von、hoff代入公式(1)、(2)得到理想的edit-on、edit-off波谱和则矫正后的输入谱可以通过以下公式计算：

37、

38、因此，线性回归模块的功能可以用公式表示为：

39、

40、其中，表示从预测浓度到矫正后的输入谱的线性映射。

41、综上，整体网络将线性映射模块、非线性回归模块级联。整体网络可表示为：

42、

43、其中，表示从z到的非线性映射。

44、c)设计损失函数，损失函数值作为网络最优模型的评估指标，整体网络损失函数的定义为：

45、

46、其中，ω1和ω2是权重系数，ω3是网络中定义的batchsize的值，表示向量的2范数。

47、d)将步骤1)构建的仿真数据训练集输入网络，利用adam优化器，通过网络迭代训练，通过最小化损失函数loss(θ)获得最优参数集合下的最优网络模型。

48、在步骤3)中，将利用谱编辑技术采集到的人体磁共振编辑谱作为输入数据，通过步骤2)中的最优网络模型，预测得到目标代谢物浓度和矫正后的输入谱的具体方法为：

49、将采集的活体on和off谱p*、q*相减得到编辑谱z*，可表示为：

50、z*＝p*-q*                              (28)

51、将z*输入步骤2)中所述的最优参数集合下的最优网络模型，得到预测的目标代谢物浓度和矫正后的输入谱用公式表示为：

52、

53、在步骤4)中，利用步骤3)中预测的浓度，计算目标代谢物的相对浓度的具体方法为：

54、代谢物a和代谢物b与d的混合物的相对浓度计算可以表示为：

55、

56、其中，a∈{1,2,...,m},b∈{1,2,...,m},c∈{1,2,...,m},a≠b≠d；表示代谢物a的浓度，表示代谢物b的浓度，表示代谢物d的浓度。

57、本发明结合神经网络优越的非线性学习能力和磁共振信号模型的可解释性，可以快速精准量化γ-氨基丁酸等目标代谢物，有效减小了非理想因素造成的量化误差，提高了量化结果的稳定性。