针对带状线性系统上高斯消去的指数加速方法

本发明涉及针对带状线性系统上高斯消去的指数加速方法，属于计算机矩阵求解领域，尤其适用于带状线性系统上高斯消去的指数加速方法。

背景技术：

1、仿真模拟领域(如计算流体力学)的问题通常被规约为求解线性方程组ax＝b，a是尺寸为n×n的大型稀疏线性矩阵，x是n×1的由未知变元构成的列向量，b为n×1的偏置向量.此外，由实际问题规约而成的系数矩阵a通常具有特殊的属性与非零结构，如在计算流体力学领域，应用有限元方法离散化偏微分方程而得来的矩阵往往是正定厄米特矩阵(positive hermitiian definite，spd)；带状矩阵(banded matrix)通常出现在计算力学、计量经济学、人工智能、与纳米电子学领域，其带宽d通常远小于矩阵维度n，即d＜＜n.直接解法，比如高斯消去、qr方法，lu方法、cholesky方法通常应用于低维或稠密系数矩阵线性系统。在高维稀疏线性系统中，由于直接法难以并行求解同时舍入误差导致累计误差不可忽略，且在实际问题中往往不追求方程的精确解，所以通常用迭代解法以求解上述由实际问题引出的方程ax＝b的近似解.共轭梯度迭代法(conjugate gradient，cg)通常用于迭代求解对称正定系数矩阵的方程组，双共轭梯度(bicg)方法通常用于一般系数线性方程组的迭代求解，在精确计算下这两个方法都最终在第n步收敛.由于数值计算的精度会影响共轭方法中空间基的正交性，这通常导致cg与bicg方法在大规模问题求解时失效。为此，研究者提出了一系列的预处理方法来逼近所求系统的解.通常，预处理过程中蕴含求解一个带状系统解的问题。目前带状系统求解方法要么是串行求解，比如，带状系统高斯消去，迭代次数为o(n)，要么是一般的迭代方法，精确计算下从非特殊初值开始迭代到得到精确解的次数至少为n.本专利基于带状系统结构提出一种专用于带状线性系统的并行加速求解方法：一种基于分块矩阵的带状系统指数加速并行高斯消去方法。该方法既可以直接求解带状系统，也可以作为带状系统的预解算子，其并行迭代次数为o(log2n)，相对串行方法与传统迭代方法该方法具有指数加速效果.另外，我们也可以使用该方法以同样计算复杂度并行求解带状矩阵的逆矩阵。

2、综上所述，快速的带状线性系统的求解方法可以广泛应用于科学计算与过程计算的各个领域，比如可计算流体力学、博弈论、计量经济学、人工智能、计算生物学、分子动力计算、仿真模拟等等领域，加速计算过程、降低计算能耗，为低碳绿色计算提供新的技术支撑.

技术实现思路

1、有鉴于此，本发明提供及针对带状线性系统上高斯消去的指数加速方法，通过对矩阵进行分块，然后迭代地并行消去矩阵中的非零块，最终得到一个对角型分块矩阵，对最后矩阵并行求逆，根据这些矩阵直接的递归关系可得到原带状矩阵的逆矩阵为o(log2n)个稀疏矩阵的乘积，再使用矩阵向量乘积的并行计算求解带状线性系统.

2、为达到上述目的，本发明提供如下技术方案：

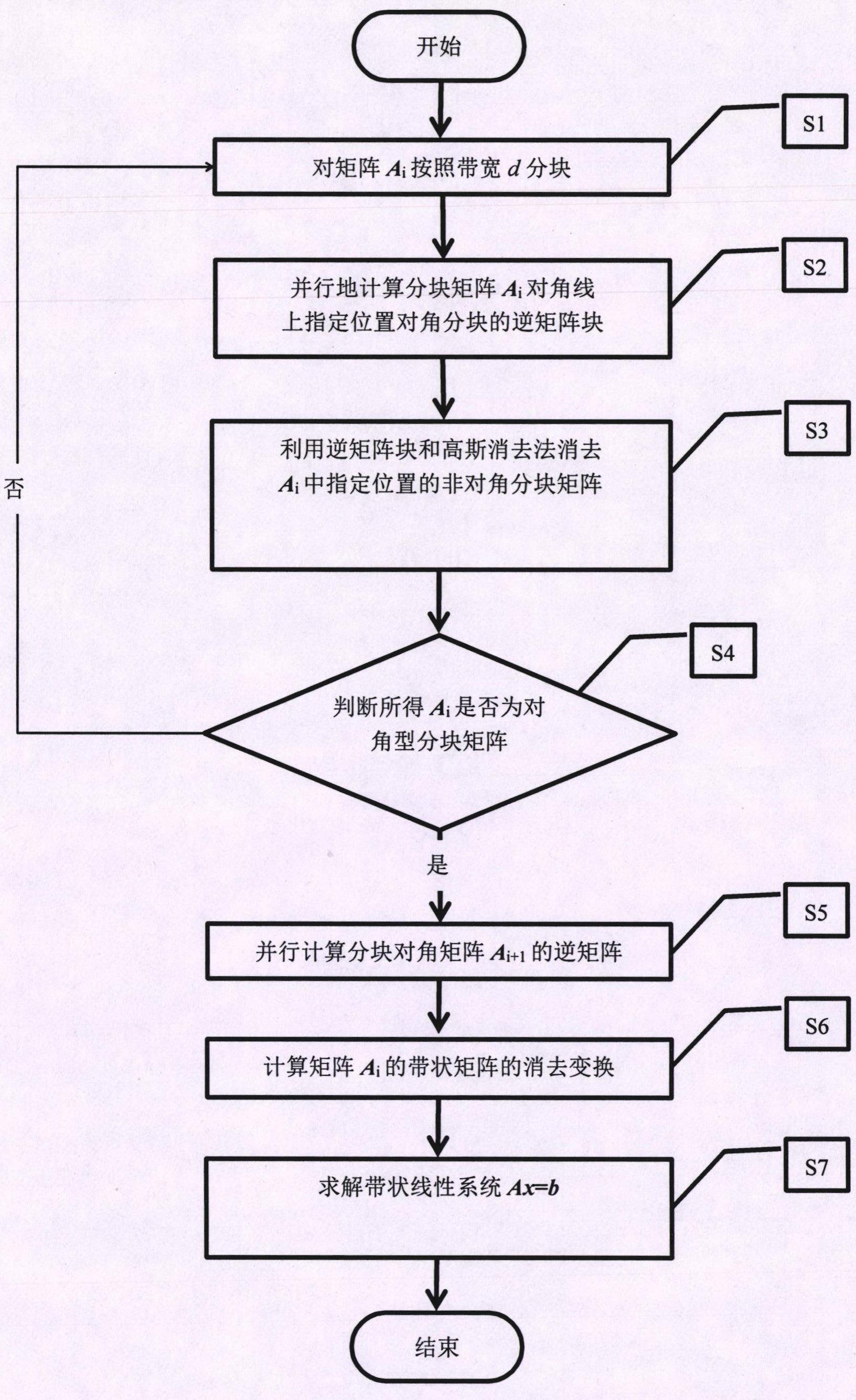
3、针对带状线性系统上高斯消去的指数加速方法，其特征在于，针对带宽为d的带状线性系统ax＝b，其中，a为n×n的正定带状厄米特矩阵，当所给带状矩阵不是正定厄米特矩阵时，可通过求解ahax＝ahb来求解ax＝b，此处ah表示a的共轭转置矩阵；x为n×1的未知数向量；b为n×1的偏置向量；d≥1是带状矩阵非零半区域的对角线条数，结合图1，该方法包含以下步骤：

4、s1：从a0＝a开始进行矩阵分块，按照d×d的大小将矩阵ai分割为不相交的分块矩阵；其中，i＝0，1，2，…为迭代次数；

5、s2：计算对角块中指定位置的分块矩阵对应的逆矩阵块，其中，对角块为包含了ai对角线元素的分块矩阵；

6、s3：利用逆矩阵块和高斯消去法消去ai中第行与列中非对角线上的非零分块处分块矩阵，得到矩阵ai+1，并保存相应的消去矩阵变换pi；

7、s4：如果步骤s3所得ai+1不是一个对角型分块矩阵，则重复步骤s1到s3，直到ai+1是一个对角型分块矩阵；

8、s5：令d＝ai+1，并行地计算分块对角矩阵d的逆矩阵d-1；

9、s6：根据步骤s3中的矩阵变换pl，0≤l≤i，得到带状矩阵的消去变换p＝п0≤l≤ipl满足关系paph＝d，其中ph是p的共轭转置矩阵；

10、s7：按照x＝phd-1pb，求解ax＝b；

11、所述的是集合ind0＝{1，2，…，n}的子集，其元素按从小到大排列，用来表示第i次迭代时ai需要消去的行与列，满足其具体的递归计算步骤为：从i＝0开始，将indi中所有处于奇数位置的元素提取出来，按从小到大排列构成新的集合将中所有处于偶数位置的元素提取出来，按从小到大排列构成新的集合indi+1；

12、所述的高斯消去法是矩阵ai的某个分块通过矩阵行变换或者列变换把指定分块变换为0分块矩阵.

13、进一步，步骤s1所述矩阵分块具体为：按照d×d的大小将矩阵ai分割为不相交的个分块矩阵；其中，ai的每一行和每一列至多有三个分块非零；当n/d不是整数时，无需对不足分块进行补充，最后的对角块dk，k大小为d’×d’，最后一行除dk，k以外的分块大小为d’×d，最后一列除dk，k以外的分块大小为d×d’，其中，为向上取整函数，d’＝nmod d，mod为取模函数。

14、可优选地，所述的步骤s2所述的逆矩阵块的计算可以采用并行计算，根据计算机的处理器个数p和第i次迭代时的元素个数决定的，进行轮的并行计算.具体地，如果的元素个数小于等于p则任意选择个处理器，每个处理器计算一个ai的对角分块dj，j的逆矩阵即可，如果的元素个数大于p则我们需要进行如下的轮并行计算，第m(1≤m＜p)个处理器计算中的第至个元素对应的分块的逆矩阵，第p个处理器计算中剩下元素对应的分块的逆矩阵。

15、进一步，步骤s3所述的高斯消去法可采用并行计算，具体为并行的进行如下操作：(1)当且不是其中最小或者最大元素时，利用步骤s2求得的对角块bj，j的逆矩阵块并行的消去对角块bj，j上、下、左、右紧邻的四个非零分块矩阵当是的最小元素时，只需利用步骤s2求得的对角块bj，j的逆矩阵块消去对角块bj，j下、右紧邻的两个非零分块矩阵与当是的最大元素时，只需利用步骤s2求得的对角块bj，j的逆矩阵块消去对角块bj，j上、左紧邻的两个非零分块矩阵与

16、具体地，使用逆矩阵消去的方法是在矩阵ai左乘以下矩阵其中，i为单位矩阵。

17、

18、使用逆矩阵消去的方法是在矩阵ai左乘以下矩阵

19、

20、类似地，使用逆矩阵消去的方法是在矩阵ai右乘矩阵使用逆矩阵消去的方法是在矩阵ai右乘以下矩阵

21、上述消去时，ai+1的元素计算公式如下；ai+1[j-，j]＝ai+1[j+，j]＝ai+1[j，j-]＝ai+1[j，j+]＝0，其它分块位置的元素值不变.特别指出，当j是的最小元素时，对ai不做左乘以下矩阵以及左乘以下矩阵为方便可令为单位矩阵；当j是的最大元素时，对ai不做左乘以下矩阵以及左乘以下矩阵为方便可令为单位矩阵：如果indi包含三个以上元素，我们取如果indi只有两个元素时，任意取或者其中一个即可把ai变换为对角型分块矩阵，保存pi；通过并行地计算ai+1的元素如下：对以及对令中比j小的最大数，令是中比j大的最小数，j-*为中比j小的最大数，j+*为中比j大的最小数，则其它位置上ai+1与ai的分块矩阵一样.

22、可优选地，所述的利用对角块的逆矩阵消去非零分块矩阵的方法也是高斯消去法，可以采用并行计算加速。

23、由于对称性，只需要计算个分块矩阵即可，具体并行方式如下；结合图2，如果#i≤p则任意选择#i个处理器，每个处理器计算一个ai+1中的ai+1[j，j]或者即可，如果#i＞p则我们需要进行如下的轮并行计算，每一轮并行计算中p个处理器计算ai+1中的p个ai+1[j，j]或者直到所有ai+1需要计算完的分块为止；令与

24、可优选地，所述的步骤s5可以采用并行计算来加速计算分块对角矩阵d的逆矩阵d-1。

25、进一步，步骤s6根据所有步骤s3中的矩阵变换pl，0≤l≤i，以及递归关系可得：

26、

27、进一步，步骤s7据步骤s5中矩阵a与d的关系以及步骤s6的结果可得

28、

29、使用步骤s5所计算的d-1得到带状矩阵a的逆矩阵计算公式

30、

31、以此逆矩阵计算公式求解ax＝b，即：

32、

33、可优选地，所述的步骤s7中＝phd-1pb的矩阵乘法可以采用并行计算加速，从矩阵乘积的右侧开始连续并行计算矩阵向量乘积直到计算出x的数值.

34、本发明的有益效果在于：本发明提供了针对带状线性系统上高斯消去的指数加速方法，基于矩阵分块，以及并行高斯消元方法的思想，每次消去方程组中一半左右未知元，迭代地并行消元，最终至多次并行迭代后，一定转化为对角的分块矩阵，从而实现带状线性系统的精确求解，比现有的方法高斯迭代方法以及各种共轭梯度方法的迭代次数o(n)量级降低了计算量，使得计算效率指数级的提升，而且求解过程中的矩阵逆都在低阶矩阵上进行，使得本发明方法能高效、高精度求解带状线性系统.