一种车轮多边形状态识别方法和系统

本发明涉及轨道交通，特别涉及一种车轮多边形状态识别方法和系统。

背景技术：

1、城市轨道交通中的地铁车辆在运行过程中，车轮是链接列车与路轨、承载列车重量以及受力的最重要构件，因此车轮和路轨的接触状态与列车行驶是否平稳、乘客是否舒适、安全息息相关。

2、车轮在运行过程中往往会因为侵蚀、轮轴共振、磨损和行车特性等原因产生不同形式的磨损，而其中表现车轮不圆顺的主要特征为车轮多边形现象。而车轮上不同阶数的多边形会对车辆行驶造成不同程度的影响，因此建立一种有效的方法对车轮多边形情况进行分析具有很高的重要性。

3、轨道交通中用于检测车轮磨损的方法主要分为两种。一是轨旁式动态检测法，其主要是利用各种类型的传感器对路轨状态进行监测，主要采用轮轨力检测法、激光与机器视觉检测法和声面状态，但抗干扰能力差，精度低，不能很好反映车轮多边形情况而且成本高，技术难度大很难成规模进行推广；另外一种车轮磨损检测方法为车载式动态检测法，通过将传感器直接安装在车辆的轴箱和转向架上进行车轮的不间断监测，实时获取车辆行驶数据进而对车轮故障进行定量定位分析，但是车载式动态监测法采集通道多，数据量大，实用性仍有不足，并且安装在轴箱处会受到轴承振动以及其他结构振动的影响，导致识别精度较低。

技术实现思路

1、针对现有技术中车轮多边形状态识别精度低的技术问题，本发明提出一一种车轮多边形状态识别方法和系统，通过对地铁车辆轴箱处的振动状况进行信号采集和故障监测，从而判别车轮多边形所处状态，提高了识别精度。

2、为了实现上述目的，本发明提供以下技术方案：

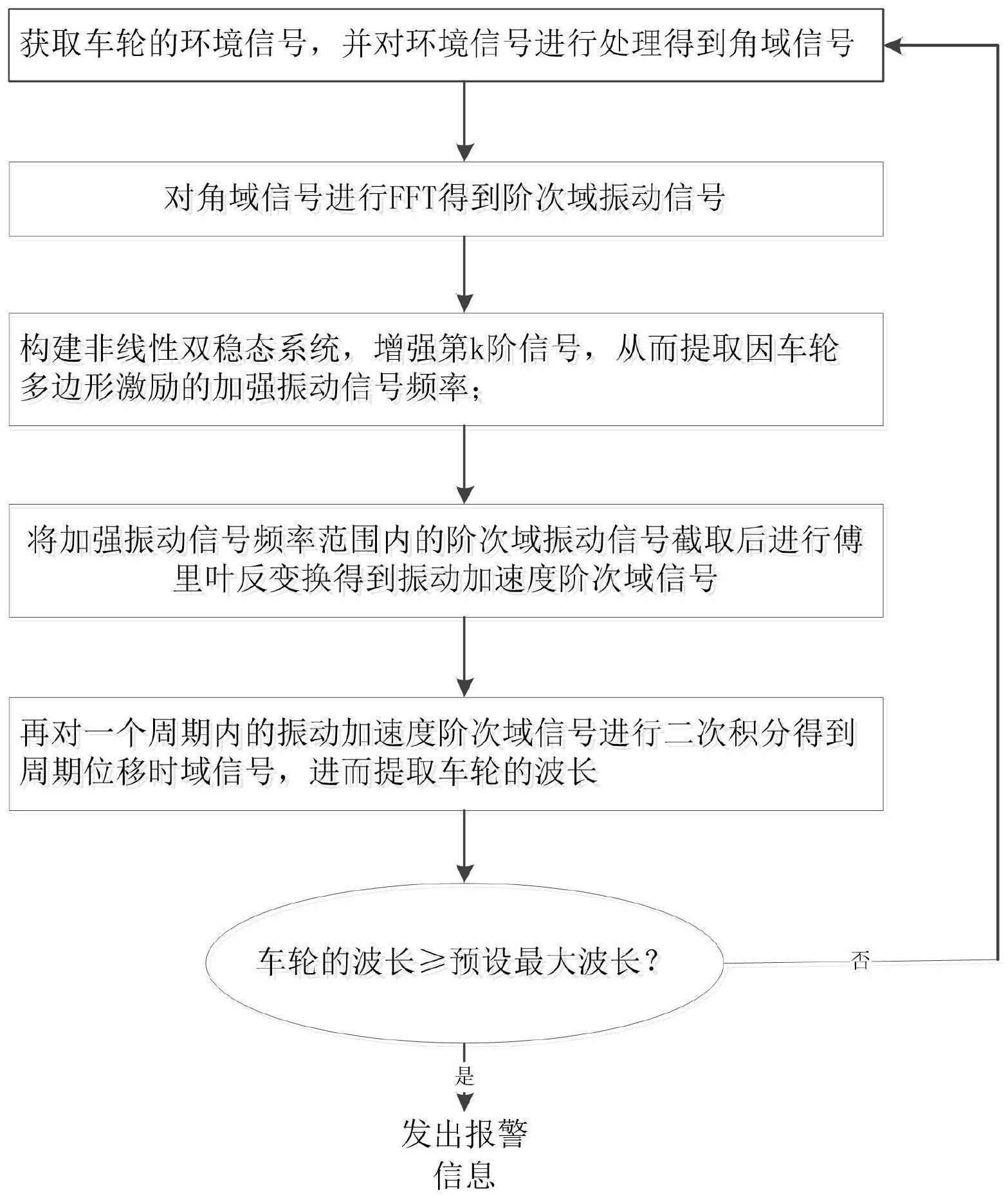
3、一种车轮多边形状态识别方法，包括以下步骤：

4、s1：通过增量型编码器获取车轮的角域信号；

5、s2：对角域信号进行fft得到阶次域振动信号，再根据阶次域振动信号构建非线性双稳态系统，增强第k阶信号，从而提取因车轮多边形激励的加强振动信号频率；

6、s3：将加强振动信号频率范围内的阶次域振动信号截取后进行傅里叶反变换得到振动加速度阶次域信号，再对一个周期内的振动加速度阶次域信号进行二次积分得到周期位移时域信号，进而提取车轮在周期内的最大波长；

7、s4：将s3中车轮在周期内的最大波长与预设最大波长进行比较，当车轮在周期内的最大波长不小于预设最大波长时，车轮处于故障状态，提出预警、报警信息。

8、优选地，所述s1中，环境信号包括振动信号、轴箱机械构件所产生的有色噪声以及环境中的白噪声。

9、优选地，所述s1中，对环境信号进行处理的方式为：

10、在车辆轴箱处安装增量型编码器，车轴旋转时增量型编码器的光栅发生变化，从而产生采样脉冲，再通过采样脉冲触发采集信号；由于采样脉冲频率对应增量型编码器分辨率且由于增量型编码器分辨率转角确定，从而得到对应的角域信号。

11、优选地，所述s2包括：

12、s2-1：对角域信号进行fft可以得到阶次域振动信号：

13、

14、公式(2)中，s(k)为阶次域振动信号；s(θn)为角域信号；n表示信号长度；k表示阶次变量；表示复指数常量；n表示阶次域振动信号的阶次；j表示复数常量；

15、s2-2：构建非线性双稳态系统，对振动信号进行增强，从而提取多边形激励的振动信号频率；

16、非线性双稳态系统的langevin方程表示为：

17、

18、公式(3)中，a、b表示状态参数；x为非线性双稳态系统变量；k为阶次变量；s(k)表示阶次域振动信号；γ(k)表示阶次域噪声信号，d表示噪声强度，ξ(k)为零均值的高斯白噪声，满足数学期望e(γ(k))＝0，表示相位移动。

19、优选地，所述s2-2中，a、b的求取方法为：

20、a、设阶次域振动信号的阶次为1-12，计算得到阶次域振动信号的阶次功率：

21、

22、公式(5)中，ps表示阶次域振动信号的阶次功率；n表示阶次域振动信号的阶次；k表示阶次变量；s(k)用参数a、b表达，s(k)表示阶次域振动信号；γ(k)表示噪声信号；

23、b、根据阶次功率得到信噪比：

24、snr＝10log(ps/pn)                              (5)

25、公式(5)中，snr表示信噪比；ps表示阶次域振动信号的阶次功率；pn表示整个阶次域中信号功率，计算公式为：

26、c、令a、b∈[k1，k2]，k1、k2分别表示取值下限、上限，a和b均以δ＝(k2-k1)/n为梯度计算s(k)，并计算对应snr(i,j)值，从而生成信噪比粒子群矩阵，并给出对应初始速度矩阵其中v(i,j)＝1：

27、

28、公式(6)中，pop表示信噪比粒子群矩阵；snr(i,j)表示通过第i个a，第j个b计算得到的信号信噪比，v(i,j)表示对应信噪比粒子的初始速度；

29、d、设迭代次数为m，适应度阈值为ω，最大允许迭代步数为t，适度函数选择为pi＝max{snr(i,j)|snr(i,j)∈pop}，则迭代速度计算公式为：

30、

31、公式(7)中，表示迭代速度；ωi表示适应度阈值，表示粒子移动速度，c1、c2表示两个正常数，rand1，rand2表示两个独立的、介于[0，1]之间的随机数，pbesti表示优化解；表示第i个粒子，gbesti表示全局最好适应度函数值，i表示粒子序号，d表示维度参数，m表示迭代次数；

32、e、计算每个粒子的适应函数值pi，并与优化解pbesti进行比较：若pi<pbesti，用新的粒子替代前一轮粒子，即令pbesti＝snri，再与全局最好适应度函数值gbesti进行比较，若pi≥pbesti继续寻找下一个粒子进行比较；若pi<gbesti则取代每个粒子，pbesti＝gbesti＝snri，并保存当前状态进行下一次迭代计算，若pi≥gbesti继续寻找下一个粒子进行比较：

33、pi＝max{snri,j|snr(i,j)∈pop}；

34、f、迭代完成后，输出全局最好适应度解snr(i,j)，得到其对应的状态参数a、b。

35、优选地，所述s3包括：

36、s3-1：将多边形激励的加强振动信号频率范围内的阶次域振动信号通过构建的阶次域带通滤波器：

37、

38、公式(8)中，hk表示构建的阶次域带通滤波器；k表示阶次；

39、s3-2：将通过滤波器的阶次域振动信号进行傅里叶逆变换，得到车轮多边形效应产生的加速度角域信号：

40、

41、公式(9)中，aθ表示加速度角域信号；s1k表示通过带通滤波器的阶次域振动信号，k表示阶次变量；θ表示θ表示角域信号自变量；j表示复数常量；

42、s3-3：对加速度角域信号进行二次积分得到周期位移时域信号，计算公式如下：

43、

44、公式(10)中，xθ表示周期位移时域信号；aθ表示加速度角域信号。

45、优选地，所述s4中，车轮在周期内的最大波长计算公式为：

46、λtmax＝maxxθ-minxθ(11)

47、公式(16)中，λtmax表示车轮多边形在周期内的最大波长；maxxθ表示最大周期位移时域信号；minxθ表示最小周期位移时域信号。

48、本发明还提供一种车轮多边形状态识别系统，包括：

49、信号获取单元，用于获取车轮的环境信号并将其处理为角域信号；

50、第一转换单元，用于将角域信号转换为阶次域振动信号；

51、非线性双稳态系统构建单元，用于根据阶次域振动信号构建非线性双稳态系统，提取多边形激励的振动信号频率；

52、信号截取单元，用于根据振动信号频率截取频率范围内的阶次域振动信号；

53、第二转换单元，用于将振动信号频率范围内的阶次域振动信号转换为加速度角域信号；

54、第三转换单元，用于将加速度角域信号转换为周期位移时域信号；

55、状态监测单元，用于将获取的车轮多边形的波长λ与预设最大波长λmax进行比较，当λ≥λmax，则提出预警、报警信息。

56、本发明还提供一种计算机存储介质，所述计算机存储介质上存储有计算机程序，该计算机程序被处理器执行时实现一种车轮多边形状态识别方法的步骤。

57、综上所述，由于采用了上述技术方案，与现有技术相比，本发明至少具有以下有益效果：

58、本发明利用角域随机共振(sr)的方法可以在变转速工况下从地铁列车行驶环境包含的强噪声中提取出由车轮多边形振动激励产生的信号，再利用提取出的信号进行傅里叶逆变换以及二次积分处理，可极大的增加对车轮多边形阶数以及波深判断的正确率以及精度。