一种数据驱动的飞机复杂薄壁结构装配公差优化设计方法

本发明涉及飞机装配特征偏差数字化协调，尤其涉及一种数据驱动的飞机复杂薄壁结构装配公差优化设计方法。

背景技术：

1、随着我国航空事业的飞速发展，飞机等航空产品呈现出装配零件数量众多、生产批量小、装配协调关系复杂、装配质量要求高等特点，产品的装配阶段占据了航空产品研制过程中的大量工时与成本，是整个飞机研制生产过程中关键的环节。装配成本是决定飞机生产制造成本的一个重要指标，在满足设计功能及性能要求的前提下，对产品装配公差进行合理分配能够极大地降低产品制造成本。

2、产品的公差优化设计过程是在确保产品装配质量、功能及性能要求的基础上，依据合适的优化方法在相应的约束条件下对装配公差进行合理分配，以缩减产品的制造成本。传统的装配公差优化设计主要是依据相关标准或设计人员的经验等方法进行，易出现几何精度设计不合理导致零件返工、零件互换性差以及装配精度难以满足等问题。从而不仅影响了产品的性能，而且导致材料的损耗，直接提高了产品的生产成本。

3、飞机复杂薄壁结构在装配过程中会产生可靠有效数据，这些数据蕴含了丰富的装配偏差传递、累积信息。充分挖掘利用这些数据信息，有助于我们进行装配偏差分析。粒子群优化算法来源于对生物群体社会性行为研究，通过群体中个体之间的信息传递，带领群体向问题最优解方向移动。随机初始化一些粒子，将粒子位置看作为问题的解，然后通过不断更新迭代求解出全局最优解，其具有搜索速度快、效率高等特点。基于上述分析，本发明提出了一种数据驱动的飞机复杂薄壁结构装配公差优化设计方法。该方法通过采集装配过程中的偏差检测数据，融合熵权法与马氏距离得到包含权重的装配质量综合值。然后，以产品的综合制造成本为优化目标，以所选加工方法的经济加工精度与装配质量要求为约束，建立飞机复杂薄壁结构的制造成本—公差数学模型。最后，利用粒子群优化算法对飞机复杂薄壁结构的制造成本—公差模型进行求解，得到满足产品装配质量且符合经济加工精度的各装配公差最优解，使得产品制造成本最低，完成装配公差的优化设计。

技术实现思路

1、本发明的目的在于解决现有技术中存在的技术问题，提供一种数据驱动的飞机复杂薄壁结构装配公差优化设计方法。

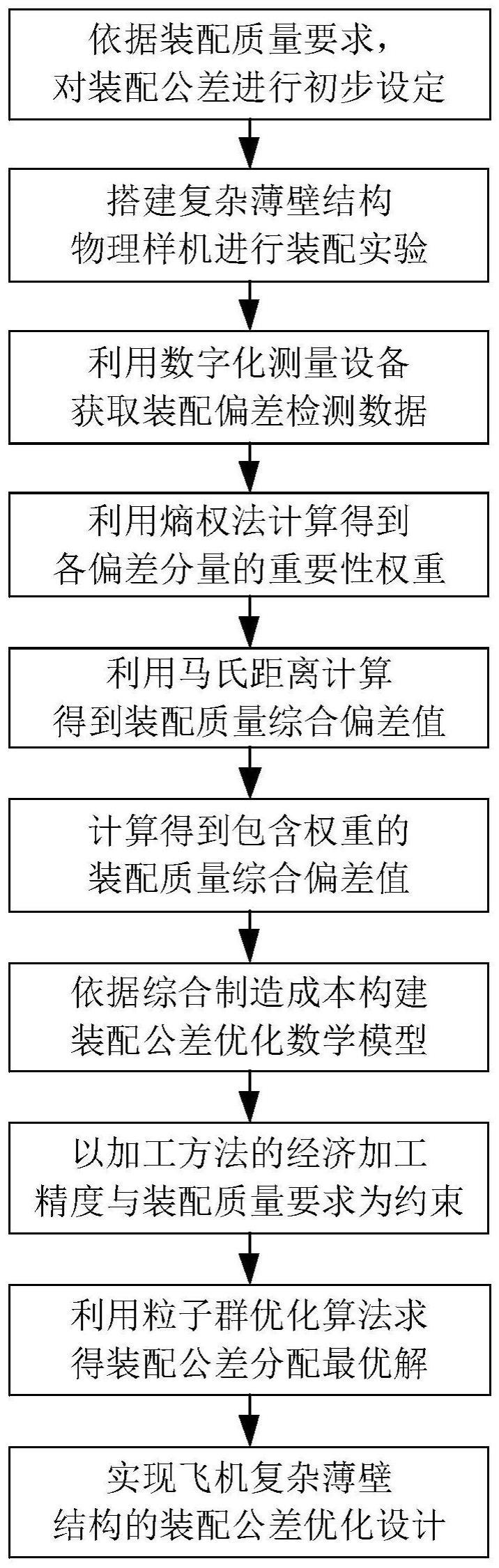
2、为实现上述目的，本发明提供的技术方案是：一种数据驱动的飞机复杂薄壁结构装配公差优化设计方法，该方法包括以下步骤

3、s100：根据飞机复杂薄壁结构装配质量要求，设计人员依据经验初步设定各零件装配公差；

4、s200：搭建飞机复杂薄壁结构物理样机，采集各偏差分量装配偏差检测数据；

5、s300：依据各偏差分量装配偏差检测数据，利用熵权法对各偏差分量赋予权重；

6、s400：融合熵权法与马氏距离，计算出包含偏差分量权重的飞机复杂薄壁结构装配质量综合偏差值；

7、s500：以综合制造成本为优化目标，建立公差优化数学模型；

8、s600：基于粒子群优化算法对建立的公差优化数学模型进行求解，得到装配公差最优解，实现飞机复杂薄壁结构装配公差的优化设计。

9、优选的，所述步骤s100中的初步设定各零件装配公差的具体方法为：

10、s101：设定飞机复杂薄壁结构的零件函数g：

11、g＝sa{a1,a2,…,am}

12、其中，g为飞机复杂薄壁结构；m为装配零件的个数；am为第m个装配零件；

13、s102：依据步骤s101，确定各零件的装配特征，再根据飞机复杂薄壁结构装配质量要求，设计人员依据经验初步给出各零件装配特征的公差数值，构建装配特征公差数据序列t；

14、t＝{t1(0),t2(0),…,ts(0)}

15、其中，s为装配特征的个数；ts(0)为第s个装配特征的公差初定值。

16、优选的，所述步骤s200中的采集装配偏差检测数据的具体方法为：

17、s201：搭建飞机复杂薄壁结构物理样机；

18、s202：依据初步设定的装配公差分配值，制造出步骤s101中所述的装配零件，然后装配得到飞机复杂薄壁结构物理样机，采集样机各偏差分量的装配偏差检测数据，构建各偏差分量的装配偏差检测数据序列δ

19、δi＝{xi(1),xi(2),…,xi(n)} i＝1,2,…,l

20、其中，δi为第i个偏差分量的偏差检测数据序列；n为装配次数；l为偏差分量的个数；xi(n)为第i个偏差分量第n次装配的偏差检测数据。

21、优选的，所述步骤s300中的对各偏差分量赋予权重的具体方法为：

22、s301：依据步骤s202中采集的各偏差分量装配偏差检测数据，构建偏差分量多属性评价矩阵q；

23、

24、其中，xl(n)为第l个偏差分量第n次装配的偏差数据；

25、s302：构建各偏差分量数据权重矩阵p

26、

27、其中

28、

29、其中，pi(j)为第i个偏差分量第j次装配的偏差实测数据所占权重；i＝1,2,…,l；l为偏差分量的个数；j＝1,2,…,n；n为装配次数；

30、s303：各偏差分量信息熵求解：

31、

32、其中，hi为第i个偏差分量的信息熵；

33、s304：偏差分量差异性系数求解：

34、ei＝1-hi i＝1,2,…,l

35、其中，ei为第i个偏差分量的差异性系数；

36、s305：偏差分量权重求解：

37、

38、其中，ωi为第i个偏差分量的权重。

39、优选的，所述步骤s400中的计算包含偏差分量权重的飞机复杂薄壁结构装配质量综合偏差值的具体方法为：

40、s401：将飞机复杂薄壁结构装配质量的目标值记为um＝(y1,y2,…,yl)，装配质量实测值记为ur＝(x1,x2,…,xl)，利用马氏距离计算飞机复杂薄壁结构装配质量综合偏差值d：

41、

42、其中，k为装配质量的协方差矩阵

43、

44、其中

45、

46、其中，a,b∈{1,2,…,l}，n为装配次数；xa(j)为第a个偏差分量第j次装配的偏差检测数据；xb(j)为第b个偏差分量第j次装配的偏差检测数据；分别为该偏差分量整体样本的平均值；

47、s402：依据步骤s305获取的偏差分量权重对步骤s401中的马氏距离公式进行改进，得到熵权—马氏距离计算公式：

48、

49、其中，d*为包含偏差分量权重的飞机复杂薄壁结构装配质量综合偏差值。

50、优选的，所述步骤s500中的建立公差优化数学模型的具体方法为：

51、s501：加工成本是指为满足飞机复杂薄壁结构装配质量满足要求，在零件加工制造时所投入的成本，构建如下所示的指数型加工成本—公差数学模型

52、

53、其中，cm为产品装配特征的加工成本；a0与a1为模型参数，由装配特征类型确定；tμ为第μ个装配特征的公差值；

54、s502：质量损失成本是指飞机复杂薄壁结构与目标装配质量存在偏差时，均会出现质量损失，构建如下所示的质量损失成本—公差数学模型

55、

56、其中，cs为产品的质量损失成本；d为产品不合格时所造成的质量损失成本；t/2为产品质量的临界偏差值；

57、s503：质量保证成本是指为了保证产品装配质量与性能而增加的投入，构建如下所示的质量保证成本—公差数学模型

58、

59、其中，cb为产品的质量保证成本；λμ与ξμ为与tμ无关的模型相关系数；

60、s504：飞机复杂薄壁结构制造成本主要包含加工成本、质量损失成本与质量保证成本，依据步骤s501～s503，构建如下所示的飞机复杂薄壁结构公差优化数学模型

61、

62、其中，f(tμ)为公差优化数学模型；

63、s505：基于所选加工方法的经济加工精度与装配质量要求，构建如下所示的公差优化数学模型的约束条件：

64、

65、其中，ti(min)第i个特征的经济加工公差下界，ti(max)第i个特征的经济加工公差上界；m0为产品装配质量满足功能性要求的偏差极限值。

66、优选的，所述步骤s600中的获取装配公差最优解的具体方法为：

67、s601：依据粒子群优化算法对步骤s504和s505构建的优化方程进行求解，定义待优化的各装配特征公差值为粒子的位置，公差值的变化率为粒子的速度；种群中各粒子的位置与速度定义如下：

68、

69、其中，n为种群的粒子数量；t(k)为第k代各粒子的位置序列；vt(k)为第k代各粒子的速度序列；

70、s602：对各粒子的位置进行随机初始化处理：

71、t(0)＝t(min)+λ·{t(max)-t(min)}

72、式中，t(max)与t(min)分别为特征公差的最大值与最小值，λ为[0,1]区间内的随机数；

73、s603：依据步骤s602中的初始化计算公式，计算初始个体最优局部位置与初始全局最优位置：

74、

75、其中，pbest t(0)为各粒子的初始个体最优位置，gbest t(0)为初始全局最优位置；

76、s604：为求解步骤s504中的公差优化数学模型最小值，对粒子最优位置不断更新：

77、

78、其中，pbest tν(k+1)为第ν个粒子进化到第k+1代时的个体最优位置；f(tν(k+1))为第ν个粒子进化到第k+1代时对应的综合制造成本；粒子的位置与速度更新方法为：

79、

80、其中，μ＝1,2,…,s，ν＝1,2,…,n，k表示粒子进化的代数；为第ν个粒子进化到第k+1代时第μ个特征公差方向的速度分量；为第ν个粒子进化到第k+1代时第μ个特征公差方向的位置分量；c1与c2为加速因子，r1与r2为[0,1]上的随机数；

81、s605：依据步骤s604获取的粒子全局最优位置，计算得到各装配特征公差修正量：

82、δtμ＝|gbest tμ(z)-tμ(0)|

83、其中，δtμ为第μ个装配特征的公差修正量；z为粒子更新的代数；gbest tμ(z)为第μ个特征公差的全局最优值；tμ(0)为第μ个特征公差的初始设定值。

84、本发明有益效果：

85、本发明以物理样机获取的装配偏差检测数据为基础，结合熵权法、马氏距离与粒子群优化算法等，提出一种数据驱动的飞机复杂薄壁结构装配公差优化设计方法。该方法以综合制造成本为优化目标，以所选加工方法的经济加工精度与装配质量要求为约束，构建出复杂薄壁结构制造成本—公差函数，并利用粒子群优化算法求解得到装配公差最优解。依据本发明提出的优化设计方法，不仅考虑了各偏差分量重要程度的差异，而且可以计算出装配公差最优解，在保证飞机复杂薄壁结构装配质量满足要求的同时，最大化降低制造成本，为飞机复杂薄壁结构等多质量属性产品的质量控制提供一种新的解决途径。