一种基于MIC-Stacking集成学习的高维小样本产品质量预测方法

本发明提供一种基于mic-stacking集成学习的高维小样本产品质量预测方法，属于质量预测领域，适用于高维小样本质量预测。

背景技术：

1、现代制造业产品更新速度加快，大规模单一的产品生产已不能满足市场的不同需求。企业在适应市场变化的同时降低运营成本，以获得竞争优势，越来越多的企业建立了灵活的生产线，寻求建立小批量生产模式。多品种、小批量生产正迅速成为我国制造业的主要生产方式，占我国制造业的90% 以上。

2、多品种、小批量生产模式下，由于单批量生产连续下降，很难提取大量的质量信息，质量数据相对稀缺，生成的数据信息的组成也更加复杂。这种生产模式带来了高维度、小样本质量的信息数据。

3、机器学习的预测技术，已成为当前质量控制技术的关键方向之一。企业可以从生产过程中收集多源数据。在对数据进行处理和分析之后，可以从制造过程，生产系统和设备中获得有价值的信息。这些技术实现了先进的产品制造质量预测，取代了之前的生产质量后检测方法。它可以提前发现和消除隐藏的质量危害，有效降低企业质量控制的成本。制造质量预测还为可靠性评估和参数优化提供数据支持，从而提高企业的智能管理水平。

4、本发明在机器学习模型基础上，利用mic-stacking集成学习模型解决了单一机器学习容易过度拟合，预测精度低和模型鲁棒性弱的问题。集成的方法可以利用不同的模型来获得更好的预测结果。集成学习具有更好的泛化能力和稳定性，并且结合具有独特特征的不同模型来解决单个模型的局限性，从而提高预测性能。mic改进基本模型的选择方法，有效识别线性和非线性关系，使预测模型的集成更加稳健准确。

技术实现思路

1、本发明的目的是提供一种基于mic-stacking集成学习的高维小样本产品质量预测方法，以解决目前高维、小样本数据质量预测精度低、鲁棒性弱的问题。，首先使用箱线图，最小二乘法（ols）和链式方程（mice）的多元插补来检测和替换异常值。然后利用最大信息系数（mic）用于获得基础学习模型之间的相关性。选择相关性低，预测能力强的模型建立堆叠集合模型的第一层，利用catboost算法构建第二层模型。本发明能够有效整合不同基准模型的优势，其预报性能明显好于单个机器学习模型。

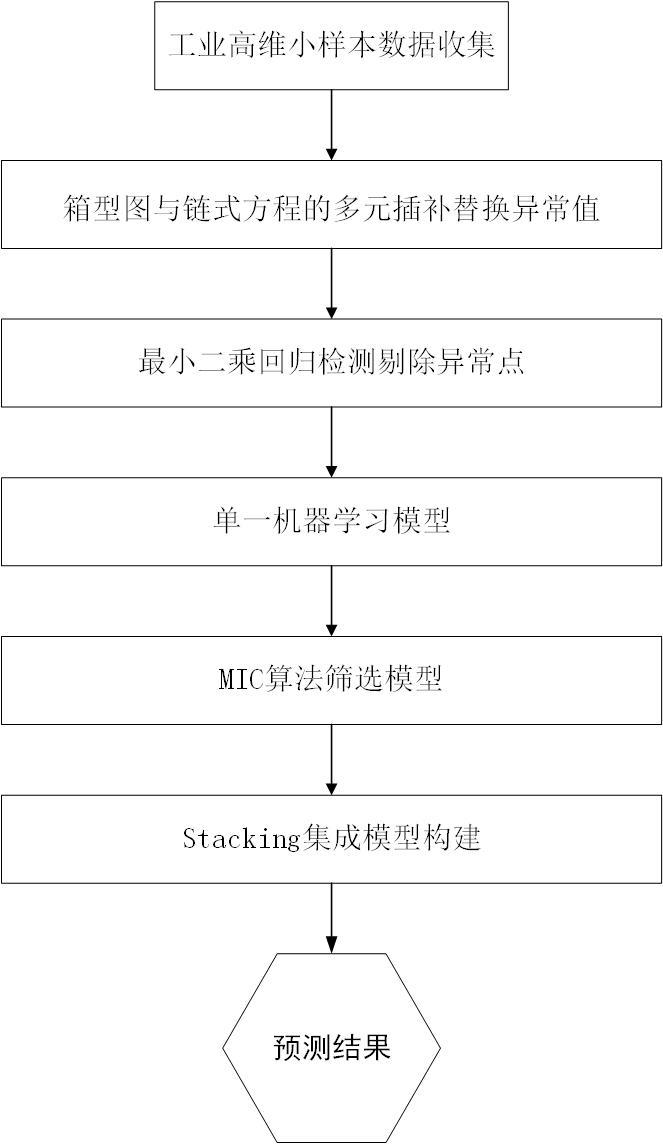
2、本发明为解决上述问题提供了一种基于mic-stacking集成学习的高维小样本产品质量预测方法，如附图1所示，该方法包括以下步骤：

3、步骤1：通过智能生产过程中获取的高维质量数据信息，包含若干过程参数和产品质量参数等质量特性，这些影响产品整体质量水平的重要因素及质量标准，从而构建最终产品质量数据集；

4、步骤2：高维小样本处理方法的处理条件更加复杂和多变，经常出现异常数据异常值和设备偏移误差。导致预测过程受到异常值的影响并影响最终的质量预测效果。在这项工作中，我们利用一种基于箱型图技术和链式方程的多元插补（mice）的方法进行迭代插补数据来替换异常值。该方法不受数据类型的影响，对数据的整体分布影响不大；

5、步骤3：使用最小二乘法（ols）来计算学生化残差、杠杆、库克距离和dffits来确定异常样本，识别出原始数据的异常点（强影响点），并进行剔除；

6、步骤4：输入训练数据通过k折交叉验证构建的模型进行训练，通过随机搜索和网格搜索算法的组合来选择参数，采用不同的评估标准来评估基础模型性能；

7、步骤5：mic用于计算各基础机器学习模型预测误差相关度，筛选差异较大的基础模型，构建差异最大化的stacking集成模型，充分利用不同模型中不同的数据观测值，避免相似模型重复学习；

8、步骤6：利用测试数据集输入构建的模型差异最大化的stacking得到质量预测结果。

9、其中，在步骤1中所述“产品质量数据集”，是指某一产品而言，具有一定数量的质量特性、一定数量的样本和每个样本明确质量数据的数据集。

10、其中，在步骤2中所述“基于箱型图技术和链式方程的多元插补（mice）的方法进行迭代插补数据来替换异常值”，具体方法如下：

11、2-1 ：箱型图技术异常值的判定标准为:，其中q1为下四分位(25%四分位)，q3为上四分位(75%四分位)，四分位范围(iqr)是指25%和75%四分位之间的差值，如附图2所示；

12、2-2 ：mice为每个缺失数据的变量分别定义一个预测模型，其基本思想如下：

13、（1）用初始估计值来填充缺失的值，通过从现有观察值中随机取样；

14、（2）对于每个缺失值，使用其他变量的观测部分作为预测因子来估计回归模型；

15、（3）缺失的值被从结果后验预测分布中随机抽取的值代替。使用观察到的和最近估计的估算值作为预测值，对每个缺失数据的变量重复这一过程；

16、给定以下带有p个不完全变量的数据集，将x的观测部分定义为，而x的缺失部分为；

17、其中是描述的条件密度的参数，为中的每个不完整变量迭代绘制插补,首先模拟参数的随机抽取，然后模拟变量中缺失值的随机抽取。通过观测数据的gibbs迭代抽样建立关于缺失变量θ的后验分布。在接下来的迭代过程中，作为协变量对其他具有缺失值变量进行回归建模。对于所有含缺失值的变量，重复这个过程，即每次迭代都需要对到进行插补。每次迭代结束时，缺失值都被来自回归模型的预测值代替。描述如等式所示

18、，其中t为迭代周期数，，为t次迭代过程中随机绘制参数，为t次迭代过程中的预估值。观测值在迭代更新过程中不会改变，但在每次迭代中都会更新缺失数据。

19、其中，在步骤3中所述“使用最小二乘法（ols）来计算学生化残差、杠杆、库克距离和dffits来确定异常样本”。采用单一判断进行考察有时并不准确，而往往忽略了对几种方面的综合运用；

20、3-1：杠杆值x空间中的异常值被称为高杠杆点，线性模型表示为，其中x是的观测矩阵，y是的观测向量，b为未知参数向量，e为随机误差向量;

21、使用ols进行回归估计时，可以得到帽子矩阵h，表示为：，很多学者通过帽子矩阵h的对角元素来诊断杠杆点，从而确定可能的影响点，尤其是的点。因此，被用来作为诊断杠杆点的诊断基准。p为特征数量，n为样本数量。可以表示为

22、；

23、3-2：内部学生化残差，使用所有数据拟合得到的回归模型的均方误差，

24、，其中为残差，当的测量误差是独立的并且服从正态分布时，可以得到内部学生化残差；

25、外部学生化残差，使用删除第i次观察值的其它所有数据拟合得到得回归模型得均方误差，

26、，其中是在没有第i次观察值的情况下整个回归运行时的估计值，为外部学生化残差；内部学生化残差从自由度的t分布，外部学生化残差服从自由度为的t分布；学生化残差大约有95.44%的概率落在区间[-2,2]中并且不呈现任何的趋势；若学生化残差超过这个范围，则这些点是异常值；

27、3-3 ：dffits该距离是从数据拟合的观点提出的，考虑第i个点删除前后对处拟合值的影响，定义为

28、，belsley使用的点作为判断异常值的临界值；

29、3-4 ：cook距离是从估计角度提出的一种度量第i个观测点对回归影响大小的统计量，对每个观测点，定义cook距离为：

30、,为观测数据的离差矩阵，为均方误差，n为样本容量。当时，判断其为强影响点。

31、其中，在步骤4中所述“输入训练数据通过k折交叉验证构建的模型进行训练，通过随机搜索和网格搜索算法的组合来选择参数，采用不同的评估标准来评估基础模型性能；”

32、4-1：所述的k折交叉验证为8折交叉验证；

33、4-2： 所述的8折交叉验证策略训练模型步骤如下：首先将训练数据集随机分成8组；依次取出一组数据作为测试集，其余7组数据作为训练集训练一个子模型，得到8个子模型的组合体；组合模型的预报值为4个子模型预报的平均值；

34、4-3： 首先通过随机搜索缩小模型参数的搜索范围，再进一步通过网格化搜索进一步确定最优模型参数；

35、4-4： 使用三个性能指标：

36、，其中，rmse为均方根误差，mae为平均绝对误差和为拟合优度统计量。

37、其中，在步骤5中所述“mic用于计算各基础机器学习模型预测误差相关度，筛选差异较大的基础模型，构建差异最大化的stacking集成模型。”mic不仅可以测量大量数据中变量之间的线性和非线性关系，而且可以广泛地挖掘出响应变量之间的非函数依赖关系。此外，它的计算复杂度低，鲁棒性强。mic越大，特征对响应变量的重要性就越高。可以有效识别差异化大的模型。互信息被定义为：

38、，其中和为两个随机变量，n为样本量。和是x和y的边缘概率分布密度；

39、最大互信息定义为：

40、，其中表示最大互信息值;b为网格划分的上限值,随数据样本数n相关的增长函数,这里筛选模型差异效果最好。为了使构建stacking 模型性能达到最优，在完成各个初级学习器超参数寻优提升学习能力后，还需要进一步考虑各模型之间关联度，选择差异度较大的第1层的基学习器。在保证预测精度的前提下，要尽可能的加入不同种类的预测算法。stacking集成模型构建方式如附图3所示。