一种为卷积神经网络生成图像分类反例的求解方法

本发明涉及深度学习，具体涉及一种为卷积神经网络生成图像分类反例的求解方法。

背景技术：

1、随着计算机硬件性能的不断提升和计算方式的持续创新，卷积神经网络(convolutional neural networks,cnn)经过数十年的不断进化，目前作为一种卓越的具有自学习特征的网络结构已经被广泛应用于图像分类、目标检测等智能识别及决策领域。使用卷积神经网络模型对图像进行分类，当网络模型结构确定后，首先需要借助一个训练样本驱动训练算法如反向传播(back propagation,bp)算法对网络中的权值和偏置量(bias)如卷积核(convolutional kernel)与全连接层(fully connected layer)的权值以及偏置量(bias)进行迭代求精计算，如果权值与偏置量趋于稳定并且网络的拟合输出值与预期值的误差收敛为一个较小的值则训练结束。一般而言，训练后的网络模型的性能如分类准确度及泛化能力的优劣除网络模型的结构及卷积核尺寸等超参数的影响之外，主要由训练样本的质量决定。而训练样本质量与样本数量、样本准确性以及样本覆盖度三个要素密切相关，表现的关系为：样本的数量越多，样本蕴涵的内在规律特征越准确，并且能够覆盖的可能情形越全面，则训练后的网络模型性能越优异，尤其在处理具有相似形态分类对象时其效果越明显。对于样本数量与样本准确性两个要素，由于分类任务明确，通过人工采集、网络搜集以及借助自动生成技术等方式，常常能够构建一个数目众多的、类别鲜明的训练集，并以此可以实现扩展样本数量和提高样本特征规律准确性的目的。然而，相对于样本数量和样本准确性所呈现出的直观可知属性，覆盖度隐含未知属性，通过直观的方法例如提高训练样本数量，常常难以使得覆盖度得到有效提升，本质原因为：训练样本难以涵盖未来可能发生的所有情形，即便使用一个大规模的样本进行训练，训练后的网络模型蕴涵的分类映射关系常常难以区分训练样本之外的所有特征。

2、关于如何提升训练样本质量，一个经验方法为：使用反例(counterexample)图像作为训练样本的一个补充，通过反例的提前展露，能够有效提升样本的覆盖度进而获得更加优质的训练样本。当前，如何获取分类反例图像，已成为解决卷积神经网络在图像分类领域提升分类可靠性及优化性能的核心问题。

3、近年来，随着转置卷积(transposed convolution)及生成对抗网络(generativeadversarial network,gan)等理论方法的不断突破，已有很多自动化图像生成技术被提出并被成功应用于各种图像生成场景如图像还原(image restoration)、风格迁移(styletransfer)等。然而，此类技术借助简单的技术革新都难以胜任自动生成反例样本的任务，原因在于：此类技术经过训练样本学习后，生成的图像与训练样本特征相似且呈正相关性，难以实现生成的图像既要满足目标卷积神经网络模型的分类基线，又要从形态上更具有其他类别特征的要求。实际应用中，对于可靠性要求不高的智能系统，在使用过程中如果遇到识别有误的图像，可以将此图像作为反例样本，通过继续学习的方式进一步地提高模型的性能。然而，如果训练学习后的卷积神经网络模型是在可靠性要求比较高的系统(自动驾驶系统)中承担分类任务，则必须在使用之前对其性能尽可能完成评估以期望达到最优可靠度。为获得最佳性能，常用一个蛮力方法：在分类目标域内，通过人工持续不断地采集样本，尽可能实现反例图像的提前展露，然后一次次地驱动学习，并且反复地迭代整个过程，最终累积出一个较为理想的模型。尽管蛮力法能够有效地提高卷积神经网络模型的可靠性，但此方法需要耗费大量的成本，效率低下。因此，如何设计及实现一种为卷积神经网络模型自动生成反例样本的方法，已成为优化卷积神经网络性能及提高其可靠性亟待解决的问题。

技术实现思路

1、本发明基于可满足性模理论提出一种生成图像分类反例的求解方法，以解决卷积神经网络模型反例样本生成问题。

2、为实现上述目的，本发明采用如下技术方案：

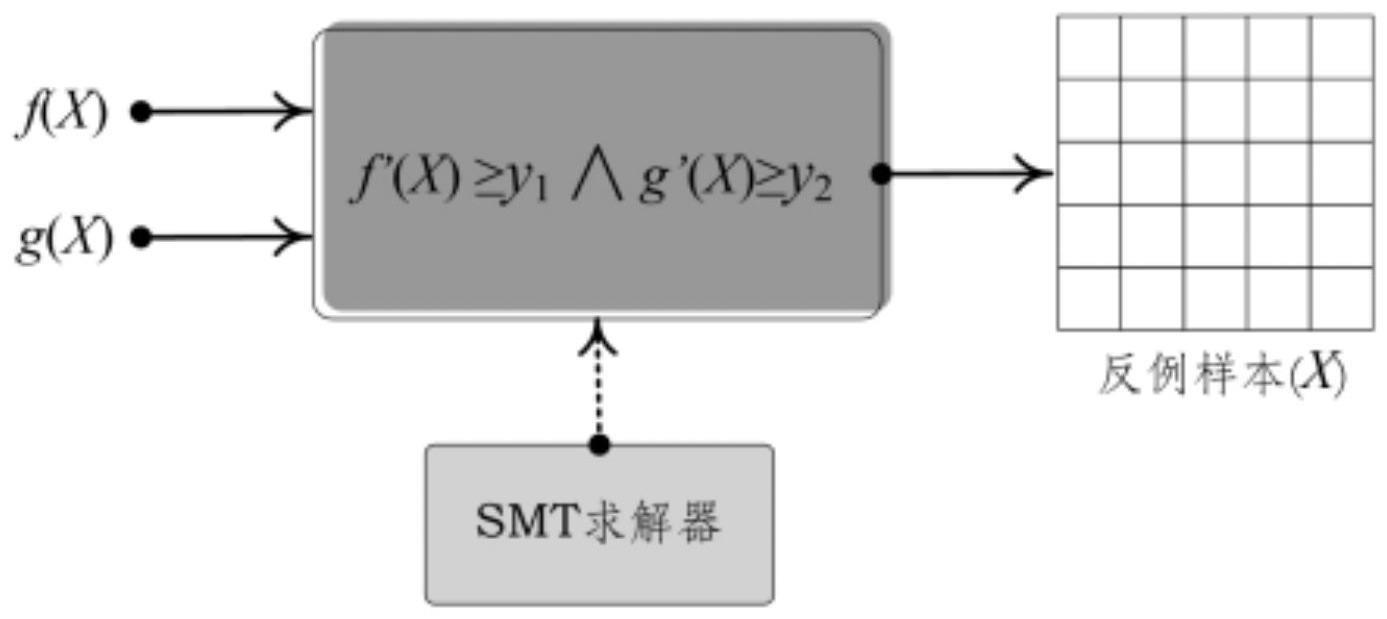
3、一种为卷积神经网络生成图像分类反例的求解方法，首先是将训练后承担分类任务的目标卷积网络模型f(x)转化为等价的可进行满足性求解的模型f’(x)、负责构造反向特征的形态扰动网络模型g(x)转化为等价的可进行满足性求解的模型g’(x)；然后将f’(x)和g’(x)通过逻辑操作符“∧”联立构成一个合取范式形式的求解模型f’(x)≥y1∧g’(x)≥y2，y1与y2为f(x)与g(x)的分类基线，动态设定y1与y2的值控制样本x的形态特征；最后，调用smt求解器对构建的求解模型进行动态推理计算，求解得到的样本x即为反例样本。

4、卷积神经网络模型(cnn)到可满足性求解模型(smt)的转化

5、所述目标卷积网络模型f(x)由输入层(input layer)、卷积层(convolutionallayer)、relu层(rectified linear unit layer)、池化层(pooling layer)、全连接层(fully connected layer)和输出层(output layer)构成。各层计算原理及可满足性模型转化方式论述如下：

6、(1)输入层的模型转换

7、首先将输入图像也即待求反例定义为x，x是基于smt理论定义的以变量为基础构建的一个具有多个通道且不同尺寸的待求解图像，变量的含义为：第k个通道内第i行第j列的像素x；像素x的值在rgb图像模式中为正整数n+且范围为x∈[0,255]，使用转换表达式(1)可对定义的每一个像素变量进行类型及范围的约束，并使用转换表达式(2)完成可满足性模型的归一化转换；例如，对于图2所示卷积神经网络模型，可以用3*6*6个变量表示具有3个通道的尺寸大小为6乘6的一个输入图像，并且使用表达式(2)可完成归一化处理。

8、

9、

10、(2)卷积层的模型转换

11、卷积层的功能是进行特征提取，其输入为待求解反例x，输出为多个特征矩阵d，为了提取到丰富的特征信息，常常使用多个带有偏置量b的卷积核k参与卷积运算，并且卷积核的权值和偏置量在未被训练之前为待求变量，经过训练样本驱动学习后其值得以确定。基于已知卷积神经网络模型的卷积核、步长以及卷积运算方式，通过变量的符号化执行，可将卷积运算转换为可满足性模型。如图2所示，假设卷积核某一个特征提取通道c中的元素c与特征提取通道c感受野对应的图像也即待求反例x的变量x具有对等下标，利用表达式(3)可完成第m个特征矩阵dm的模型转换，其中：为第m个卷积核内第k个通道中第i行第j列的一个已知权值；bm为第m个卷积核的已知偏置量；

12、变量dm为卷积运算后第m个卷积核所对应的特征矩阵dm中的一个元素，由于卷积核权值c∈r，故dm∈r；

13、

14、(3)relu层的模型转换

15、激活函数relu是一种代数非线性斜坡函数，其输入为特征矩阵d，输出为激活特征矩阵r。目标卷积神经网络模型f(x)利用relu函数具有的稀疏特性实现对特征矩阵d中的所有特征元素的非线性激活运算，基于smt理论将relu函数的非线性激活运算转换为一个等价的可满足性逻辑运算表达式。图2所示卷积神经网络的relu函数转换后的可满足性模型见表达式(4)，

16、

17、其中，变量为第m个特征矩阵dm经过relu运算后对应的激活特征矩阵rm中第i行第j列的一个元素，其取值范围为就是第m个卷积核所对应的特征矩阵dm中第i行第j列的一个元素。

18、(4)池化层的模型转换

19、池化计算负责对relu层计算后得到的激活特征矩阵r进行非线性信息过滤，其目的为：在某一区域上指定一个值来代表整个区域，常用的池化操作有最大池化(maxpooling)和平均池化(average pooling)等。如图3所示，假设最大池化运算按照滑动步长执行到某一步，池化窗口所对应的第m个激活特征矩阵rm的四个变量为基于最大池化计算方式，相似于relu转换方式，借助“与”和“非”两种逻辑操作可将某一步的最大池化计算转换为可满足性模型，转换表达式见(5)，其中变量为第m个激活特征矩阵rm经过池化运算后所对应的特征图pm的一个元素，其取值范围为

20、

21、

22、

23、(5)全连接层和输出层的模型转换

24、全连接层的输入为特征图pm所有元素构成的一个一维特征向量v＝[v1,v2,…,vn]，经过综合统筹计算，全连接层输出一个分类值y。全连接层常常具有多层结构，包含多个节点，每一个结点都与上一层的所有结点相连并且指向每一个节点的边都持有一个权值w和一个偏置量b，并且权值w和偏置量b在未被训练之前为待求变量，经过训练样本驱动学习后其值得以确定。分类值y基于全连接层的节点拓扑结构、权值及偏置量可计算得到，某一节点经过多个输入边的汇聚值z的计算表达式见(6)，其中w1,w2,…,wn和b1,b2,…,bn为指向节点的边持有的权值和相应的偏置量。

25、

26、输出层主要负责将全连接层输出的分类值y映射到(0,1)区间内构成概率分布，如图4所示，sigmoid函数常常用于解决二分类概率映射问题，其计算表达式见(7)。相对于sigmoid函数，softmax函数常常用于解决多分类问题的概率映射计算，其计算表达式见(8)。

27、y′＝1/1+e-y                 (7)

28、

29、式(8)中，yj为第j个节点的输出值，k为输出节点个数。

30、全连接层和输出层包含的运算都为算术运算，由于可满足性模理论支持“+”、“–”、“*”、“/”算数运算，基于已知的全连接层网络结构、权值w、偏置量b以及分类概率映射函数，可直接将全连接层和输出层转换为可满足性模型。例如，对于图2所示二分类问题，可直接基于分类值y的表达式和sigmoid函数，将其转化为可满足性求解模型，其中变量y∈r，y’∈(0,1)，sigmoid函数中的e可按照求解精度取一个固定值如e＝2.71作为计算依据。其中，y’是二分类最终计算出来的概率值，y'j是多分类最终计算出来的概率值。

31、smt模型求解

32、基于卷积神经网络模型的计算组件可满足性模型转换方式，可将一个目标网络模型f(x)的所有计算步骤按部就班地转化为等价的可满足性子模型，如果通过逻辑操作符“与”联立这些子模型，可得到一个具有合取范式形式的可满足性求解模型。例如，如果将图2所示卷积神经网络模型的各层的计算步骤转化为可满足性子模型，通过逻辑操作符“与”联立这些子模型，即可获得一个与图3所示网络模型等价的可满足性求解模型。基于获得的目标卷积神经网络模型f(x)的可满足性求解模型，如果设定一个分类基线值如f(x)≥0.8，然后调用可满足性求解器(smt)进行求解，最终可以得到一个满足目标网络模型中所有计算组件为约束条件的样本(图像)x，并且由于relu和最大池化的非线性计算方式，得到的样本(图像)x是众多个可满足性解的空间中的一个特例，其原理与转置卷积技术相同。

33、由于本发明的研究目标为：提出一种求解反例样本的方法，以解决卷积神经网络模型由于训练样本覆盖度不足导致其在分类形态相似对象时性能不稳定的问题。为实现上述目标，反例样本必须满足的属性为：反例样本图像x既要满足目标卷积神经网络模型的分类基线，又要从形态上满足其他类别的特征。依据反例样本必须满足的双重属性要求，一个与f(x)具有相同输入结构但其他结构可以不同并且分类任务互异的卷积神经网络模型g(x)作为形态扰动函数实现反例形态特征的迁移。求解反例样本的具体过程为：首先，分别将目标网络模型f(x)与形态扰动网络模型g(x)转为一个等价的满足性求解的模型f’(x)和g’(x)；然后，将带有分类基线的f’(x)≥y1和g’(x)≥y2通过逻辑操作符“与”联立构成一个合取范式求解模型f’(x)≥y1∧g’(x)≥y2；最后，调用smt求解器yices对求解反例模型f’(x)≥y1∧g’(x)≥y2进行求解，如果yices求得一个高于分类基线的可满足性的解x，则解x为目标卷积神经网络f(x)的一个反例样本，否则证明目标卷积神经网络模型f(x)在给定的形态扰动函数g(x)约束条件内无反例样本，在本发明中形态扰动函数g(x)被认为是一个可靠且可信的网络模型。基于反例求解模型f’(x)≥y1∧g’(x)≥y2，可知分类基线y1与y2蕴含的逻辑关系为：如果固定y1的值，y2的值越大，则反例求解计算受到g(x)的形态扰动越强，生成的样本图像x反例特征越明显。

34、综上，本发明具有如下优点：

35、第一，基于反例模型f’(x)≥y1∧g’(x)≥y2，通过动态调节f(x)和g(x)的分类基线y1和y2的值可自动生成多个反例样本x。例如，固定f(x)的分类基线y1≥0.6并且设定y2的初值为y2＝0.8，如果设定一个步长λ＝0.1逐步提高y2的值y2＝y2+λ，同时不断地调用smt求解器yices对可满足性求解模型f’(x)≥y1∧(y2+λ)≥g’(x)≥y2进行求解可以获得一系列的满足f(x)≥0.6并且g(x)≥0.8的反例样本。

36、第二，本发明的论述过程虽然以图2所示的二分类网络模型为样板，但本发明提出的方法可简单地扩展应用于解决不同结构的卷积神经网络模型，例如具有多分类功能、多层特征提取运算、不同的relu计算方式以池化操作的卷积神经网络模型。