一种基于维纳过程的设备剩余寿命预测方法

本发明涉及设备的剩余寿命预测，尤其是涉及一种基于维纳过程的设备剩余寿命预测方法。

背景技术：

1、目前，在基于年龄和状态相关维纳过程模型的设备剩余寿命预测研究中存在以下的问题：

2、(1)剩余寿命的预测方法普遍针对固定扩散项系数的退化模型。在设备退化的过程中，由于故障的发展可能会导致整个系统的稳定性下降，退化过程的不确定性也会因此增加。如果在退化模型中没有考虑时变扩散项系数将会影响模型的拟合效果和剩余寿命预测的准确性。

3、(2)没有考虑随机阈值。在实际应用中，经常存在失效阈值不明确的情况，如用户需求不同、外部环境影响以及导致失效的具体阈值模糊等。如果剩余寿命预测方法只适用于固定的失效阈值，则会对其实用性造成影响。

技术实现思路

1、本发明的目的是为了在设备剩余寿命预测过程中考虑时变扩散项系数和随机阈值，提高剩余寿命预测的准确性和预测方法的适用性，提供一种基于维纳过程的设备剩余寿命预测方法。

2、本发明的目的可以通过以下技术方案来实现：

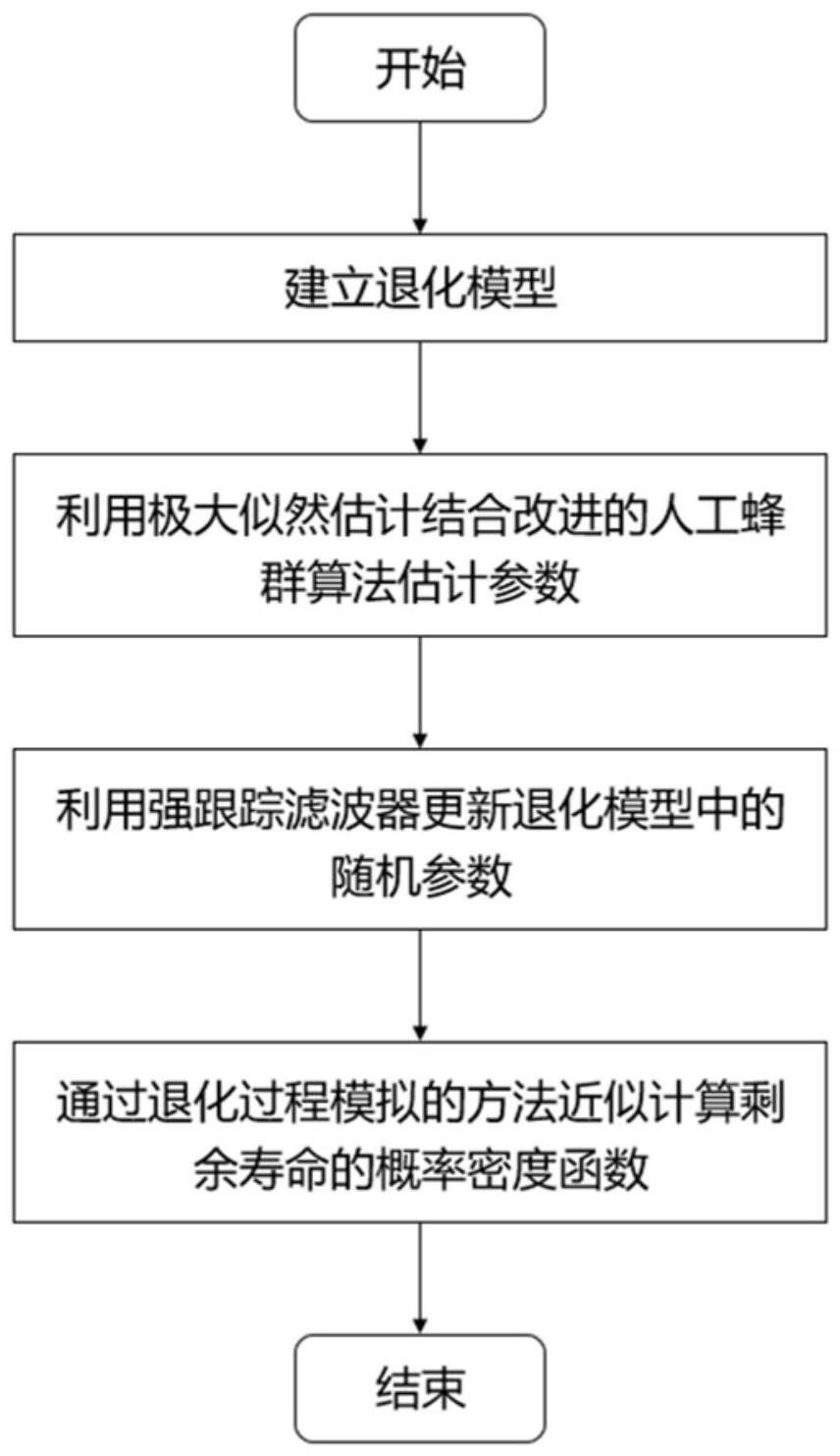
3、一种基于维纳过程的设备剩余寿命预测方法，包括以下步骤：

4、s1、基于年龄和状态相关维纳过程模型，构建退化模型；

5、s2、利用极大似然估计结合改进人工蜂群算法，估计所述退化模型中的参数；

6、s3、利用强跟踪滤波器更新所述退化模型中的随机参数；

7、s4、通过退化过程模拟方法计算设备剩余寿命的概率密度函数。

8、进一步地，步骤s1中，构建退化模型的具体内容包括：

9、基于如下的年龄和状态相关维纳过程模型的一般表达式来构建退化模型：

10、

11、式中，x(t)表示t时刻设备的状态；xk表示设备在初始时刻tk时的状态；为随机参数，用来描述个体间的差异；θ为其他未知参数组成的向量；aλ(x(τ),τ；θ)为漂移项系数函数；σ(τ；θ)为扩散项系数函数；b(τ)为标准的布朗运动。

12、进一步地，步骤s2中，参数估计的具体内容包括：

13、利用欧拉离散的方法对退化模型(1)进行离散化处理。相邻两个观测点之间状态变化量δxn,k-1可以表示为：

14、δxn,k-1＝xn,k-xn,k-1＝aλ(xn,k-1,tn,k-1；θ)δtn,k-1+σ(tn,k-1；θ)b(δtn,k-1)#(2)

15、式中，n＝1,2,…,n，其中n表示退化样本的数量；k＝1,2,…,kn，其中kn表示第n个退化样本中观测点的数量；δtn,k-1＝tn,k-tn,k-1表示两个观测点之间的时间间隔。

16、记δxn＝[xn,1-xn,0,...xn,kn-xn,kn-1]t，根据非线性维纳过程的性质，δxn服从多元正态分布n(μatn,σn)，其中tn的表达式为：

17、

18、

19、式中，tn,k-1＝λ(xn,k-1,tn,k-1；θ)δtn,k-1；dn是一个kn×kn的对角矩阵，其对角线上元素为

20、那么δxn对数似然函数l(μa,σa,θ|x)可以表示为

21、

22、对于式(5)求关于μa的一阶偏导，并令得到μa的估计结果如下：

23、

24、将式(6)代入式(5)，对数似然函数l(μa,σa,θ|x)变为如下的形式：

25、

26、式(7)中含有未知参数σa,θ，这类参数难以通过求偏导数的方法进行估计，下面利用改进的人工蜂群算法进行估计。记v＝[σa,θt]t，具体步骤如下：

27、步骤1：确定每个参数的初始取值范围，并构成一个搜索空间，根据如下的表达式在搜索空间内生成一系列初始的解其中m是初始解的数量。

28、

29、式中，d＝1,2,…,d，其中d是v中参数的数量；r是在区间(0,1)服从均匀分布的随机数；ld和ud分别表示第d个参数的初始取值范围的上界和下界。

30、步骤2：建立如下的搜索机制，寻找新的解

31、

32、式中，s表示参数的随机索引，用来选择在第i次迭代中需要搜索的参数；vbest表示最优解；r1,r2∈{1,2,...,m}，且r1,r2不相等，同时也都不等于m；φ～u(-u,u)，其中u表示扰动幅度；p是一个在区间(0,1)服从均匀分布的随机数，根据p的取值确定搜索策略；sp表示选择概率。

33、步骤3：根据贪婪选择的方法确定需要保留的解。

34、

35、步骤4：依据概率选择需要更新的解，记新解为新解的搜索机制与步骤2中的相同。不同解被选择到的概率如下：

36、

37、式中，fm表示解的适应值。

38、步骤5：设置迭代上限cmax，如果某个解在cmax+1次搜索中都没有在其周围找到更优的解，则舍弃掉它，并根据步骤1的方法再次生成一个新解。

39、将第i次迭代中的最优解作为本次迭代的参数估计结果重复步骤2-5，直到小于预先设置的阈值。

40、进一步地，步骤s3中，参数更新的具体内容包括：

41、步骤1：根据式(3)建立如下状态空间模型：

42、

43、式中，ξ(tk-1)＝σ(tk-1)b(δtk-1)服从正态分布n(0,σ2(tk-1)δtk-1)。

44、步骤2：选择合适的弱化因子β(β≥1)和遗忘因子ρ(0＜ρ≤1)。其中弱化因子一般取一个满足取值范围的经验值，遗忘因子一般取ρ＝0.95。然后计算次优渐消因子：

45、

46、其中

47、

48、

49、

50、

51、步骤3：计算卡尔曼增益：

52、

53、式中，

54、步骤4：更新随机参数的均值和方差：

55、

56、

57、每当有新的观测值产生，通过执行步骤2-4，更新随机参数。

58、进一步地，步骤s4中，剩余寿命估计的具体内容包括：

59、剩余寿命被定义为设备的状态退化首次超过失效阈值的时间，也被称为首次命中时间。根据首次命中时间的定义，设备在tk时的剩余寿命表示为：

60、lk＝inf{l:x(tk+l)≥ω|xk＜ω}#(22)

61、式中，lk表示设备在tk时刻的剩余寿命，inf{·}表示一个变量的下界，ω表示故障阈值。

62、假设失效阈值服从取值范围大于0的截断正态分布剩余寿命的概率密度函数可以表示为：

63、

64、其中，

65、

66、

67、

68、进一步地，利用退化过程模拟的方法近似计算式(23)，具体步骤如下：

69、步骤1：生成一系列服从均匀分布u(μa-3σa,μa+3σa)的离散{an}n＝1:sn，其中sn表示模拟的退化路径的数量。

70、步骤2：设置失效阈值的边界为(μω-3σω,μω+3σω)，根据如下表达式一步一步地生成退化路径，直到退化路径超过失效阈值的上界。

71、xn(li+tk)＝xn(li-1+tk)+anλ(xn(li-1+tk),li-1+tk)δli-1+ri-1#(27)

72、式中，xn(li+tk)表示时刻，第n条退化路径的状态；δli-1是步长；ri-1～u(-ri-1,ri-1)，其中

73、步骤3：将步骤2中的模拟退化路径，代入式(23)中，计算每一个处于失效阈值边界内的观测点所对应的剩余寿命的概率密度。其中，式(25)利用如下的离散形式近似计算。

74、

75、式中，其中p表示观测点所对应的不同剩余寿命的数量。

76、步骤4：整合所有观测点的概率密度：

77、

78、式中，np表示剩余寿命对应的观测点的数量。

79、与现有技术相比，本发明具有以下有益效果：

80、1、本发明能够应用于基于复杂退化模型的设备剩余寿命预测，特别是含有时变扩散项的退化模型，不局限于固定扩散项系数的退化模型，具有更广泛的适用性。

81、2、本发明在设备剩余寿命预测中考虑了随机失效阈值，提高了剩余寿命预测的准确性和预测方法的实用性。

82、3、本发明有利于后续维护计划的制定，提高维护工作的效率并降低成本。