一种求解回转曲面上有界曲面面积的方法

本发明涉及一种求解回转曲面上有界曲面面积的方法，属于回转曲面精密计算。

背景技术：

1、求解回转体上有界曲面面积的情景常见于各种领域。比如化验检测使用研磨钵时残留物会不可避免地在研磨钵壁上粘黏成一个有界曲面，难以清理。当加入新物料时，若研磨钵壁上粘黏的残留物没有清理干净，必然会造成污染，影响检测结果的精度。另外，研磨钵类仪器的清理比较麻烦，现有的方法是将主设备停机，将研磨钵拆除后清理，难以实现自动化。所以根据研磨的物料的情况，我们要实时监测研磨钵的粘黏情况及时进行处理。我们应通过残留物分布的区域面积的大小和黏附物质的成分对检测结果的精度进行综合分析与判断而不是要求工人主观的判断研磨钵是否需要清理。对残留物分布的区域及大小的实时监测就涉及到了求解残留物区域面积的问题，我们可以通过该区域面积大小从而对研磨钵内的污染状况做出定量的分析；在绘制地图时会需要求解某行政区域的面积或者某种植被的覆盖面积，我们可以将这片区域看作地球这个球体上的一个有界曲面，将问题转化为求解这块有界曲面的面积；当对具有回转曲面形状的工艺品进行加工上色等处理时，我们通常需要知道回转曲面上某一区域的加工面积或是上色所需的涂料用量。这时我们可以把问题转化为求解回转曲面上的某区域面积的问题以定量的选择加工的方法及涂料的用量；在以上的情景中，我们希望尽可能准确的求出上述曲面的面积，故亟需一种能够准确而简捷的求解回转曲面上有界曲面面积的方法。

2、随着科学技术的不断发展，出现了多种多样求解回转曲面上有界曲面面积的方法。这些求解有界曲面面积的方法主要分为两种，一种是利用已成熟的软件进行空间有界曲面面积的求解；另一种方法是利用多重积分的思想细分空间有界曲面再进行面积的求和计算。例如，中国专利文献cn102110181a公开了一种自由曲面面积计算方法，该方法包括：边界处理步骤：获取自由曲面的边界点组成的轮廓面，在参数平面内求取逼近该轮廓面的多义线；三角网格化步骤：在参数平面内设置样点，根据设置的样点、所述多义线的顶点以及经过样点的垂直线段或水平线段与多义线的交点构建逼近所述轮廓面的多边形，并对所述多边形进行三角网格化；及计算步骤：根据三角网格化得到的三角形计算自由曲面的面积。又如，西安理工大学乐静等发表的论文“回转曲面上特定区域面积的图像检测方法”，该方法利用透视投影与平行投影的概念，对由于曲面引起的各点物距不同造成的图像变形进行了校正，说明了曲面展开的计算方法，讨论了图像拼接的相关问题。在此基础上，将坐标测量和图像检测技术相结合，通过区域分割拼接的方法提高回转表面上特定区域面积检测的精确度。

3、但是，用软件求取空间有界曲面面积的方法依托于软件内部的功能难以灵活应用于实际；用多重积分求空间有界曲面面积的方法过程繁琐，计算难度大且精度稳定性太差难以应用于对求解结果的速度和精度要求高的场合。

技术实现思路

1、针对现有技术的不足，本发明提供一种更为简便精确且泛用的求取回转曲面上有界曲面面积的方法，即将回转曲面上的有界曲面等面积转换成有界平面再求取其面积。

2、本发明的技术方案如下：

3、一种求解回转曲面上有界曲面面积的方法，包括以下步骤：

4、s1基于周向等长变换原理，将回转曲面上的有界曲面沿周向展开为等面积的有界直纹面；

5、s2再基于等弧长原理，将有界直纹面沿回转轴方向展开为等面积的有界平面；

6、s3基于有界平面的面积计算方法，准确求取回转曲面上有界曲面的面积。

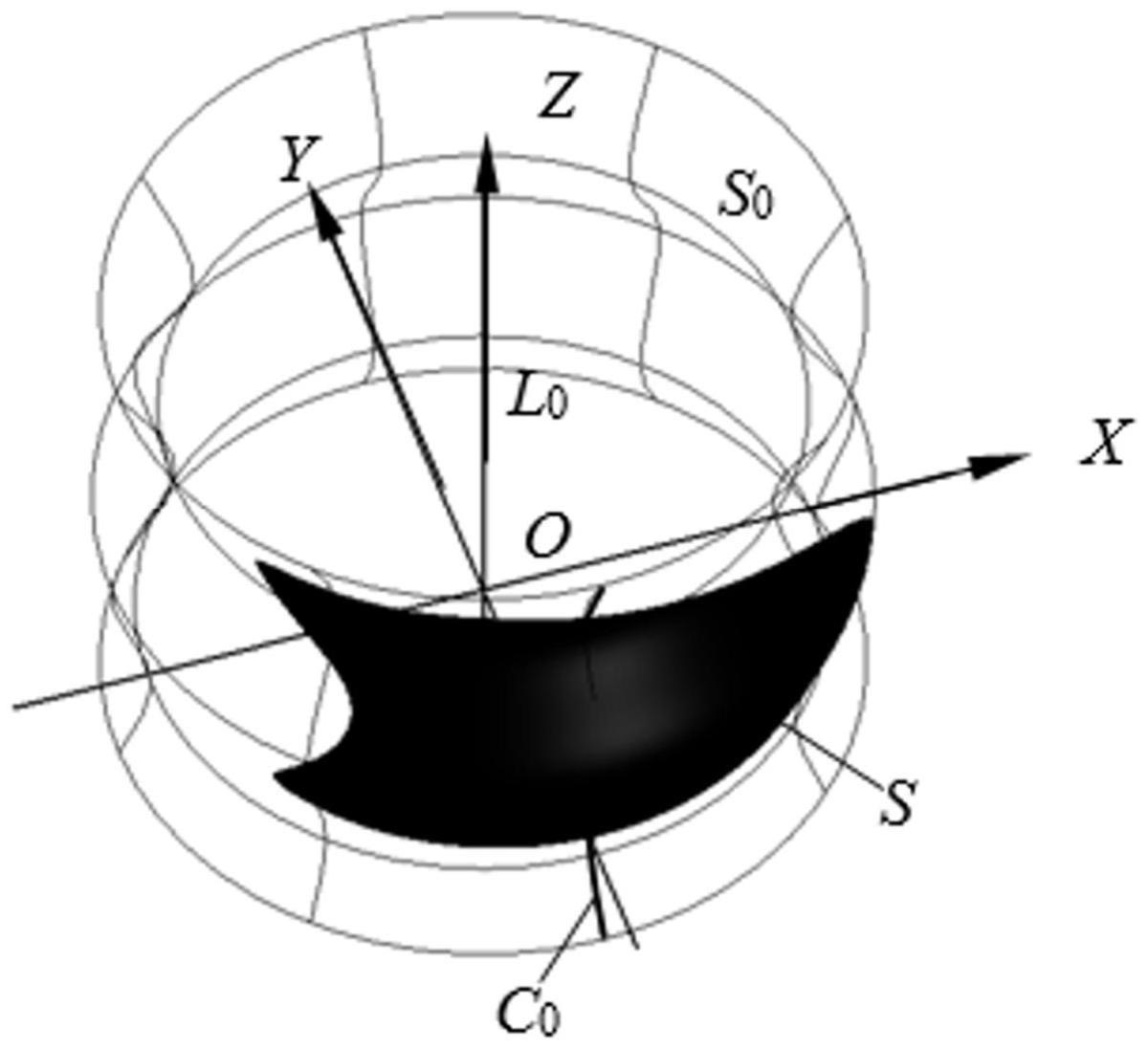
7、优选的，所述步骤s1包括：(1)已知由任意截面曲线c0绕轴线l0旋转形成的回转曲面s0及其上的任意有界曲面s，在轴线l0上任意选取一点o作为坐标原点，沿l0向上的方向作为z轴方向，过原点o垂直于l0且与截面曲线c0相交的直线方向作为y轴的负半轴方向，按照右手定则建立笛卡尔坐标系o-xyz；

8、(2)根据已知的回转曲面上有界曲面s，提取其边界曲线c，选取均分长度s，按照等弧长原则对曲线c均分成n份并取点，得到由n+1个均分点构成的曲线点列pi(xi,yi,zi)(0≤i≤n)，n为自然数；

9、(3)将回转曲面等周向展开，用一张过y轴的正半轴和z轴的剖切面去截回转曲面s0，并将回转曲面上垂直于z轴的任意一个圆，按照等弧长原则分别沿x轴的正向和负向展开为平行于xoz平面的一条线段，从而将回转曲面展开为一张母线平行于平面xoz平面的直纹面s0′，同时原回转曲面上的有界曲面s的边界曲线点列pi(xi,yi,zi)相应地展开为直纹面上的边界点列pi′(x′i,y′i,z′i)，其公式如(1)所示；

10、

11、则由边界点列pi′形成的边界曲线在直纹面上围成一张新的有界直纹面s′；

12、(4)将点列pi′(x′i,y′i,z′i)的各点沿x轴方向投影到截面线c0上形成投影点列qi(xq,yq,zq)，其坐标如式(2)所示；

13、

14、将式(1)代入，qi应表示为：

15、

16、截面线c0是y关于z的函数，用如下公式表示：

17、y＝g(z)                              (4)

18、设截面线c0与y轴负半轴的交点为t0(0,y0,0)，以t0作为曲线c0的弧长起点，则任意投影点qi对在曲线c0上对应的弧长由式(5)求得；

19、

20、优选的，所述步骤s2包括：以直纹面s0′与xoy平面的交线为基准线，将直纹面s0′沿z轴方向展开为一张平行于xoz平面的平面s0″，则s0′上有界直纹面s′的边界曲线点列pi′(x′i,y′i,z′i)相应地展开为平面s0″上的边界曲线点列pi″(x″i,y″i,z″i)，pi″的x坐标与pi′相同；y坐标为定值y0；z坐标的绝对值大小为pi′点在曲线c0上的投影点qi(xq,yq,zq)对应的曲线弧长；pi″坐标如式(6)所示；

21、

22、将式(5)的绝对值符号舍去后代入式(6)，得；

23、

24、优选的，所述步骤s3包括：利用b样条曲线插值原理，将有界点列pi″进行b样条曲线插值，得到一条平面有界参数曲线c′(u)；

25、平面有界参数曲线c′(u)围成了一个新的有界平面s″，s″的面积即为原回转曲面上有界曲面s的面积，通过求解有界平面s″的面积即可获知有界曲面s的面积。

26、优选的，所述步骤(2)中，均分长度s的取值为5mm≤s≤10mm。此设计的好处是，s的大小与边界曲线c形状的复杂程度及计算精度要求有关，常取5mm≤s≤10mm。

27、优选的，所述有界平面s″的面积利用辛普森公式进行数值计算。

28、优选的，当有界曲面s过yoz正半平面时，用一张过y轴的正半轴和z轴的剖切面去截回转曲面s0，则有界曲面s得被截成两张独立的有界曲面s1与s2，分别对有界曲面s1、s2的面积进行求解，然后加和即为原回转曲面上的有界曲面s的面积。

29、本发明的技术特点和有益效果：

30、1、本发明使用了展开变换的思想，将有界曲面通过两次变换，变换为一张有界平面，把相对复杂的对于空间回转曲面上有界曲面面积的求解转换为平面封闭曲域的面积求解，大大降低了求解回转曲面上有界曲面面积的难度。

31、2、本发明所使用的变换方法为等面积变换，最后得到的有界平面s″与初始的有界曲面s的面积完全相同，有效地保证了计算精确。

32、3、本发明方法适用于任意形状回转曲面和回转曲面上任意形状的有界曲面的面积求解，功能完备，适用性强。

33、4、本发明方法是一种互逆变换，不仅可以将空间图形转换为平面图形，也可以将平面图形转换为空间图形，可用于地图制作等领域。