基于加权灰色关联分析法的优选软件可靠性增长模型方法

本发明属于软件可靠性增长模型，具体涉及基于加权灰色关联分析法的优选软件可靠性增长模型方法。

背景技术：

1、为了方便人们的日常需求，人们开发并使用了各种软件。现代社会离不开计算机和人工智能的发展。当计算机中的软件出现故障时，会造成巨大的损失，甚至威胁到人类的生命。在满足软件可靠性运行要求的前提下，不断开发各种软件可靠性增长模型。现代社会中软件实现的功能越来越复杂，代码的规模也越来越大，导致没有一种软件可靠性增长模型能够在所有软件测试环境下准确预测软件中剩余故障的数量，并在所有软件开发和测试环境中有效地估计软件的可靠性程度。

2、考虑到当前的开发和测试环境下，选择最适合当前环境的软件可靠性增长模型是很重要的。研究人员提出了不同的方法来优化软件可靠性模型的选择。例如，ullah等人首先通过比较r2来选择具有最佳拟合性能的模型，然后选择最优软件可靠性增长模型来预测的故障数量和实际检测到的故障数量之间的剩余软件故障数量，该数量小于或等于阈值。sharma等人使用欧几里得复合距离(ecd)来选择最优软件可靠性增长模型。该方法将每个模型的性能指标与最优性能指标进行比较，并计算每个模型与最优备选方案之间的欧几里得复合距离之和。yaghoobi提出使用shannon熵作为srgm的最优选择标准，他还提出使用方差作为标准来优化软件可靠性增长模型的选择。通过比较信息熵、方差和ecd，发现它们之间存在一致性。garg综合熵和距离方法来选择最优软件可靠性增长模型。将该方法与ahp和topsis进行了比较，发现它们的排序方法之间存在相关性。

3、一般来说，统计专业知识是选择最合适的软件可靠性增长模型的首选方法。当已知样本中故障数据集的模式或概率分布时，统计技术在识别最佳软件可靠性增长模型方面是可靠的。然而，在实际的软件测试中，故障检测是不可预测的，并且检测到的故障数量是有限的样本，这在试图发现故障检测的模式和概率分布时带来了很大难度和挑战。因此，使用统计方法选择最佳软件可靠性增长模型受到检测到的故障的实际数量和样本大小的影响。

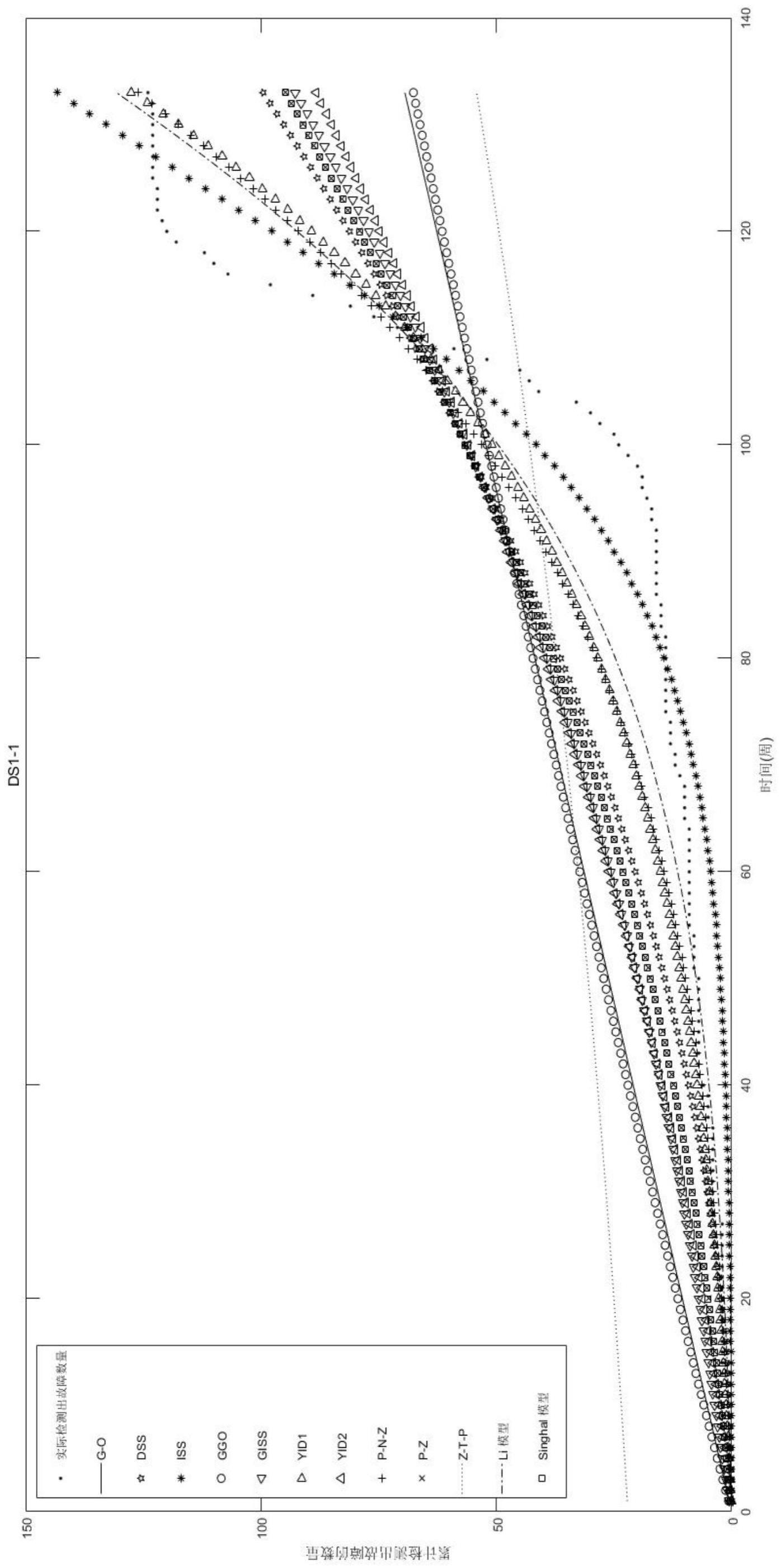
4、由于软件开发和测试的复杂性和不确定性，开发的软件可靠性增长模型只能在某些环境和条件下有效地预测软件中剩余故障的数量，并评估软件的可靠性。例如，在完美调试(pd)环境下，延迟s形(dss)模型假设故障检测曲线随时间呈s形；拐点s形(iss)模型假设它在故障检测过程中存在学习现象，并且检测到的故障的累积数量是随时间变化的s形曲线；goel-okumoto(g-o)模型假设故障检测率是常数；广义goel(ggo)模型假设故障检测服从威布尔分布；一般拐点s形(giss)模型假设故障检测率服从广义拐点s形分布；基于开源软件的li模型假设故障检测率先增加，然后随着测试时间而下降。

5、此外，在不完美调试(id)环境下，yamada不完美调试模型1(yid1)假设故障引入服从指数分布。yamada不完美调试模型2(yid2)假设故障引入显示出随时间的线性变化。p-z模型假设故障引入随时间非线性变化。zhang teng pham(z-t-p)模型假设故障引入率是一个常数，并且s形故障检测率函数随时间非递减地变化。p-n-z模型假设故障检测率不仅随时间呈s形曲线，而且故障引入也随时间线性变化。基于开源软件的singhal模型假设在软件调试期间，故障引入率随着时间的推移表现出不规则的波动，并且故障引入服从指数分布。

6、在软件测试过程中，所收集的故障数据是一个小样本，通常很难确定故障数据的概率分布。故障检测的过程和环境是复杂的、不确定的和动态的。很难将软件可靠性增长模型应用于所有的软件测试环境。在实际的故障检测过程中，检测到的故障数据量波动频繁，甚至表现出突变性。很难找到故障检测的概率分布变化。此外，模型的各种评价标准在评估方面可能有所不同。因此，在当前的软件测试环境中，选择最优的软件可靠性增长模型需要综合考虑各种模型性能评价标准。

技术实现思路

1、本发明针对背景技术中存在的问题，提供了基于加权灰色关联分析法的优选软件可靠性增长模型方法。

2、本发明采用了下列技术方案为：

3、一种基于加权灰色关联分析法的优选软件可靠性增长模型方法，包括以下步骤：

4、步骤1，基于香农熵的权重；

5、利用软件可靠性增长模型的多个评价标准的信息，计算每个软件可靠增长模型评价标准的熵，然后计算权重值，给定具有行m和列n的矩阵z如下：

6、

7、在矩阵z中，每一行表示一个不同的模型，每一列表示用于评估模型的评价标准，矩阵z中有m个软件可靠性增长模型和n个模型的评价标准；zij表示第i个模型和第j个模型评价标准，i＝1,2,...,m和j＝1,2,...,n；基于香农熵的权重计算步骤具体如下：

8、步骤1.1，矩阵z的标准化；

9、如果模型评价标准的值越小，则模型的性能越好，矩阵z的标准化可以表示如下：

10、

11、相反，如果模型评价标准值越大，则其性能越优越，矩阵z的标准化可以表示如下：

12、

13、其中，公式中q1和q2是常量，q1＝0.999999，q2＝0.000001，并且q1+q2＝1；sij表示矩阵z标准化后第i行和第j列，i＝1,2,...,m和j＝1,2,...,n；

14、步骤1.2，计算矩阵z中每个模型评价标准的熵值，公式为：

15、

16、其中，ln表示以e为底对数；

17、步骤1.3，矩阵z中每个模型评价标准的权重，公式为：

18、

19、其中，wj表示矩阵z中第j列模型评价标准的权重；

20、步骤2，加权灰色关联分析方法；

21、根据不同序列曲线几何形状的相似性来确定不同序列模型之间的相关性，加权灰色关联分析方法优选软件可靠性增长模型的具体步骤如下：

22、步骤2.1，等式(1)通过等式(2)或等式(3)进行标准化如下：

23、

24、其中，smn表示标准化后，矩阵sij第m行和第n列；

25、步骤2.2，以矩阵中每列的最小值作为最优评价标准值，如下所示：

26、

27、其中，表示矩阵sij中每列的最小值作为最优评价标准值，上标1,2,...,n表示第几列；

28、步骤2.3，在等式(7)中计算sij和之间每列的距离，公式如下所示：

29、

30、其中，表示矩阵sij中第j列的最优评价标准值，表示矩阵δφij中每列最小值，表示矩阵δφij中每列最大值；

31、步骤2.4，灰色关联系数如下计算：

32、

33、其中，κ表示区分系数，其值为0.5；

34、步骤2.5，基于shannon熵的具有权重的灰色关联度如下所示：

35、

36、其中，ρi表示灰色关联度，其值越高，模型的性能越好。

37、与现有技术相比本发明具有以下优点：

38、1、当软件测试过程中检测到的故障是小样本、数据少和贫信息时，提出的方法可以选择最适合当前软件测试环境的软件可靠性增长模型。

39、2、在软件中检测到的故障数据分布不清楚、模式不明确的情况下，提出优化选择软件可靠性增长模型的方法可以通过数据序列算子的作用来探索故障数据的实际模式。

40、3、提出的优化选择软件可靠性增长模型的方法可以充分利用模型性能的各种评价信息，通过信息熵计算权重优先级，挖掘模型的潜在信息值，为选择最优软件可靠性增长模型做出重要贡献。