一种基于双传感器的时频域欠定盲源分离方法及系统

本发明属于信号处理，具体涉及一种基于双传感器的时频域欠定盲源分离方法及系统。

背景技术：

1、盲源分离技术指在没有任何信号源先验知识或者特定统计信息的情况下从观测信号或混合信号中重建原始信号。欠定盲源分离源的数量大于传感器数量，具有广泛的应用，如无线通信、生物医学信号处理、语音处理、图像处理和模式识别等领域。欠定盲源分离缺乏足够的观测信息，因此目前仍是一个极具挑战的问题。

2、由于自然界中许多信号在时频域为稀疏信号，因此盲源分离算法通常基于源信号的时频稀疏性将混合信号转换到时频域进行处理。现有的欠定盲源分离算法通常可以分为两个步骤：首先利用k-means聚类或基于势函数的聚类等聚类算法估计混合矩阵，然后利用子空间分解或基于追踪算法恢复源信号。然而大部分的欠定盲源分离算法通常限制传感器数目大于两个，并假设时频域自源点上源数目不超过传感器数目，显然这类假设限制了双传感器盲源分离算法的应用。此外，大部分欠定盲源分离算法的性能依赖传感器数目，即当传感器数目较少而源数目较多时，盲源分离算法的混合矩阵估计效果和信号源分离效果都会受到显著的影响。

技术实现思路

1、针对现有的盲源分离方法在源数目较多、时频重叠度较高、传感器数目较少的情况下容易造成混合矩阵估计精度低、源恢复效果差等问题，本发明提供一种基于双传感器的时频域欠定盲源分离方法及系统，能够克服现有盲源分离方法在双传感器设置下的局限性。

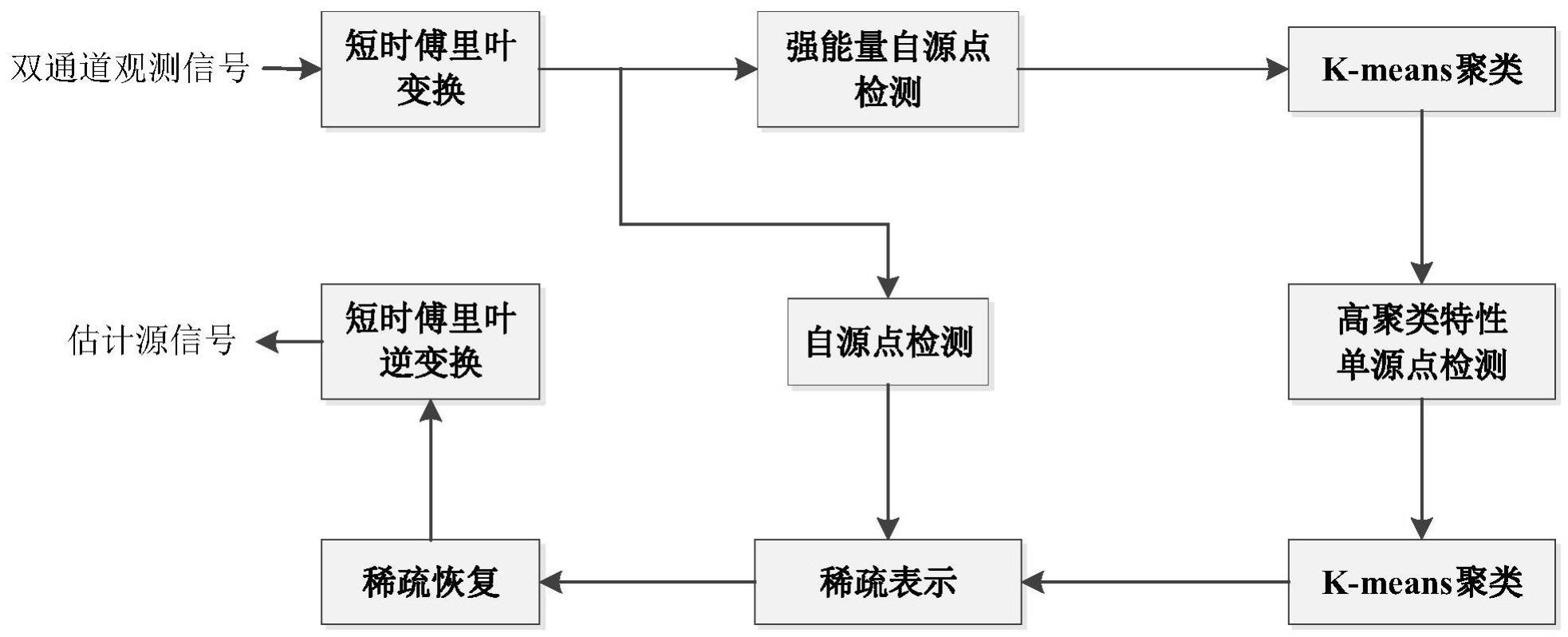
2、为了达到上述目的，本发明提供的技术方案是一种基于双传感器的时频域欠定盲源分离方法，包括以下步骤：

3、步骤1，将双通道观测信号通过短时傅里叶变换转换到时频域；

4、步骤2，从步骤1得到的观测信号时频点中选取强能量自源点；

5、步骤3，对强能量自源点进行聚类，将各个类的聚类中心作为初始估计的方向向量，拼接初始估计的方向向量得到初始空间向量字典；

6、步骤4，使用正交匹配追踪算法从强能量自源点中选出高聚类特性单源点；

7、步骤5，对高聚类特性单源点进行聚类，将聚类中心作为估计混合矩阵的列向量；

8、步骤6，从步骤1得到的观测信号时频点中选取自源点，将自源点集合记为ωasp；

9、步骤7，将自源点集合ωasp和估计混合矩阵进行向量化表示，构建源分离的稀疏恢复模型；

10、步骤8，使用基于l1范数的谱投影梯度下降算法求解稀疏恢复模型；

11、步骤9，将步骤8分离出的时频域源信号进行短时傅里叶逆变换，得到分离的源信号。

12、而且，所述步骤1中基于线性瞬时模型假设，设环境中存在n个源和两个传感器，则传感器阵列接收到的信号可以表示为：

13、x(t)＝as(t)+n(t)   (1)

14、式中，x(t)表示双通道观测信号，s(t)表示待估计的源信号，n(t)表示噪声信号，a表示混合矩阵，t表示时间。

15、使用短时傅里叶变换算法将双通道观测信号从时域转换到时频域，具体计算方式如下：

16、

17、式中，sx(t,f)为经过短时傅里叶变换后观测信号的时频表示，x(τ)表示观测信号的第τ个采样点，h(τ-t)表示汉明窗，e表示自然常数，j表示复数，π表示圆周率，t和f表示时间和频率。

18、而且，所述步骤2中定义观测信号时频域中相对幅度大于阈值t0的点为强能量自源点，强能量自源点集合ωsep表示如下：

19、

20、式中，sx(t,f)为经过短时傅里叶变换后观测信号的时频表示，||sx(t,f)||表示观测信号时频点幅度，表示观测信号时频点中幅度最大的时频点，t0为强能量时频点选取阈值。

21、而且，所述步骤3中根据混合矩阵的性质设置聚类数目n0，并令n0大于源数目n，定义聚类后的聚类中心为初始估计方向向量，对强能量自源点进行聚类的数学表示如下：

22、

23、式中，表示第n个类的聚类中心，也是第n个类的时频点对应的方向向量，表示强能量自源点中第n个聚类的时频点，表示中时频点的数目，t和f表示时间和频率，表示第(t,f)个时频点对应的方向向量，每个子类所有元素的并集为ωsep，即

24、将进行拼接即得初始空间向量字典

25、而且，所述步骤4中使用正交匹配追踪算法对强能量自源点进行第一次分解，具体计算方式如下：

26、

27、式中，表示使表达式取值最小的的取值，||·||表示幅度计算，sx(t,f)为经过短时傅里叶变换后观测信号的时频表示，表示第n个类的聚类中心，表示的moore-penrose伪逆，求解出的方向向量对应该强能量时频点存在第n1个源。

28、对公式(5)分解得到的残余向量再次进行分解，计算强能量时频点去除掉源n1后的残余向量r(1)(t,f)，即：

29、

30、式中，sx(t,f)为经过短时傅里叶变换后观测信号的时频表示，表示第n个类的聚类中心，表示的moore-penrose伪逆。

31、对残余向量r(1)(t,f)进行分解，即：

32、

33、式中，表示求解出的方向向量，表示使表达式取值最小的的取值，||·||表示幅度计算，表示第n个类的聚类中心，表示的moore-penrose伪逆。

34、二次分解求解出的方向向量对应该强能量时频点存在第n2个源，因此sx(t,f)的二次分解可以表示如下：

35、

36、

37、

38、式中，sx(t,f)为经过短时傅里叶变换后观测信号的时频表示，c1表示第n1个源对该强能量时频点的贡献，表示第一次分解求解出的方向向量，c2表示第n2个源对该强能量时频点的贡献，表示第二次分解求解出的方向向量，r(2)(t,f)表示强能量时频点去除掉源n1和源n2后的残余向量，<·,·>表示内积运算，表示的moore-penrose伪逆。

39、利用c1与c2的比值进行高聚类特性单源点判定，即：

40、

41、式中，thcp表示自源点聚类特性，c1表示第n1个源对该强能量时频点的贡献，c2表示第n2个源对该强能量时频点的贡献，sx(t,f)为经过短时傅里叶变换后观测信号的时频表示，表示第一次分解求解出的方向向量，<·,·>表示内积运算，表示的moore-penrose伪逆，表示第二次分解求解出的方向向量，βhcp为设定的阈值。

42、满足公式(11)的时频点即为高聚类单源点，定义高聚类特性单源点集合为ωhcp。

43、而且，所述步骤5中令聚类数目n0等于源数目n，对高聚类特性单源点进行聚类的数学表示如下：

44、

45、式中，表示第n个类的聚类中心，也是第n个类的时频点对应的方向向量，表示高聚类特性单源点中第n个聚类的时频点，表示中时频点数目，t和f表示时间和频率，表示第(t,f)个时频点对应的方向向量，每个子类所有元素的并集为ωhcp，即将进行拼接得到估计混合矩阵

46、而且，所述步骤6中定义观测信号时频域中相对幅度大于阈值t1的点为自源点，具体计算方式如下：

47、

48、式中，ωasp表示自源点集合，sx(t,f)为经过短时傅里叶变换后观测信号的时频表示，||sx(t,f)||表示观测信号时频点幅度，表示观测信号时频点中幅度最大的时频点，t1为自源点选取阈值。

49、而且，所述步骤7中将自源点集合ωasp中的所有时频点组合为一个mnasp×1的向量z，数学表示如下：

50、

51、式中，z为自源点集合向量化表示，m表示传感器数目，nasp表示自源点数目，表示混合信号第m个通道的第nasp个时频点。

52、由估计混合矩阵与单位矩阵计算克罗内克积，数学表示如下：

53、

54、式中，ψ为稀疏观测矩阵，表示克罗内克积，表示形状为nasp×nasp的单位矩阵，δmn表示形状为nasp×nasp的对角线矩阵，其对角线元素等于估计混合矩阵中的元素

55、基于自源点集合向量化表示z和稀疏观测矩阵ψ，构建稀疏恢复模型如下：

56、

57、

58、式中，λ≥0为正则化参数，用于保证解的稀疏性；y表示向量化表示的源信号，表示l2范数，||||1表示l1范数。

59、本发明还提供一种基于双传感器的时频域欠定盲源分离系统，用于实现如上所述的一种基于双传感器的时频域欠定盲源分离方法。

60、而且，包括处理器和存储器，存储器用于存储程序指令，处理器用于调用存储器中的程序指令执行如上所述的一种基于双传感器的时频域欠定盲源分离方法。

61、与现有技术相比，本发明具有如下优点：

62、1)能够同时适用于实数和复数混合矩阵估计；

63、2)基于高聚类单源点估计混合矩阵，在源数目较多、时频混叠严重、观测信号信噪比较低的情况下仍有高精度的混合矩阵估计效果；

64、3)基于自源点稀疏性进行源恢复，可以有效处理自源点上源数目大于传感器数目的情况，打破了传统盲源分离算法对自源点源数目的限制，提高了双传感器欠定盲源分离算法的源恢复效果。