对称翼型附近受限空泡溃灭行为预测方法、系统及设备

本发明涉及流体力学领域，特别是涉及一种对称翼型附近受限空泡溃灭行为预测方法、系统及设备。

背景技术：

1、液体中压力迅速变化时可能导致在压力较低处形成蒸汽或气体构成的小空腔，即空泡。当空泡位于水力机械壁面附近时，气泡溃灭过程中形成的射流会对机械表面材料造成强烈的冲击损伤。对于不同的设备类型和流通位置，壁面的几何形状差异很大，空化所造成的破坏作用也会存在差异。因此，需要研究一种可以有效预测空泡在壁面附近溃灭行为的方法。

2、在流体机械中，曲壁面非常常见，广泛存在于各个过流部件中。当曲壁面位于相当狭窄的液体流动通道时，空化泡会受到狭窄通道的约束，并呈圆柱体形状。柱形泡具有丰富的溃灭动力学特征，与球形气泡明显不同。因此，须建立一个柱形泡在曲壁面附近的动力学模型，以预测空泡的溃灭行为。

3、目前，根据已有的研究，对简单壁附近的空化泡动力学进行了大量的研究，但对复杂曲壁面的研究很少。而翼型作为一个复杂的曲壁面，空泡在其附近的动力学特性将会更加复杂。同时，柱形泡也作为一个新的研究内容，还并没有较为系统地对其进行数学建模以及对溃灭行为的研究。

技术实现思路

1、本发明的目的是提供一种对称翼型附近受限空泡溃灭行为预测方法、系统及设备，可准确预测受限空泡在对称翼型附近的溃灭行为。

2、为实现上述目的，本发明提供了如下方案：

3、一种对称翼型附近受限空泡溃灭行为预测方法，包括：

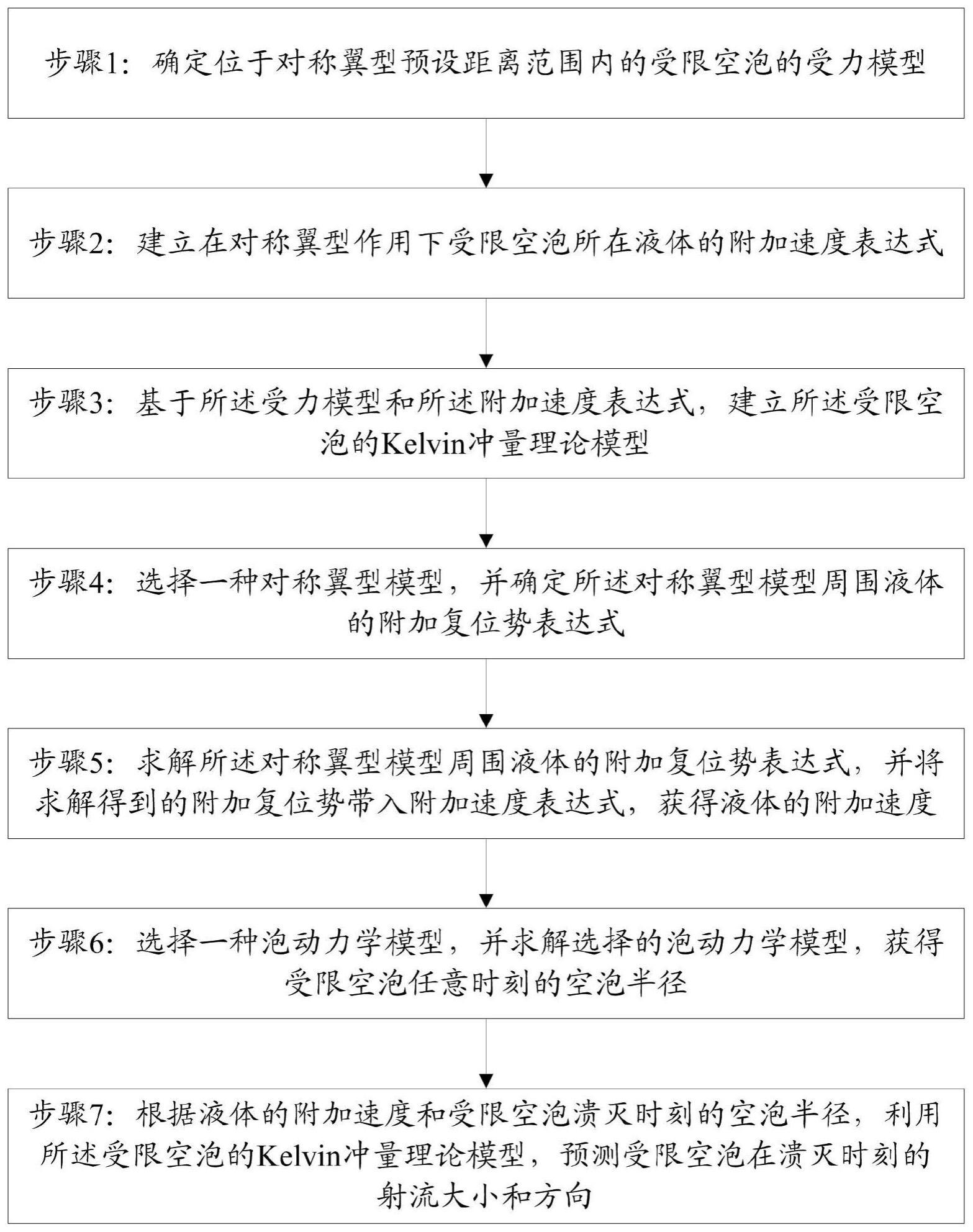
4、确定位于对称翼型预设距离范围内受限空泡的受力模型；

5、建立在对称翼型作用下受限空泡所在液体的附加速度表达式；所述附加速度表达式中的自变量为附加复位势；

6、基于所述受力模型和所述附加速度表达式，建立所述受限空泡的kelvin冲量理论模型；所述kelvin冲量理论模型包括受限空泡的射流大小及方向的模型；

7、选择一种对称翼型模型，并确定所述对称翼型模型周围液体的附加复位势表达式；

8、求解所述对称翼型模型周围液体的附加复位势表达式，并将求解得到的附加复位势带入附加速度表达式，获得液体的附加速度；

9、选择一种泡动力学模型，并求解选择的泡动力学模型，获得受限空泡任意时刻的空泡半径；

10、根据液体的附加速度和受限空泡溃灭时刻的空泡半径，利用所述受限空泡的kelvin冲量理论模型，预测受限空泡在溃灭时刻的射流大小和方向。

11、可选地，确定位于对称翼型预设距离范围内的受限空泡的受力模型，具体包括：

12、确定空泡在对称翼型预设距离范围内所受的力包括浮力以及边界作用于空泡的bjerknes力；

13、基于雷诺传输定理和伯努利方程，确定浮力以及边界作用于空泡的bjerknes力的计算公式为：f′g＝∫sp∞nda＝ρgvey和式中，f′g为空泡所受浮力，f′σ为边界作用于空泡的bjerknes力，s为气泡表面，p∞为流体中的环境压力，n为从气泡壁向内的法向单位向量，da为面积微元，ρ为液体密度，g为重力加速度，v为空泡体积，ey为竖直方向的方向向量，φ为液体速度势，▽为梯度算子；

14、将受限空泡看作一个柱形空泡，并根据柱形体积公式，将空泡所受浮力的计算公式转换得到受限空泡所受浮力的计算公式为：fg＝ρgπhr2ey；式中，fg为受限空泡所受浮力，h为受限空泡的高度，r为受限空泡的瞬时半径；

15、利用lagally定理简化边界作用于空泡的bjerknes力的计算公式，获得边界作用于受限空泡的bjerknes力的计算公式为：式中，fσ为边界作用于受限空泡的bjerknes力，为r对时间的一阶导数，g(s0)为格林函数项，s0为空泡位置坐标；

16、令受限空泡所受浮力的计算公式与边界作用于受限空泡的bjerknes力的计算公式一起构成位于对称翼型预设距离范围内受限空泡的受力模型。

17、可选地，建立在对称翼型作用下受限空泡所在液体的附加速度表达式，具体包括：

18、建立二维势流的复位势表达式为f(z)＝φ+iψ；式中，f(z)为复位势，ψ为液体流函数；

19、将受限空泡看成一个二维点源，在z0点周围的复位势f(z)为：式中，m为点源强度，z0表示受限空泡位于z平面中的z0点；

20、在对称翼型作用下受限空泡所在液体的附加复位势fadd(z)的表达式为：fadd(z)＝f(z)-f(z)；

21、根据所述附加复位势fadd(z)的表达式，建立在对称翼型作用下受限空泡所在液体的附加速度表达式为和式中，uadd为x方向的速度分量，vadd为y方向的速度分量，real[]表示实部，imag[]表示虚部。

22、可选地，基于所述受力模型和所述附加速度表达式，建立对称翼型附近受限空泡的kelvin冲量理论模型，具体包括：

23、根据在对称翼型作用下受限空泡所在液体的附加速度表达式，建立格林函数项g(s0)的表达式为：式中，ex为水平方向的方向向量；

24、根据格林函数项g(s0)的表达式和位于对称翼型预设距离范围内受限空泡的受力模型，确定位于对称翼型预设距离范围内受限空泡的kelvin冲量公式为：

25、

26、

27、

28、式中，i为kelvin冲量，t为一个空泡振荡周期的时间，iσ为bjerknes力作用下的kelvin冲量分量，ig为浮力作用下的kelvin冲量分量；

29、将所述kelvin冲量公式对应的标量模型作为受限空泡的射流大小模型；

30、根据所述kelvin冲量公式，获得受限空泡的射流方向模型为式中，θk为kelvin冲量角度，定义为冲量方向按逆时针方向与x轴正半轴的夹角；ix和iy分别表示kelvin冲量的水平分量和竖直分量，θz为气泡中心与原点的连线和x轴正半轴的夹角。

31、可选地，选择一种对称翼型模型，并确定所述对称翼型模型周围液体的附加复位势表达式，具体包括：

32、选择对称茹科夫斯基翼型模型，并根据圆定理镜像法，确定z平面中对称茹科夫斯基翼型模型周围的点源复位势表达式为：

33、

34、式中，f′(z)为z平面中对称茹科夫斯基翼型模型周围的点源复位势，mr为ζ平面中圆的偏心距离，a为ζ平面中圆的半径，为除了ζ项之外的共轭函数，c为茹科夫斯基变换系数，为z0的共轭函数；

35、基于在对称翼型作用下受限空泡周围液体的附加复位势fadd(z)的表达式，结合z平面中对称茹科夫斯基翼型模型周围的点源复位势表达式，确定对称茹科夫斯基翼型模型周围液体的附加复位势表达式为：

36、

37、式中，f′add(z)为对称茹科夫斯基翼型模型周围液体的附加复位势。

38、可选地，求解选择的泡动力学模型，获得受限空泡溃灭时刻的空泡半径，具体包括：

39、建立选择的泡动力学模型的柱形泡壁运动方程为式中，为r对时间的二阶导数，pr为受限空泡外表面的液体压力；

40、选择在空泡溃灭周期中的溃灭时刻，通过matlab求解所述柱形泡壁运动方程，获得溃灭时刻的空泡半径。

41、一种对称翼型附近受限空泡溃灭行为预测系统，包括：

42、受力模型确定模块，用于确定位于对称翼型预设距离范围内受限空泡的受力模型；

43、附加速度表达式建立模块，用于建立在对称翼型作用下受限空泡所在液体的附加速度表达式；所述附加速度表达式中的自变量为附加复位势；

44、kelvin冲量理论模型建立模块，用于基于所述受力模型和所述附加速度表达式，建立所述受限空泡的kelvin冲量理论模型；所述kelvin冲量理论模型包括受限空泡的射流大小及方向的模型；

45、翼型选择模块，用于选择一种对称翼型模型，并确定所述对称翼型模型周围液体的附加复位势表达式；

46、附加速度求解模块，用于求解所述对称翼型模型周围液体的附加复位势表达式，并将求解得到的附加复位势带入附加速度表达式，获得液体的附加速度；

47、空泡半径求解模块，用于选择一种泡动力学模型，并求解选择的泡动力学模型，获得受限空泡任意时刻的空泡半径；

48、溃灭行为预测模块，用于根据液体的附加速度和受限空泡溃灭时刻的空泡半径，利用所述受限空泡的kelvin冲量理论模型，预测受限空泡在溃灭时刻的射流大小和方向。

49、一种电子设备，包括存储器、处理器以及存储在所述存储器上并可在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现如上述的对称翼型附近受限空泡溃灭行为预测方法。

50、一种计算机可读存储介质，其上存储有计算机程序，所述计算机程序被执行时实现如上述的对称翼型附近受限空泡溃灭行为预测方法。

51、根据本发明提供的具体实施例，本发明公开了以下技术效果：

52、本发明公开一种对称翼型附近受限空泡溃灭行为预测方法、系统及设备，求解选择的泡动力学模型，获得受限空泡任意时刻的空泡半径，可以分析空泡溃灭阶段的泡壁形变；计算对称翼型模型周围液体的附加速度，将附加速度和溃灭时刻的空泡半径带入建立的对称翼型附近受限空泡的kelvin冲量理论模型中，即可预测受限空泡在溃灭时刻的射流大小和方向，实现了受限空泡在对称翼型附近的溃灭行为的准确预测。