基于最小二乘配置的TanDEM-XDEM误差校正方法

本发明涉及一种dem数据的处理方法，尤其涉及一种基于最小二乘配置的tandem-xdem误差校正方法。

背景技术：

1、数字高程模型(digital elevation model，简称dem)是进行各类地学分析的重要基础数据，已被广泛用于水文、地质、气象及军事等各个领域。近年来，随着insar、lidar等航空航天技术的不断发展，获取大尺度全球dem数据的能力日益增强。因此，有着越来越多不同尺度、分辨率、精度的全球数字地面模型公开发布，如aster gdem，alos aw3d30 dem，srtm dem和tandem-x dem等。这些公开的dem为地学相关研究提供了重要的地形参考信息，已经得到了广泛应用。然而这些dem在观测和生成过程中都会不可避免地因为观测技术(如光学、雷达以及摄影测量等)、地形和地表覆盖类型等因素的不同，从而影响所生成的dem数据的精度。例如，基于光学影像立体像对技术生成的aster gdem和alos aw3d30 dem两种dem会因为波长较短，有着难以穿透云雾，易受到噪声、异常值的影响等缺点；同时基于合成孔径雷达干涉成像技术(insar技术)生成的srtm dem和tandem-x dem两种insar dem会因为其观测模式为侧视成像，更加容易受到较大地形倾角的影响，容易在坡度较大的陡峭区域形成数据空洞。

2、德国航空航天中心(the german aerospace center，dlr)在2018年10月公开发布了全球范围的tandem-x dem数据集(90m分辨率)。该数据集是利用雷达卫星干涉测量技术(insar技术)获取，且达到了nga(national geospatial-intelligence agency)规定的hrte-3(high resolution terrain elevation，level-3)规范标准，具有很高的高程精度。当前，tandem-xdem数据集已经在不同地学研究中得到应用，例如冰川变化、矿区勘测和水库蓄水量估算等。但是目前仅向公众开放分辨率为90m，误差范围达8～16米，在山区误差甚至可达近百米。因此，直接影响了tandem-x dem数据的应用潜力和其应用范围。

3、为了充分挖掘公开发布tandem-xdem的应用价值，拓宽它在各领域中的应用，众多学者开展了提升tandem-x dem精度的研究。目前主要从两个方面进行探索，其一是对多源dem进行融合，综合不同观测方式dem的优势，产生比单一dem更加精确、完整和可靠的数据集。例如，岳国栋等人提出了一种升降轨tandem-x dem融合方法，分析升降轨dem存在的问题并将外部辅助dem的方差作为参考进行升降轨dem异常点判别，依据干涉对的相干系数与垂直基线高度加权融合得到最终dem(岳国栋,刘扬,郑春雨.地形复杂区域insar技术的dem融合方法研究[j].测绘与空间地理信息,2021,44(07):205-209.)。其二是根据高精度的点数据与tandem-x dem中对应点的差值，再采用人工智能算法进行训练，从而消除tandem-xdem中的系统误差。例如，kim等人探索了一种利用人工神经网络(ann)改进德国航空航天公司的tandem-xdem(12米分辨率)的方案，该方法使用反向传播算法对网络进行训练，利用代价函数的均方误差最小化目标层与输出层之间的误差(kim d e,liu j,liong s y,etal.satellite dem improvement usingmultispectral imagery andanartificialneural network[j].water,2021,13(11):1551.)。然而这两方面的理论和算法虽然能消除空间大范围呈趋势性的系统误差的影响，但没有考虑高精度点数据对dem随机误差的改善，不能充分发挥高精度点数据对tandem-xdem精度提升的作用。

技术实现思路

1、本发明要解决的技术问题是克服现有技术的不足，提供一种提高tandem-x dem精度的基于最小二乘配置的tandem-xdem误差校正方法。

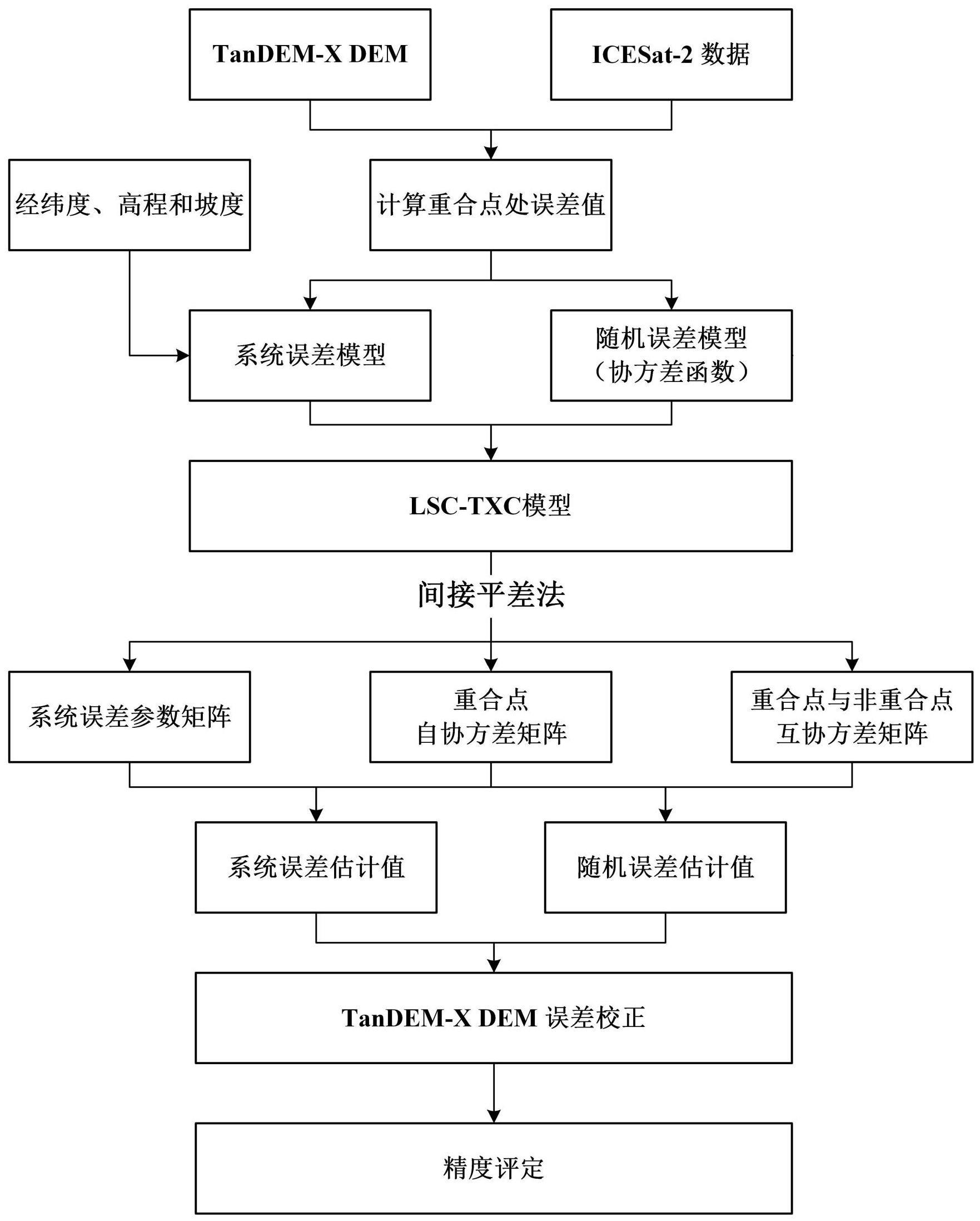
2、为解决上述技术问题，本发明提出的技术方案为：一种基于最小二乘配置的tandem-xdem误差校正方法，包括以下步骤：1)由tandem-x/terrasar-x数据生成tandem-xdem数据，获取icesat-2数据；用栅格数据表示的tandem-x dem数据，每个栅格的值都可以看作是一个点数据的观测值，一个dem数据可以用这个dem面上所有的栅格点数据观测值的集合来表示；

3、将dem数据分为重合点和非重合点，与icesat-2数据重合的这部分栅格点可称为重合点，没有与任何icesat-2数据重合的栅格点可称为非重合点；

4、2)将dem任意一点的误差分为系统误差和随机误差，并建立基于最小二乘配置的tandem-xdem误差校正模型；

5、最小二乘配置的tandem-xdem误差校正模型表示为：

6、l＝bx+gy+δ                    (1)

7、其中，l表示对dem任意一点的误差进行观测获得的观测值，即该点的误差值；

8、b表示系数矩阵，系数矩阵b为m行m列的单位矩阵，m为重合点数量；x为模型的随机误差部分，可以表示为[x'x″]t，其中x'表示重合点处的随机误差，x″表示非重合点处的随机误差；

9、gy表示模型的系统误差部分，其中g是系统误差模型的系数矩阵，y是系统误差模型的参数矩阵；

10、δ为观测噪声；

11、3)由原始的tandem-xdem减去步骤2)得到的误差估计值l，便可得到校正后的dem。

12、本发明中，所述tandem-xdem栅格点误差的随机部分可表示为：

13、lx'＝x'+δ                          (2)

14、lx″＝x″+δ                         (3)

15、与式(1)一起建立最小二乘配置理论的平差模型，即；

16、

17、其中系数矩阵b为m行m列的单位矩阵，m为重合点数量；d'表示重合栅格点的随机误差部分，d″表示非重合栅格点的随机误差部分；tandem-x dem系统误差部分通过与栅格位置、高程和坡度的关联多项式确定，即:

18、

19、y＝[a0 a1 a2 a3 a4 a5 a6 a7 a8]t                 (6)

20、x，y，h，s表示重合点的纵横轴坐标，高程以及坡度。

21、结合式(4)可得，最小二乘配置的tandem-x dem误差校正模型的误差方程：

22、

23、考虑到噪声δ和d'、d″通常是相互独立的，即dδx'＝0，dδx″＝0，dδx'指的是噪声和重合点随机误差的方差，dδx″指的是噪声和非重合点随机误差的方差；根据间接平差原理，公式(7)未知参数的解可通过下式计算：

24、

25、式中，dx'，dδ分别表示x'和δ的方差，dx'x″表示重合点与非重合点的协方差。

26、对式(8)进行化简之后可以得到，tandem-x dem中系统误差部分和随机误差部分的拟合推测估值公式：

27、

28、其中，为系统误差模型未知参数的拟合推估值，和分别为随机误差在重合点和非重合点处的拟合推估值；dx'x'为重合点的自协方差矩阵，dx″x'为重合点和非重合点之间的互协方差矩阵。

29、与现有技术相比，本发明的优点在于：本发明的基于最小二乘配置的tandem-xdem误差校正(lsc-txc)方法，可以同时校正tandem-x dem的系统误差和随机误差。选择欧洲西南部为实验区，实验结果表明，经过本文方法校正后的tandem-x dem在该区域的平均误差绝对值由2.019m减少到了0.058m；均方根误差由6.141m降低到了3.851m，精度提高了37.3％。