一种考虑水作用的系统非平衡演化方法与流程

本发明涉及岩土工程中结构稳定性评价领域，具体涉及一种考虑水作用的系统非平衡演化方法。

背景技术：

1、我国已建及在建的特高拱坝大都处在西南地区，由于河谷快速下切和强褶皱山系的综合作用，西南地区一般具有河谷陡峻、地应力高的复杂地形地质结构及水文地质条件等特点，这就使得坝址区地质体在天然状态下处于临界平衡或者接近临界平衡的状态。剧烈的工程扰动如蓄水等都可能破坏其临界平衡状态，如：锦屏一级和溪洛渡蓄水初期显著的水库诱发地震现象、法国malpasset拱坝蓄水5年后溃坝、意大利vajont拱坝蓄水3年后发生滑坡涌浪等。有必要从非平衡演化的角度对蓄水对结构整体演化的影响进行分析。

2、关于非平衡的演化方法，目前已有的是变形加固理论，核心是最小塑性余能原理，其主要内容是，当确定了外荷载和加载路径时，弹塑性结构总是往塑性余能最小的方向发展即使结构的自承力最大加固力最小。变形加固理论自发展以来，已经运用到岩土工程的各个方面，但该分析过程并未涉及到其它扰动作用如水的影响，即蓄水对最小塑性余能原理的影响。考虑水的作用后，变形加固理论是否适用，最小余能范数的表达式是否成立，需要验证。

技术实现思路

1、本发明的目的在于，克服现有变形加固理论中未考虑水作用的局限性，提供一种考虑水作用的系统非平衡演化方法。

2、为此，本发明的上述目的通过如下技术方案实现：

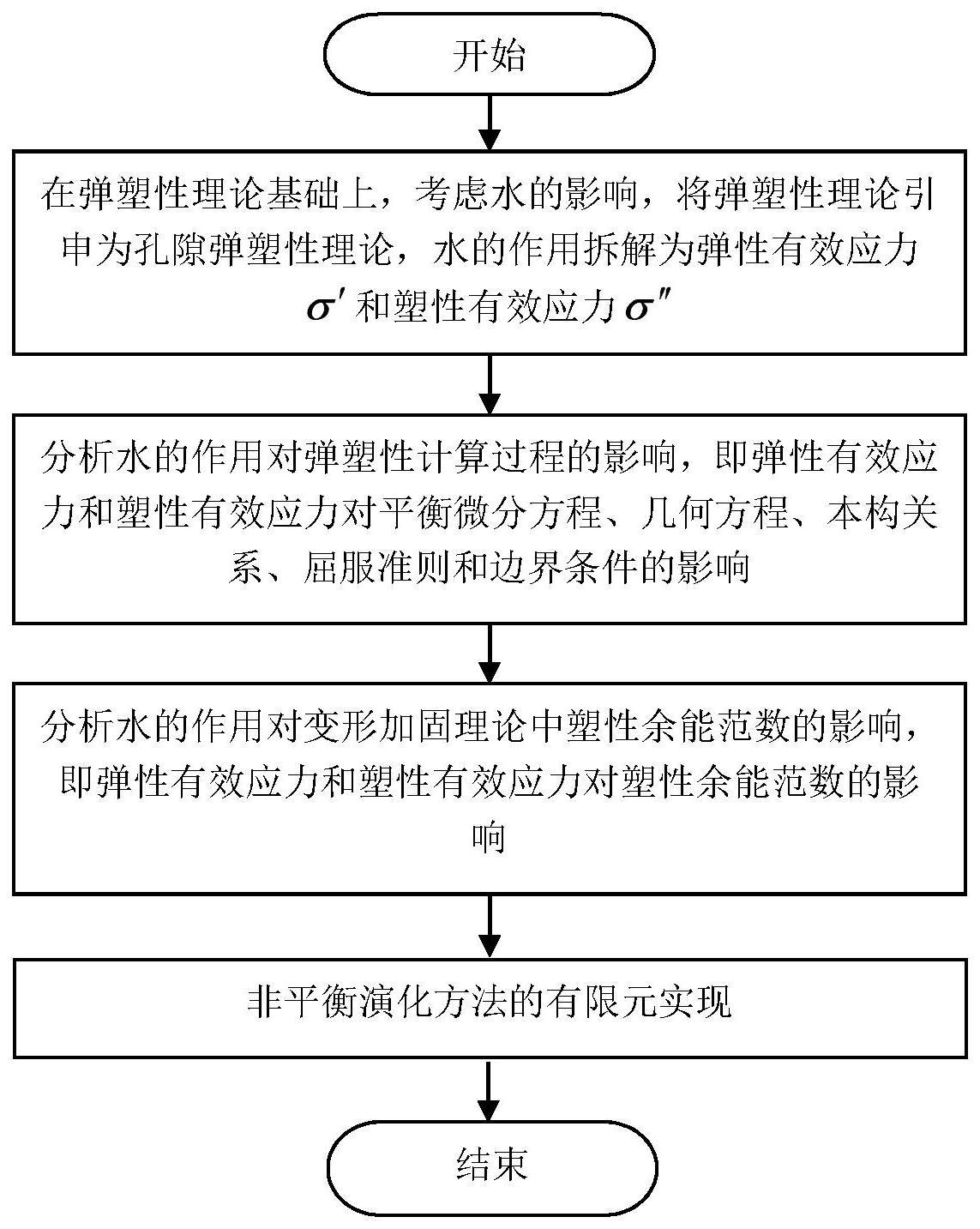
3、一种考虑水作用的系统非平衡演化方法，包括如下步骤：

4、s1、在弹塑性理论基础上，考虑水的影响，将弹塑性理论引申为孔隙弹塑性理论，其中水的作用包括弹性有效应力和塑性有效应力；

5、s2、分析水的作用对弹塑性计算过程的影响，即弹性有效应力和塑性有效应力对三大基本方程和边界条件的影响；

6、s3、分析水的作用对变形加固理论中塑性余能范数的影响，即弹性有效应力和塑性有效应力对塑性余能范数的影响(基于变形加固理论，塑性余能范数是一类推广的lyapunov函数，可用来评价系统的非平衡演化)；

7、s4、将该方法在有限元框架内实现。

8、在采用上述技术方案的同时，本发明还可以采用或者组合采用如下技术方案：

9、作为本发明的一种优选技术方案：步骤s1中，孔隙弹塑性理论，具体为：孔隙介质产生弹性变形的唯一驱动力为弹性有效应力：

10、σ′ij＝σij-αpδij       (1)

11、式中：σij表示分量形式的总应力；σ′ij表示分量形式的弹性有效应力；δij为克罗内克函数；α为弹性有效应力系数即比奥系数；p表示孔隙水压力的大小；

12、孔隙介质产生塑性变形的唯一驱动力为塑性有效应力：

13、σ″ij＝σij-βpδij         (2)

14、式中：σi′j表示分量形式的塑性有效应力；β表示塑性有效应力系数；

15、步骤s2中，分析水的作用对弹塑性计算过程的影响，具体步骤为：

16、s21、给出用分量形式表示的不考虑水的作用时结构的三大控制方程，包括平衡方程、几何方程、本构关系和屈服准则分别如下：

17、

18、

19、

20、

21、式中：fi表示分量形式的体积力；εij表示分量形式的总应变；表示分量形式的弹性应变；表示分量形式的塑性应变；ui表示分量形式的位移；cijkl表示柔度系数张量；f表示屈服函数；

22、s22、给出用分量形式表示的位移边界条件和应力边界条件：

23、

24、式中：表示位移边界上的位移；表示应力边界上的应力；nj表示单位法向量；su表示位移边界；st表示应力边界；位移边界和应力边界要满足su∪st＝s,

25、s23、将有效应力公式σi′j＝σij-αpδij代入平衡方程即(3)，可以推导出用弹性有效应力表达的平衡微分方程和屈服条件为分别：

26、

27、

28、式中：fi表示渗透体积力；弹性有效应力只对平衡方程产生影响，相当于增加了一项渗透体积力，而几何方程、本构方程及屈服条件、边界条件均不发生变化；

29、s24、塑性有效应力只改变屈服状态，具体表现为屈服准则发生变化：

30、

31、式中：f′表示新的屈服函数。

32、作为本发明的一种优选技术方案：步骤s3中，分析水的作用对变形加固理论中塑性余能范数的影响，具体步骤为：

33、s31、给出不考虑水的作用时的黏弹塑性本构关系：

34、

35、式中：和分别为弹性应变率和塑性应变率；

36、duvant-lions模型定义的塑性应变率为：

37、

38、式中：τ是粘滞系数；为经过一段时间最终落在屈服上的应力；

39、s311、根据最大塑性耗散原理：

40、

41、将塑性应变率代入公式(13)，可得：

42、

43、式中：σ是弹塑性计算中屈服面外的一点；是屈服面内或屈服面上的一点；是屈服面上所有点中离σ最近的点；即使下式最小：

44、

45、s312、构造拉格朗日函数：

46、

47、式中：λ为拉格朗日乘子；式(16)在取极值的必要条件为：

48、

49、将塑性应变率代入公式(17)，可得：

50、

51、s313、假设屈服面不随时间变化，即满足一致性条件：

52、

53、将公式(18)代入公式(19)，可得：

54、

55、s32、给出不考虑水的作用时的塑性余能范数：

56、

57、式中：l是两个应力点之间距离的平方在整个结构体积上的积分，衡量了超出屈服面的应力偏离平衡态应力的程度；

58、判断塑性余能范数具备的性质，步骤如下：

59、s321、塑性余能范数一定非负：

60、l≥0(22)

61、式中：当且仅当时，等号成立；此时结构没有超出屈服面的应力，结构平衡且稳定；

62、s322、塑性余能范数的一阶导数为：

63、

64、将塑性应变率(12)、黏弹塑性本构关系(11)和式(20)依次代入公式(23)，可得：

65、

66、式中：第二项非负；第一项可拆分为：

67、

68、将公式(25)代入公式(24)，可得：

69、

70、式中：塑性余能范数的一阶导数恒不大于零，当且仅当时，等号成立；

71、由塑性应变率(12)可知，意味着塑性应变率保持不变，结构将以恒定的塑性应变率一直流动下去，这种状态被称为“极限恒定演化状态”；

72、s323、塑性余能范数的二阶导数为：

73、

74、将黏弹塑性本构关系代入公式(27)，可得：

75、

76、式中：第一项可拆分为：

77、

78、将公式(29)和公式(12)对时间的导数代入公式(28)，可得：

79、

80、式中：被积分式可转换为：

81、

82、将公式(18)对时间求导，并结合公式(19)，可得：

83、

84、将公式(31)、(32)代入公式(30)，可得：

85、

86、式中：塑性余能范数的二阶导数恒不小于零，当且仅当即时，等号成立；

87、s33、弹性有效应力只影响了结构的平衡方程，其对塑性余能范数的影响，具体步骤为：

88、s331、塑性余能范数的定义不变，塑性余能范数的取值仍不小于零l≥0；

89、s332、弹性有效应力对塑性余能范数的一阶导数的影响体现在公式(25)，可得：

90、

91、式中：渗透体积力的时间导数为零，塑性余能范数的一阶导数仍不大于零

92、s333、弹性有效应力对塑性余能范数的二阶导数的影响体现在公式(29)，可得：

93、

94、式中：渗透体积力的时间导数为零，塑性余能范数的二阶导数仍不小于零

95、s34、塑性有效应力只改变了屈服准则，其对塑性余能范数的影响，具体步骤为：

96、s341、塑性余能范数的定义不变，塑性余能范数的取值仍不小于零l≥0；

97、s342、塑性有效应力改变了屈服准则，公式(16)～(19)中的屈服函数统一替换为f′，公式(20)依然成立，塑性余能范数的一阶导数仍不大于零

98、s343、塑性有效应力改变了屈服准则，公式(33)改写为：

99、

100、式中：塑性余能范数的二阶导数仍不小于零

101、作为本发明的一种优选技术方案：步骤s4中，非平衡演化方法的有限元实现，具体步骤为：

102、s41、确实结构荷载及边界条件，其中，荷载包括弹性有效应力等效产生的渗透体积力；

103、s42、计算当前条件下的总应力场，即弹性有效应力场σ′；

104、s43、在弹性有效应力场σ′的基础上，考虑渗透水压力的大小，计算得到塑性有效应力场σ″；

105、s44、将塑性有效应力代入屈服准则：

106、若屈服函数小于等于零，说明结构平衡且稳定，塑性余能范数为零；

107、若屈服函数大于零，更新弹性有效应力进行迭代计算，直到计算收敛，计算此时的塑性余能范数来评价结构的整体稳定性。

108、本发明提供一种考虑水作用的系统非平衡演化方法，在弹塑性理论基础上，考虑水的影响，将水的作用分解为弹性有效应力和塑性有效应力；分析水的作用即弹性有效应力和塑性有效应力对三大基本方程和边界条件的影响，弹性有效应力影响平衡方程，塑性有效应力改变屈服准则；分析水的作用即弹性有效应力和塑性有效应力对塑性余能范数的影响，塑性余能范数的表达式不变，最小塑性余能原理依然成立；将该方法在有限元框架内实现，利用变形加固理论中的塑性余能范数来衡量和评价结构的整体稳定性。本发明所提供的方法克服了现有变形加固理论不考虑水作用的局限性，为分析蓄水扰动问题提供了有效途径。