一种货车线路运输成本预测的方法与流程

本发明涉及物流运输管理与决策支持，具体涉及一种货车线路运输成本预测的方法。

背景技术：

1、根据历史数据或经验公式来估算货车线路运输成本，这种方法简单易用，但是忽略了许多影响因素，预测精度较低。而使用回归法，需要根据货车线路运输成本与各种影响因素之间的数学关系，建立回归模型来预测货车线路运输成本，这种方法可以考虑多个影响因素，但是需要大量的数据和参数，且对数据质量要求较高。然而，以上方法都存在一些不足之处，例如：忽略了货车类型、载重、运输货物品类等对货车线路运输成本的影响；忽略了路线里程、路线类型、天气状态、交通拥堵状态等对货车线路运输成本的影响；忽略了油耗、油价、过路费等动态变化的因素对货车线路运输成本的影响；忽略了货车线路运输成本之间的相关性和时序性。

2、因此，现有的货车线路运输成本预测方法仍有待改进和完善。

技术实现思路

1、本发明的目的是为了解决现有技术中存在的缺点，而提出的一种货车线路运输成本预测的方法。

2、为实现上述目的，本发明采用了如下技术方案：一种货车线路运输成本预测的方法，所述方法具体步骤如下：

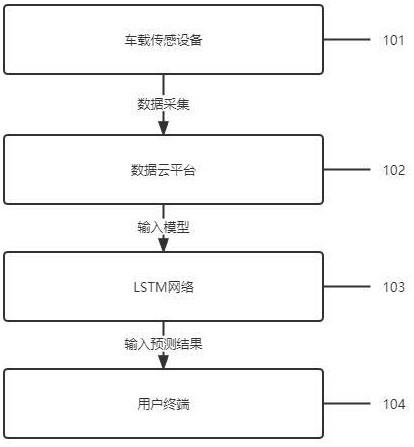
3、s1：数据采集。

4、通过gps定位系统、气象报告、交通报告等，采集货车的运行数据以及货车历史的线路运输成本数据并存储以下数据维度：

5、采集货车的运行数据，包括货车类型、车辆载重、运输货物品类、路线里程、路线类型、天气状态、交通拥堵状态、油耗、油价以及过路费等数据；

6、其中，货车类型为xx款xx牌xx类型的货车；(如：东风天龙牵引车2018款)

7、车辆载重：货车自身的极限的载重；

8、运输货物品类：货车运输的是货物的种类，还包括货物的体积；

9、路线类型：货车从出发地到目的地经过了xx公路、xx高速等；

10、路线里程：货车从出发地到目的地的行驶距离为xx公里；

11、天气状态：货车从出发地到目的地会经过了晴天、阴天、小雨等天气状况；

12、交通拥堵状态：货车从出发地到目的地会经过了畅通、缓行、拥堵等交通状况；

13、油耗：货车每百公里的平均油耗为xx升；

14、油价：货车所加油的地区的油价为xx元/升；

15、过路费：货车所经过的道路的收费标准为xx元/公里。

16、s2：数据预处理。

17、对步骤s1中采集到的货车的运行数据进行预处理操作；

18、所述预处理操作包括数据清洗、归一化以及数据编码；

19、所述数据清洗：将采集到的货车的运行数据进行去除无效、重复、错误、缺失等不符合的数据；

20、归一化：将不同范围和单位的数据转换为统一的标准，如将里程、油耗、油价、过路费等数据归一化到[0,1]区间。

21、进一步的，归一化采用最小-最大缩放处理。

22、最小-最大缩放min-maxscaling：

23、x_scaled＝(x-x_min)/(x_max-x_min)；

24、其中，x表示原始特征的值，x_min和x_max分别表示该特征在整个数据集中的最小值和最大值。

25、缩放后的特征值x_scaled将在0到1之间。

26、数据编码：将非数值型的数据转换为数值型的数据；如将货车类型、运输货物品类、路线类型、天气状态、交通拥堵状态等数据进行独热编码one-hotencoding。

27、s3：特征提取。

28、将步骤s2中预处理后的数据进行特征提取；从预处理后的数据中提取出有效的特征向量；

29、提取出的特征向量为一组包含14为节点的向量组，其中前五位表示货车类型，第六位表示载重，第七位表示运输货物品类，第八位表示路线里程，第九位表示路线类型，第十位表示天气状态，第十一位表示交通拥堵状态，第十二位表示油耗，第十三位表示油价，第十四位表示过路费。

30、s4：模型训练。

31、根据步骤s3中提取出有效的特征向量与货车历史的线路运输成本数据构建一个预测模型。

32、进一步的，所述预测模型具体算法如下：

33、输入门算法：

34、it＝σ(wi·[ht-1，xt]+bi)

35、遗忘门算法：

36、ft＝σ(wf·[ht-1，xt]+bf)

37、细胞状态更新算法：

38、ct＝ft⊙ct-1+it⊙g(wc·|ht-1，xt|+bc)

39、输出门算法：

40、ot＝σ(wo·|ht-1，xt|+bo)

41、细胞状态到隐藏状态的映射：

42、ht＝ot⊙tanh(ct)；

43、其中：t表示当前时间步；w和b是可学习的权重矩阵和偏置项，ht-1表示前一个时间步的隐藏状态，xt是当前时间步的输入；σ表示sigmoid函数，g表示双曲正切函数，⊙表示逐元素相乘。

44、并采用长短期记忆网络(lstm)对预测模型进行训练。

45、进一步的，在将特征向量代入lstm模型进行预测之前，需要进行一些初始化步骤和计算步骤来获取权重矩阵和偏置项，具体的计算过程如下：

46、1)初始化权重矩阵和偏置项：

47、初始化输入门的权重矩阵和偏置项：w_i,u_i,b_i；

48、初始化遗忘门的权重矩阵和偏置项：w_f,u_f,b_f；

49、初始化输出门的权重矩阵和偏置项：w_o,u_o,b_o；

50、初始化隐状态更新的权重矩阵和偏置项：w_c,u_c,b_c；

51、初始化输出层的权重矩阵和偏置项：w_y,b_y；

52、2)计算隐状态和细胞状态的初始值：

53、初始化隐状态：h_0；

54、初始化细胞状态：c_0；

55、3)对于每个时间步t：

56、根据当前时间步的输入特征向量x_t，计算输入门的激活值i_t：

57、i_t＝sigmoid(w_i*x_t+u_i*h_{t-1}+b_i)

58、根据当前时间步的输入特征向量x_t，计算遗忘门的激活值f_t：

59、f_t＝sigmoid(w_f*x_t+u_f*h_{t-1}+b_f)

60、根据当前时间步的输入特征向量x_t，计算输出门的激活值o_t：

61、o_t＝sigmoid(w_o*x_t+u_o*h_{t-1}+b_o)

62、根据当前时间步的输入特征向量x_t，计算候选隐状态的激活值c_t'：

63、c_t'＝tanh(w_c*x_t+u_c*h_{t-1}+b_c)

64、根据输入门、遗忘门和细胞状态更新门的激活值，计算新的细胞状态c_t：

65、c_t＝f_t*c_{t-1}+i_t*c_t'

66、根据输出门和当前细胞状态，计算新的隐状态h_t：

67、h_t＝o_t*tanh(c_t)

68、根据隐状态h_t，计算预测值y_t：

69、y_t＝softmax(w_y*h_t+b_y)

70、s5：模型预测。

71、根据新的特征向量，利用在步骤s4中训练好的预测模型，输出预测的货车线路运输成本。

72、在使用lstm模型进行预测时，输出结果是经过模型计算得出的连续数值。

73、这些数值通常是相对的、归一化的值，代表模型对于某个时间步的货车运输成本的估计；这些值可以通过逆向的归一化处理转换为实际的成本值。

74、逆向归一化的过程是将归一化的数值重新映射回原始的数据范围。常见的方法是根据训练集的最小值和最大值进行逆向转换。具体操作如下：

75、假设训练集的某个数据因子的最小值为min_value，最大值为max_value。

76、对于经过模型预测得到的归一化数值x，可以通过以下公式将其转换为实际的成本值y：

77、y＝x*(max_value-min_value)+min_value

78、通过这样的逆向归一化操作，可以将模型输出的归一化数值转换为实际的成本值。

79、进一步的，通过上述计算步骤，将特征向量x_t代入到lstm模型中，依次计算每个时间步的隐状态和预测值。预测值可以通过softmax函数将输出转化为概率分布；最后，得到的预测值可以用于估计货车运输成本。

80、本模型采用正态分布随机初始化：

81、正态分布随机初始化(normal initialization)：

82、在正态分布随机初始化中，权重矩阵和偏置项的初始值从一个指定的均值和标准差的正态分布中随机抽取。

83、算法步骤：

84、选择正态分布的均值和标准差(例如均值为0，标准差为σ)

85、从该正态分布中随机生成权重矩阵和偏置项的初始值

86、公式表示：

87、初始值＝均值+随机生成的数值*标准差。

88、softmax函数说明：

89、softmax函数是一种常用的激活函数，通常用于多类别分类任务中。它将一组实数转化为概率分布，使得所有输出的概率之和为1。

90、softmax函数的公式如下：

91、

92、其中，zi表示输入向量中的第i个元素，e表示自然对数的底数。

93、该公式首先将输入向量的每个元素zi进行指数化，然后将指数化后的值除以所有元素的指数化和，得到归一化后的概率分布。

94、进一步的，根据损失函数的值，从输出层开始，使用链式法则逐层计算参数的梯度。在lstm模型中，反向传播过程会计算每个时间步的梯度，并根据梯度更新模型中的权重和偏置项。

95、反向传播算法的基本原理是使用链式法则计算损失函数对模型中每个参数的梯度。通过计算梯度，可以确定参数的更新方向，以最小化损失函数。

96、这个过程分为两个步骤：前向传播和反向传播。

97、进一步的，前向传播(forward propagation)：通过将输入数据从输入层经过模型的各个层进行计算，得到最终的输出。在lstm模型中，前向传播过程会计算每个时间步的隐藏状态和细胞状态。

98、具体来说，对于每个时间步t，反向传播的步骤如下：

99、计算输出误差(output error)：根据损失函数和模型的预测输出，计算当前时间步的输出误差。

100、计算梯度(gradient)：使用链式法则计算当前时间步的梯度，包括权重、偏置项和隐藏状态的梯度。

101、传递梯度(backpropagate the gradient)：将梯度从输出层传递到输入层，更新每个时间步的梯度。

102、更新参数(update parameters)：使用梯度下降等优化算法，根据计算得到的梯度更新模型中的参数。

103、这样，通过反复迭代前向传播和反向传播过程，模型的参数会逐步调整，以最小化损失函数。这就是lstm模型训练过程中的反向传播算法。

104、本模型采用均方误差损失函数来比较预测结果与真实值的差异，衡量模型的性能：

105、均方误差损失(mean squared error，mse)：

106、均方误差损失是常用的回归问题的损失函数，其计算公式如下：

107、

108、其中，n是样本数量，y_i是真实值，是模型的预测值。

109、本模型采用随机梯度下降(stochastic gradient descent，sgd)。sgd是一种迭代优化算法，用于更新模型参数以最小化损失函数。

110、进一步的，随机梯度下降算法的基本过程如下：

111、1))初始化模型参数：初始化lstm模型的权重和偏置项。

112、2))迭代训练数据：对于每个训练样本，执行以下步骤：

113、a.前向传播：将输入数据序列通过lstm模型的前向传播过程，计算预测值。

114、b.计算损失：将预测值与真实值进行比较，计算损失函数的值，衡量预测值与真实值之间的差异。

115、c.反向传播：通过反向传播算法计算损失函数对于模型参数的梯度。

116、d.更新参数：根据梯度和学习率的设定，使用梯度下降更新模型参数。

117、下面是随机梯度下降算法的公式表示：

118、前向传播：

119、隐状态更新：

120、输入门：i_t＝sigmoid(w_i*x_t+u_i*h_{t-1}+b_i)

121、遗忘门：f_t＝sigmoid(w_f*x_t+u_f*h_{t-1}+b_f)

122、候选隐状态：c_t'＝tanh(w_c*x_t+u_c*h_{t-1}+b_c)

123、隐状态更新：c_t＝f_t*c_{t-1}+i_t*c_t'

124、输出门：o_t＝sigmoid(w_o*x_t+u_o*h_{t-1}+b_o)

125、隐状态：h_t＝o_t*tanh(c_t)

126、预测值计算：y_t＝w_y*h_t+b_y

127、损失计算：

128、损失函数：l＝sum((y_t-y_t)^2)/n，其中y_t为预测值，y_t为真实值，n为时间步数。

129、反向传播：

130、输出层梯度：dl/dw_y＝(2/n)*sum((y_t-y_t)*h_t)

131、输出层偏置项梯度：dl/db_y＝(2/n)*sum(y_t-y_t)

132、隐状态梯度：dl/dh_t＝dl/dy_t*w_y

133、隐状态更新门梯度：

134、dl/do_t＝dl/dh_t*tanh(c_t)

135、dl/dc_t＝dl/dh_t*o_t*(1-tanh^2(c_t))+dl/dc_{t+1}*f_{t+1}

136、dl/df_t＝dl/dc_t*c_{t-1}

137、dl/di_t＝dl/dc_t*c_t'

138、dl/dc_t'＝dl/dc_t*i_t

139、候选隐状态梯度：dl/dc_t'＝dl/dc_t*i_t*(1-tanh^2(c_t'))

140、输入门梯度：

141、dl/dw_i＝dl/di_t*sigmoid'(w_i*x_t+u_i*h_{t-1}+b_i)*x_t

142、dl/du_i＝dl/di_t*sigmoid'(w_i*x_t+u_i*h_{t-1}+b_i)*h_{t-1}

143、dl/db_i＝dl/di_t*sigmoid'(w_i*x_t+u_i*h_{t-1}+b_i)

144、遗忘门梯度：

145、dl/dw_f＝dl/df_t*sigmoid'(w_f*x_t+u_f*h_{t-1}+b_f)*x_t

146、dl/du_f＝dl/df_t*sigmoid'(w_f*x_t+u_f*h_{t-1}+b_f)*h_{t-1}

147、dl/db_f＝dl/df_t*sigmoid'(w_f*x_t+u_f*h_{t-1}+b_f)

148、输出门梯度：

149、dl/dw_o＝dl/do_t*sigmoid'(w_o*x_t+u_o*h_{t-1}+b_o)*x_t

150、dl/du_o＝dl/do_t*sigmoid'(w_o*x_t+u_o*h_{t-1}+b_o)*h_{t-1}

151、dl/db_o＝dl/do_t*sigmoid'(w_o*x_t+u_o*h_{t-1}+b_o)

152、隐状态更新梯度：

153、dl/dw_c＝dl/dc_t'*tanh'(w_c*x_t+u_c*h_{t-1}+b_c)*x_t

154、dl/du_c＝dl/dc_t'*tanh'(w_c*x_t+u_c*h_{t-1}+b_c)*h_{t-1}

155、dl/db_c＝dl/dc_t'*tanh'(w_c*x_t+u_c*h_{t-1}+b_c)

156、参数更新：

157、学习率：alpha

158、更新参数：

159、w_i＝w_i-alpha*dl/dw_i

160、u_i＝u_i-alpha*dl/du_i

161、b_i＝b_i-alpha*dl/db_i

162、w_f＝w_f-alpha*dl/dw_f

163、u_f＝u_f-alpha*dl/du_f

164、b_f＝b_f-alpha*dl/db_f

165、w_o＝w_o-alpha*dl/dw_o

166、u_o＝u_o-alpha*dl/du_o

167、b_o＝b_o-alpha*dl/db_o

168、w_c＝w_c-alpha*dl/dw_c

169、u_c＝u_c-alpha*dl/du_c

170、b_c＝b_c-alpha*dl/db_c

171、w_y＝w_y-alpha*dl/dw_y

172、b_y＝b_y-alpha*dl/db_y。

173、与现有技术相比，本发明的有益效果为：本发明提供了一种货车线路运输成本预测的方法，通过多维度的数据采集，数据预处理，特征提取，模型训练和模型预测，实现了对货车线路运输成本的实时预测，为物流企业和货车司机提供了一种便捷、高效、智能的决策辅助工具。本发明采用了深度学习算法，如lstm，能够有效地处理时序数据，捕捉数据中的长期依赖关系，并避免梯度消失或爆炸的问题，提高了模型的准确性和稳定性。本发明具有以下优点和创新点：全面地反映货车线路运输的各种影响因素，提高了数据的质量和完整性；有效地处理时序数据，捕捉数据中的长期依赖关系，并避免梯度消失或爆炸的问题，提高了模型的准确性和稳定性；实时地预测货车线路运输成本，为物流企业和货车司机提供了一种便捷、高效、智能的决策辅助工具，有利于降低运输成本，提高运输效率，促进物流行业的发展。