一种基于自适应代理模型的机械结构可靠度计算方法

本发明涉及结构可靠性分析。

背景技术：

1、机械结构可靠性分析的目的是为了度量结构在不确定性因素，如尺寸、载荷、振动及加速度等随机波动下各性能指标的可靠状态。机械结构通常由多个组成装置及关键零部件构成，而各组成装置与其零部件间又彼此影响。在复杂环境-随机载荷交互作用下，其内部关系复杂且充满不确定性，导致失效机理复杂多样，且多失效模式并存，这为准确评估其可靠性增加了难度。此外，在实际工程中，不确定性变量与性能指标间的映射关系很难用解析的物理方程显式表达，即所谓的“黑箱函数”。对于具有黑箱函数的机械结构可靠度计算问题，通常采用调用有限元模型和蒙特卡洛模拟的方式进行计算，该方法虽然能够获得较为满意的分析结果，但计算耗时较长，效率偏低，难以广泛应用。

技术实现思路

1、为了现有技术中机械结构可靠度计算时由于存在多个不确定性变量导致的计算难度大、计算效率低的问题，本发明提供了一种基于自适应代理模型的机械结构可靠度计算方法。

2、本发明为实现上述目的所采用的技术方案是：

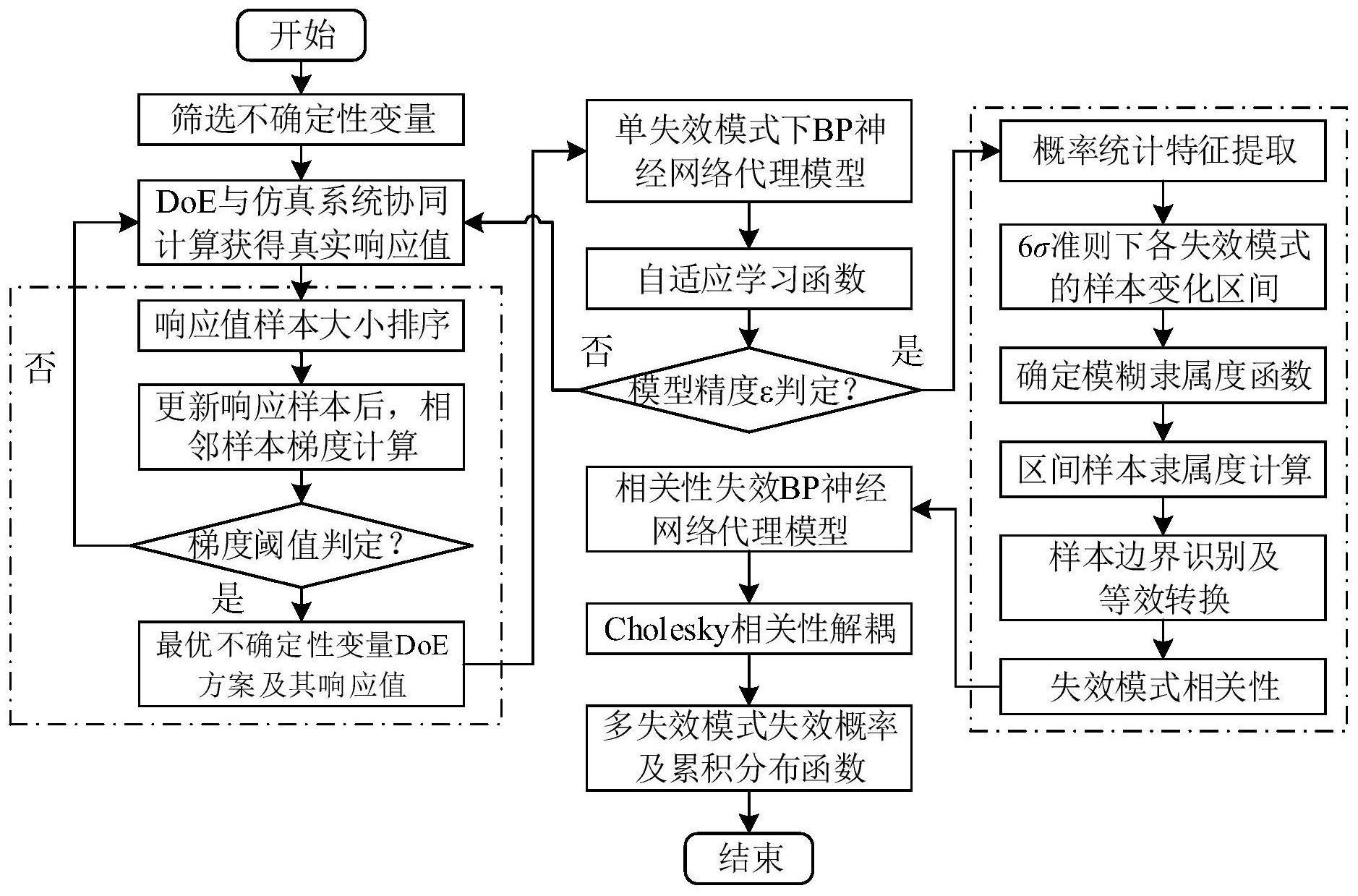
3、一种基于自适应代理模型的机械结构可靠度计算方法，包括以下步骤：

4、s1.确定影响机械结构可靠性的不确定性变量x＝[x1,x2,...xn]，并利用doe方法对不确定性变量进行试验设计；

5、s2.根据不确定性变量的试验设计结果，对机械结构进行参数化仿真分析，获得机械结构失效模式下试验设计对应的响应值y＝[y1，y2，...ym]，并将各响应值样本由大到小进行排序，获得新的样本空间ys＝[y1s，y2s，...yms]；

6、s3.计算新的样本空间中相邻样本点的梯度δyjs，并将计算得到的梯度δyjs与预先设置的梯度阈值比较获得最优的不确定性变量doe试验方案及其响应值；

7、s4.将得到的最优的不确定性变量doe试验方案作为输入层，最优的不确定性变量对应的响应值作为输出层，构建单失效模式下的bp神经网络代理模型；

8、s5.根据单失效模式下的bp神经网络代理模型构建相关性失效下的bp神经网络代理模型及其功能函数；

9、s6.对功能函数进行解耦并计算机械结构在相关性失效模式下的失效概率及累积分布函数。

10、所述步骤s3新的样本空间中相邻样本点的梯度δyjs的计算式如下：

11、δyjs＝yas-ybs

12、式中：yas为新的样本空间ys中的第a个样本点，a＝1，2，3，...m；ybs为新的样本空间ys中的第b个样本点，b＝2，3，...m；

13、将得到的梯度δyjs与预先设置的梯度阈值λ比较，若δyjs≧λ,则ya和yb均进入训练集，若δyjs<λ，则ya进入测试集，yb进入训练集。

14、所述步骤s4构建单失效模式下的bp神经网络代理模型yt的计算式如下：

15、

16、式中：ak与bj为神经元传递阈值；f1(·)与f2(·)为信息传递函数；wkj为权重；vik为速度；i、j、k、n、q为序号，取值为1、2、...m。

17、所述步骤s5根据单失效模式下的bp神经网络代理模型构建相关性失效下的bp神经网络代理模型及其功能函数包括以下步骤：

18、s5-1.利用自适应学习函数z对单失效模式下的bp神经网络代理模型进行更新，使得单失效模式下的bp神经网络代理模型达到模型精度条件ε≥95％；

19、自适应学习函数z的计算式如下：

20、

21、

22、f(x)＝yj-y`j

23、

24、h1(x)＝f′(y`j)

25、h2(x)＝p(y＝y`j)

26、式中：[y]为许用值，yk为样本空间ys中的k个样本点对应的响应值；y`为样本空间ys中的第j个样本点的预测值，yj为样本空间ys中的第j个样本点的试验值；h1(x)为试验响应样本概率密度分布函数；h2(x)为预测响应样本概率密度分布函数；

27、模型精度条件的计算式如下：

28、

29、式中：为试验样本均值；为预测样本均值；

30、s5-2.利用更新后的单失效模式下的bp神经网络代理模型计算机械结构第l个失效模式响应样本的均值和方差sly，计算式如下：

31、

32、

33、式中：ylp为第l个失效模式下的第p个试验响应值，且p＝1，2，...m；ylm为第l个失效模式下第m个样本点对应的响应值；

34、s5-3.利用6σ准则确定各失效模式响应样本变化理论区间[yll,ylu]，以响应样本均值为中心，将失效模式l的样本数据分为上、下半区，分别确定各半区样本模糊隶属度函数识别上半区隶属度最大样本点作为试验区间上限ylla，识别下半区隶属度最大样本点作为试验区间下限ylua；

35、6σ准则下各失效模式样本变化理论区间的计算式如下：

36、yli＝[yll,ylu]

37、

38、

39、式中：yli为第l个失效模式结构响应的区间数理论形式；yll为yli的理论下限；ylu为yli的理论上限；

40、上、下半区的模糊隶属度函数表达式为：

41、

42、式中：d为模糊隶属度函数指数；

43、识别隶属度最大样本点的计算式如下：

44、ylia＝[ylla,ylua]

45、

46、

47、式中：ylia为第l个失效模式结构响应的试验值区间形式；ylla为ylia试验值的下限；ylua为ylia试验值的上限；o为下半区试验样本个数；p为上半区试验样本个数；

48、s5-4.根据所识别的样本边界，对各半区的模糊隶属度函数进行模糊归一化转换，建立理论边界及试验边界转换模型并计算不同失效模式样本点间的夹角θ，量化表征失效模式间的相关性；

49、理论边界和试验边界转换模型的计算式如下：

50、

51、式中：为通过模糊转换得到的第l个失效模式样本边界；为最大模糊隶属度对应的试验样本点，ylwa为第l个失效模式中a样本点对应的响应边界；

52、s5-5.计算不同失效模式样本点间的相关角θ，计算式如下：

53、

54、式中：kmax为试验样本点在二维失效模式坐标系中的最大斜率；kmin为试验样本点在二维失效模式坐标系中的最小斜率；

55、s5-6.根据得到的不同失效模式样本点间的相关角建立相关性失效下的bp神经网络代理模型y′t及其功能函数g，计算式如下：

56、y′t＝g(y1,y1,…yj,θ12,…θij)(i≠j)

57、

58、

59、式中：μi为第i个失效模式均值；μj为第j个失效模式均值；σi为第i个失效模式标准差；σj为第j个失效模式标准差；k为正态分布随机数；θij为第i与第j个失效模式的相关角；[y`j]为第j个失效模式的阈值；y`j为第j个失效模式的实际值。

60、所述步骤s6对功能函数进行解耦，解耦策略计算式如下：

61、ρ＝lu＝llt

62、式中：ρ为两失效模式之间存在的对称且正定的相关系数矩阵；l为下三角矩阵；u为上三角矩阵；

63、计算机械结构在相关性失效模式下的失效概率，计算式如下：

64、

65、

66、式中：mg为ge(x)＜0的个数，m为利用可靠性方法求解时的抽样总数

67、计算机械结构在相关性失效模式下的累积分布函数，计算式如下：

68、z(y′j)＝p（[y`j]＜y`j。

69、本发明与现有技术相比存在的优点是：

70、本发明利用梯度样本筛选准则得到最优的不确定性变量doe试验方案和响应值构建单失效模式下的bp神经网络代理模型，并利用自适应学习函数对单失效模式下的b{神经网络代理模型进行更新，提高了单失效模式下的bp神经网络代理模型的构造精度；同时，构造相关角量化方法，实现了小样本条件下相关性失效的精准量化，并据此构造相关性失效模式下的bp神经网络代理模型，提升了机械结构可靠度计算的准确性和计算效率。