一种基于改进高斯峰值模型的桥梁抗弯刚度分布识别方法

本发明涉及桥梁抗弯刚度分布识别，尤其涉及一种基于改进高斯峰值模型的桥梁抗弯刚度分布识别方法。

背景技术：

1、桥梁是现代交通运输网的重要组成部分，广泛应用于公路、铁路等其他交通方式。随着服役时间的延长，桥梁结构终将进入老化养护期，导致结构性能下降和承载能力降低，引发安全隐患。因此，评估桥梁结构的完整性并确保其安全运行至关重要。桥梁的抗弯刚度与其材料和几何特性密切相关，是桥梁性能的重要指标。有效、准确地识别桥梁实际抗弯刚度分布对评估桥梁健康状态具有重要意义。

2、传统的桥梁刚度退化识别方法一般基于桥梁的动力测试和模态参数识别。该类方法取得了一定进展，但由于其测试一般需要布设大量传感器，且存在对环境变化敏感、对局部刚度退化不敏感的问题。基于桥梁静载试验的方法具有较高信噪比，并对环境变化不敏感，是较为成熟的方法。但是桥梁静载试验以设计荷载加载，并且试验过程需要阻断交通，在经济性和时效性上较为欠缺。最近，学者们提出了一种基于桥梁影响线来评估桥梁抗弯刚度退化情况的方法。与传统方法不同的是，影响线可从桥梁移动载荷试验获取，仅需一个传感器和单辆试验车行驶过桥，成为了近年来刚度退化评估的热门方法。

3、基于影响线进行桥梁抗弯刚度识别时，选择能够合理描述桥梁刚度退化形态的模型是获取准确抗弯刚度分布曲线的关键。现有基于影响线的方法由于并未结合合适的抗弯刚度退化模型，其识别的分布曲线存在波动较大和精度较低等不足。桥梁抗弯刚度退化形态通常具有峰值点并且存在一定影响范围，抗弯刚度会随着远离峰值点逐渐减小。针对这种情况，传统的均匀折减模型难以适用。亦有学者提出了三角形和近似三角形折减模型来描述裂缝引起的抗弯刚度退化。这些模型使用与裂纹深度相关的形函数来表示裂缝附近抗弯刚度变化，可有效描述单个裂缝。然而，三角形和近似三角形折减模型假定抗弯刚度退化为尖端形态，其并不能准确表示裂缝群。实际上，桥梁裂缝区域通常由一条主裂缝和若干辅裂缝组成。因此，抗弯刚度退化的分布形态并不是理想的均匀折减或是尖端形态，更多情况呈现出介于两者之间的形态。目前，鲜有刚度分布识别方法结合较为合理的刚度退化模型，在识别准确的桥梁刚度分布曲线上存在困难。

技术实现思路

1、为克服上述问题，本发明提出一种改进的高斯峰值模型描述桥梁刚度退化分布，并采用levenberg-marquardt(lm)优化算法从桥梁影响线中识别模型参数，实现桥梁抗弯刚度分布识别。

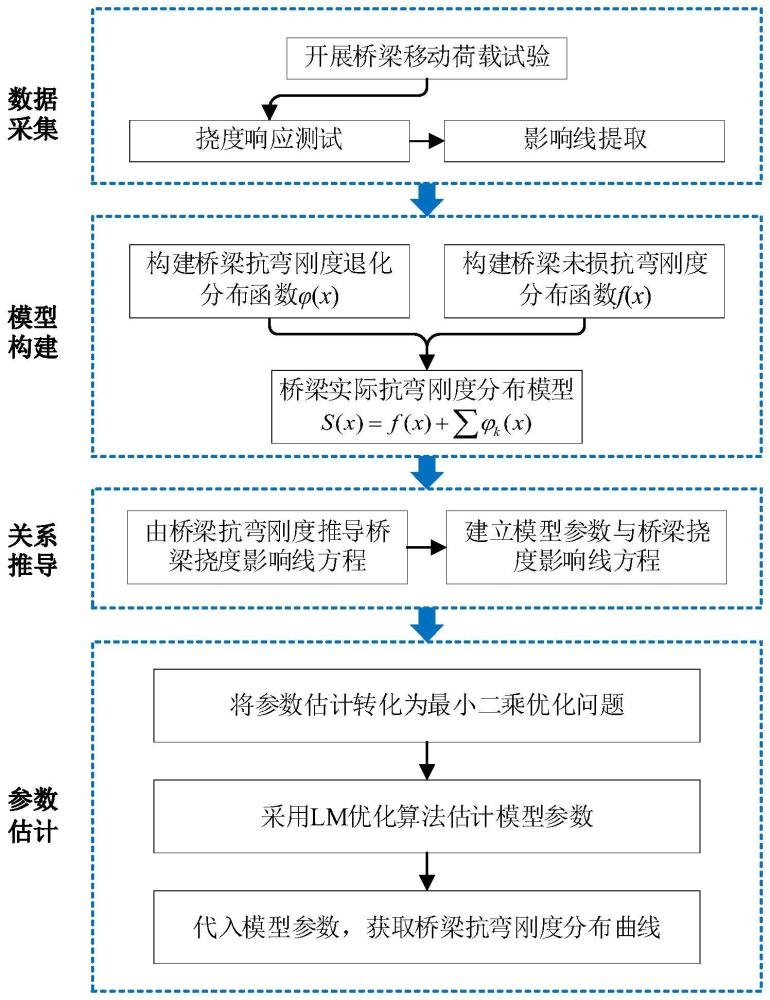
2、本发明采用的技术方案是：一种基于改进高斯峰值模型的桥梁抗弯刚度分布识别方法，包括以下步骤：

3、a.从桥梁移动荷载试验中获取实际挠度影响线；

4、b.构建描述桥梁实际抗弯刚度分布的函数模型；

5、c.建立桥梁抗弯刚度与桥梁挠度影响线的关系；

6、d.采用levenberg-marquardt优化算法，即lm优化算法，从桥梁挠度影响线中识别改进高斯峰值模型的参数。

7、进一步，所述步骤a具体包括：

8、a1.开展桥梁移动荷载试验，测试桥梁挠度响应；

9、a2.从桥梁移动荷载响应中提取桥梁实际影响线，作为识别桥梁抗弯刚度的基础数据。

10、进一步，所述步骤b具体包括：

11、b1.采用改进高斯峰值函数描述由局部损伤导致的抗弯刚度退化，并根据桥梁截面特征选取未损状态下的桥梁抗弯刚度分布函数；

12、桥梁抗弯刚度退化模型采用改进高斯峰值函数，表示为：

13、

14、其中，a表示曲线的峰值，该峰值与损伤程度相对应；b表示峰值中心的位置，峰值中心的位置代表损伤位置；c控制损伤的影响范围；r控制峰值两侧曲线的斜率；

15、未损桥梁的函数模型f(x)采用多项式描述；对于等截面梁，未损抗弯刚度分布是恒定的，表示为f(x)＝d；对于变截面梁，表示为二次曲线f(x)＝ax2+bx+c；

16、b2.构建桥梁实际抗弯刚度分布模型，包括未损状态下的桥梁抗弯刚度分布和由局部损伤导致的抗弯刚度退化，表示为：

17、

18、其中，s(x)表示桥梁实际抗弯刚度分布函数；f(x)表示未损桥梁的抗弯刚度分布；表示第k处局部损伤导致的桥梁抗弯刚度退化；

19、结合改进高斯峰值函数和多项式函数，桥梁的实际抗弯刚度分布表示为：

20、

21、其中，p,q,d为多项式系数；ak,bk,ck,rk为描述第k处损伤的改进高斯峰值函数的参数。

22、进一步，所述步骤c具体包括：

23、c1.根据桥梁抗弯刚度，推导一般桥梁结构的挠度影响线；数值运算中，挠度影响线表示为矩阵形式：

24、d＝dx mmp e＝ne                      (4)

25、其中，d是影响线向量；m是m(x，x)的离散矩阵；mp是mp(x)离散的对角矩阵；e是与桥梁抗弯刚度相关的向量；n是抗弯刚度与挠度影响线的变换矩阵；

26、c2.引入改进高斯峰值模型，建立模型参数与桥梁挠度影响线方程；改进高斯峰值模参数与桥梁挠度影响线的关系方程表示为：

27、d＝ne(p,q,d,ak,bk,ck,rk) (5)

28、其中，向量e包含拟待估计的参数y＝[p,q,d,ak,bk,ck,rk]，其理论方程表示为：

29、

30、其中，e(x)是与抗弯刚度分布相关的函数，p,q,d为多项式系数；ak,bk,ck,rk为改进高斯峰值函数的参数。

31、进一步，所述步骤d具体包括：

32、d1.根据模型参数与桥梁挠度影响线方程，建立最小二乘优化问题；找到最佳参数，使预测影响线与实际影响线达到最佳吻合；以实际影响线为目标值向量，预测影响线为与改进高斯峰函数相关的输出向量，表示为最小二乘优化问题：

33、

34、其中，为2范数；r(y)为残差；f(y)＝dp(y)-da；dp(y)和da分别为预测影响线和实际影响线；δy是增量步长；j是f(y)的雅可比矩阵；

35、d2.采用lm优化算法实现模型参数估计，该优化算法获得的最优解为：

36、

37、其中，i为单位矩阵，λ为控制系数，f(y)和相应的雅可比矩阵j表示为：

38、

39、d3.代入模型参数，获取桥梁抗弯刚度分布曲线。

40、本发明的有益效果是：

41、(1)改进高斯峰值模型为桥梁的刚度退化分布提供了更全面和准确的表示。通过引入额外参数，该模型有更广泛的变化范围，能够有效地描述多种复杂的损伤形式。改进高斯峰值模型不仅能够包含既有的模型(均匀、三角形和近似三角形折减模型)，而且弥补了它们的局限性，提供了一种更为通用的刚度退化描述方法。

42、(2)利用lm算法可有效估计改进高斯峰值模型中的参数，使其与桥梁实际抗弯刚度分布吻合。这种优化算法可有效避免计算中矩阵奇异的情况，对噪声以及干扰信息不敏感。该方法获取的抗弯刚度分布曲线具有较高准确性，可更为直观的反应桥梁实际健康状态。

43、(3)本方法可从桥梁挠度影响线中识别桥梁的抗弯刚度。相比传统方法，桥梁挠度影响线可通过桥梁移动荷载试验获取，仅需单个测点和单辆测试车行驶过桥，在经济性和时效性上具有明显优势。