一种基于概率框架和Kriging代理模型的加工颤振稳定性预测方法与流程

本发明涉及数控加工制造，具体涉及一种基于概率框架和kriging代理模型的加工颤振稳定性预测方法。

背景技术：

1、在数控加工过程中，极值化的加工参数设置虽然可以提升生产效率，但同时也更容易引起刀具振动甚至加工颤振，造成生产质量下降甚至刀具损坏等不良后果。加工颤振稳定性分析理论和技术可以指导工程师合理选择加工参数，对于提高数控加工生产效率与质量具有至关重要的作用。

2、数学上来说，加工颤振稳定性分析是通过对铣削过程进行数学物理建模，利用微分方程定性理论知识判断给定加工参数下的系统稳定性状态，最终得到铣削稳定性叶瓣图(stabilitylobediagram，sld)。然而，现有稳定性分析方法(如全离散法，fdm)预测得到的稳定性叶瓣图与真实切削实验中的稳定性边界仍存在较大差异，这主要是因为：1.作为铣削动力学方程输入的模态参数受到测量误差，模型简化等一系列因素影响，存在“测不准”现象；2.真实切削过程中，模态参数会随着加工状态、加工策略的改变而变化，但在传统方法中，模态参数往往是在静态实验下测量拟合得到。

3、针对目前加工颤振稳定性分析方法所面临的问题，一方面，需要针对模态参数的不确定性给出精确度量；另一方面，需要对部分模态参数随加工状态的变化给出动态建模。

技术实现思路

1、为解决上述技术问题，本发明中提供了一种基于概率框架和kriging代理模型的加工颤振稳定性预测方法，通过构建并优化模态参数分布，基于概率框架给出针对参数不确定性的精确度量；通过拟合模态参数随主轴转速变换的函数关系，并利用kriging代理模型预测动态模态参数下的稳定性叶瓣图，利用预测均方误差生成鲁棒性更强的稳定性叶瓣图下边界，最终得到高转速区域下鲁棒性更强，精确度更高的稳定性叶瓣图。

2、为解决上述技术问题，本发明采用如下技术方案：

3、设计一种基于概率框架和kriging代理模型的加工颤振稳定性预测方法，包括下列步骤：

4、s1、构建模态参数联合分布：首先确定铣削系统中的模态参数种类，建立系统模态参数的独立联合正态分布，利用平均切削力模型拟合的切削力系数与多次冲击实验测量出的动力学参数平均值作为联合分布的均值，根据动模态分析结果适当选择联合分布的方差；

5、s2、利用全离散法构建kriging代理模型训练集：从步骤s1中得到的联合分布中采样若干组带有不确定性的模态参数，并利用传统离散稳定性分析方法计算得到这组采样结果下kriging代理模型的训练集；

6、s3、使用matlabtoolboxdace训练kriging代理模型：通过利用训练后的kriging代理模型预测出动模态参数上鲁棒性更好、精确度更高的稳定性叶瓣图；

7、s4、在动态模态参数上利用kriging代理模型预测加工稳定性：通过参考对模态参数的灵敏度分析结果，在选择kriging相关模型系数上下界时，通过对不同重要程度的参数设置不同的相关模型系数变化范围，实现了对模型不确定性的更准确度量。

8、优选的，步骤s1中：对于2个自由度的铣削系统，带有不确定性的模态参数选择为i＝x/y方向上的刚度ki(n/m)、阻尼比ζi(％)、固有频率ωni(rad/s)以及轴向/径向切削力系数ktc/krc(mpa)；此时所有模态参数构成向量w∈r8；构建模态参数向量w的独立联合正态分布μw为正态分布均值，∑w为正态分布协方差矩阵：

9、w＝[ωnx，ωny，ζx，ζy，kx，ky，ktc，krc]t#(1)

10、

11、

12、s11、选择正态分布均值：其中刚度、阻尼比和固有频率的均值选择为多次结构动力学冲击实验测量结果的平均值，切削力系数的均值选择为平均切削力模型中满足最小二乘回归的拟合值；

13、s12、选择正态分布方差：初始模态参数的方差统一选择为均值的10％，后续可根据预测结果进行调整。

14、优选的，所述步骤s2中，构建kriging代理模型训练集的具体方法为：

15、s21、选择待预测稳定性叶瓣图主轴转速(spindle speed，ss)上下界ssmax，ssmin；选择待预测稳定性叶瓣图切削深度(depth of cut，dc)上下界dcmax，dcmin；此时待预测加工参数区域为

16、{(ss，dc)|ss∈[ssmin，ssmax](rpm)，dc∈[dcmin，dcmax](mm)}；

17、选择正整数m和n，将加工参数空间均分成(m+1)×(n+1)的网格：

18、

19、加工参数网格将用于后续全离散法计算；

20、s22、选择正整数n，从模态分布联合分布中采样n组模态参数对于加工参数格点(ssi，dcj)，使用全离散法计算对应全体的所有转移矩阵谱半径最终得到作为加工参数网格格点(ssi，dcj)处的训练集，用于训练kriging代理模型；遍历所有加工参数格点，得到全体训练集

21、优选的，所述步骤s3中训练kriging代理模型的方法为：

22、s31、选择dace库中回归模型：regpoly0/regpolyl/regpoly2。

23、s32、选择dace库中相关模型：guass/exp/expg/lin/spline/spherical；

24、s33、对于加工参数格点(ssi，dcj)，使用训练集训练，得到kriging代理模型krigij；遍历所有加工参数格点，得到全体kriging代理模型用于后续稳定性预测与分析。

25、优选的，所述步骤s4中在动态模态参数上利用kriging代理模型预测加工稳定性的方法为：

26、s41、根据旋转主轴上的模态参数测量结果，利用最小二乘法将模态参数w拟合成随着主轴转速变化的二次函数w＝f(ss)；

27、s42、对于加工参数格点(ssi，dcj)，利用1)中拟合函数计算此时的模态参数wi＝f(ssi)，利用对应模型krigij预测对应此时模态参数wi的系统转移矩阵谱半径与预测均方误差mseij：

28、

29、s43、遍历所有加工参数格点，全体预测结果构成谱半径矩阵和均方误差矩阵m，其中：

30、

31、m＝{mseij|i＝0，...，m；j＝0，...，n}#(7)

32、类似全离散法，通过对求1-等高线可以得到此方法预测出的稳定性叶瓣图；

33、s44、计算稳定性叶瓣图鲁棒下界：

34、选择合适的正整数t，通过给谱半径矩阵加t倍的均方误差矩阵，并求解1-等高线，可以得到更为鲁棒的稳定性叶瓣图的下界，其中：

35、

36、本发明的有益效果在于：

37、1.基于概率框架和模态参数动态建模的不确定性度量：在现有的基于概率框架的加工颤振稳定性预测方法中，往往只考虑了由模型简化和测量误差造成的系统不确定性，无法对模态参数随加工策略、加工状态的时变性质进行精确度量。本发明在使用概率框架度量模型不确定性的同时，研究了旋转主轴上的动模态分析结果，并通过引入模态参数域上的kriging代理模型实现不确定性的传导。最终得到了鲁棒性更好，精确度更高的稳定性叶瓣图。其中，在使用概率框架度量模态参数不确定性时，选择建立系统模态参数(切削力系数与刀尖动力学参数)的独立联合正态分布，利用平均切削力模型拟合的切削力系数与多次冲击实验测量出的动力学参数平均值作为联合分布的均值，根据动模态分析结果适当选择联合分布的方差。之后从联合分布中采样若干组带有不确定性的模态参数，并利用传统离散稳定性分析方法计算得到这组采样结果下kriging代理模型的训练集。最终，通过利用训练后的kriging代理模型预测出动模态参数上鲁棒性更好，精确度更高的稳定性叶瓣图。

38、2.基于动模态分析结果的参数分布方差选择：本发明在构建模态参数联合分布时，选择合适的参数分布方差可以提高预测结果的准确度，降低样本数量与模型计算成本。在传统的不确定度量方法中，一般统一选择参数均值的10％-20％作为分布方差。但这样的过于宽泛的方差选择会导致在采样时产生许多与真实切削系统不匹配的模态参数值，从而导致采样质量的下降。

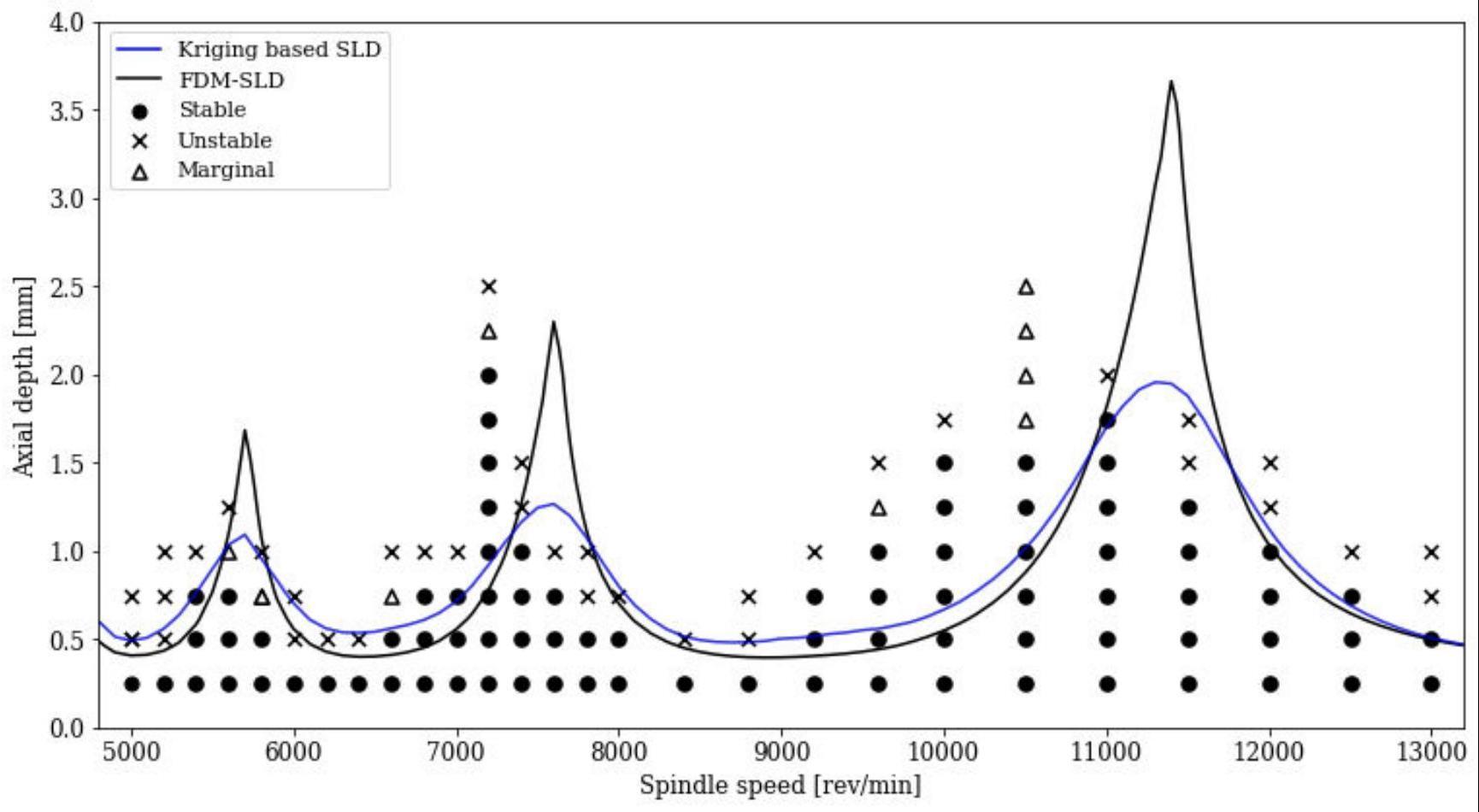
39、本发明通过研究待预测加工参数域上的动模态分析结果，计算出模态参数在不同主轴转速下的拟合值。最终针对分布均值[0.7827,0.7528,0.0184,0.0186,6.56,4.88,10.95,1.76]，选择方差对角阵为0.0001*np.diag([7,7,0.10,0.15,10,15,10,5])，使得采样结果上界落在第二个波峰(rpm＝7500)所对应的模态参数拟合值附近，这保证了训练集中模态参数主要分布在低转速区域，在高转速区域(rpm>7500)中，预测稳定性边界与切削实验结果有着更好的匹配度。

40、3.基于模态参数重要性的kriging相关模型系数选择：在铣削动力学模型中，不同的模态参数对模型的不确定性有着不同程度的影响。本发明通过参考对模态参数的灵敏度分析(sensitivity analysis，sa)结果，在选择kriging相关模型系数上下界时，通过对不同重要程度的参数设置不同的相关模型系数变化范围，实现了对模型不确定性的更准确度量。其中，根据灵敏度分析结果，由于模态参数中刀尖动力学参数对不确定性的影响要显著大于切削力系数的影响。因此，在选择kriging代理模型的相关系数上下界时，针对径向/轴向切削力系数选择参数变化区间[1e-2,5]，针对动力学参数中的系统固有频率、阻尼比，选择参数变化区间[1e-1,10]。通过对动力学参数对应的相关系数选择更大的上界以及更宽的变化区间，可以提高kriging代理模型预测结果中重要程度更高的系统参数的影响比重，最终得到更为精确的稳定性边界。