一种基于碰撞原理分选退役光伏电池颗粒数值模拟方法

本发明涉及固体废品回收，尤其是涉及一种基于碰撞原理分选退役光伏电池颗粒数值模拟方法。

背景技术：

1、在全球范围内，光伏的装机总量都在逐年增加，预计今年达到1tw。然而，光伏组件的平均寿命预估在25到30年。随着时间的推移，报废光伏组件的数量也在逐年增涨，预计到2030年达到百万吨级，到2050年达到惊人的960万吨，这必然会面临退役光伏组件的处理问题。如果直接将退役光伏组件做填埋处理，其中的有毒物质会对环境造成污染并且有价值的成分因得不到合理回收而白白浪费。因此无论从经济角度还是环保角度对废弃光伏组件进行回收都是有必要的。

2、对于退役光伏组件的回收大都采用化学方法、热解法和机械破碎法，前两种方法难免会对环境造成污染，后种方法相较于前种方法，环境问题有所改善，但是分选效率不高。为提高机械破碎法的分选效率，在破碎过程中加入分选流程，从环保角度出发先对破碎之后的产物进行逐级筛分，之后进行逐级分离。在分离金属破碎物的过程中可以采用静电分选的方法。

3、在工业领域中，电晕辊式静电分选器被广泛使用。电晕辊式静电分选器由振动给料机、接地辊、电晕电极、静态电极(截面形状为圆形)、收集槽以及毛刷组成。在其工作过程中，需要调节的装置参数众多，这也就为得到理想的分离效率带来难题，而数值模拟不仅可以将静电分选过程中各参数对颗粒轨迹的影响以直观的形式表现出来还能够为后续装置参数的调节提供参考，这将大大减少因参数调整而造成的资源浪费以及提高分选效率，因此数值模拟成为静电分选器调整相关参数过程中必不可少的环节。本发明针对采用静电分选法对退役光伏电池颗粒进行回收的过程中，因需要调整的参数过多不能有效调节导致分选效率低下这一问题，提出一种基于碰撞原理分选退役光伏电池颗粒的数值模拟方法。

技术实现思路

1、本发明要解决的技术问题是：为了解决采用静电分选法对光伏电池颗粒进行回收的过程中，需要调整的参数过多，分选效率低下的问题，现提供了一种基于碰撞原理分选退役光伏电池颗粒数值模拟方法。

2、本发明解决其技术问题所采用的技术方案是：一种基于碰撞原理分选退役光伏电池颗粒数值模拟方法，包括步骤如下：

3、s1、建立电晕辊式静电分选器内腔简化物理模型，所述简化模型为平面模型；

4、s2、选取物理场模块；

5、s3、设置平面区域内介质材料属性参数；

6、s4、设置边界条件以及各类电极的初始条件；

7、s5、划分网格；

8、s6、提交作业及后处理；

9、s7、建立颗粒理论轨迹模型；

10、s8、选取数值求解方法进行求解。

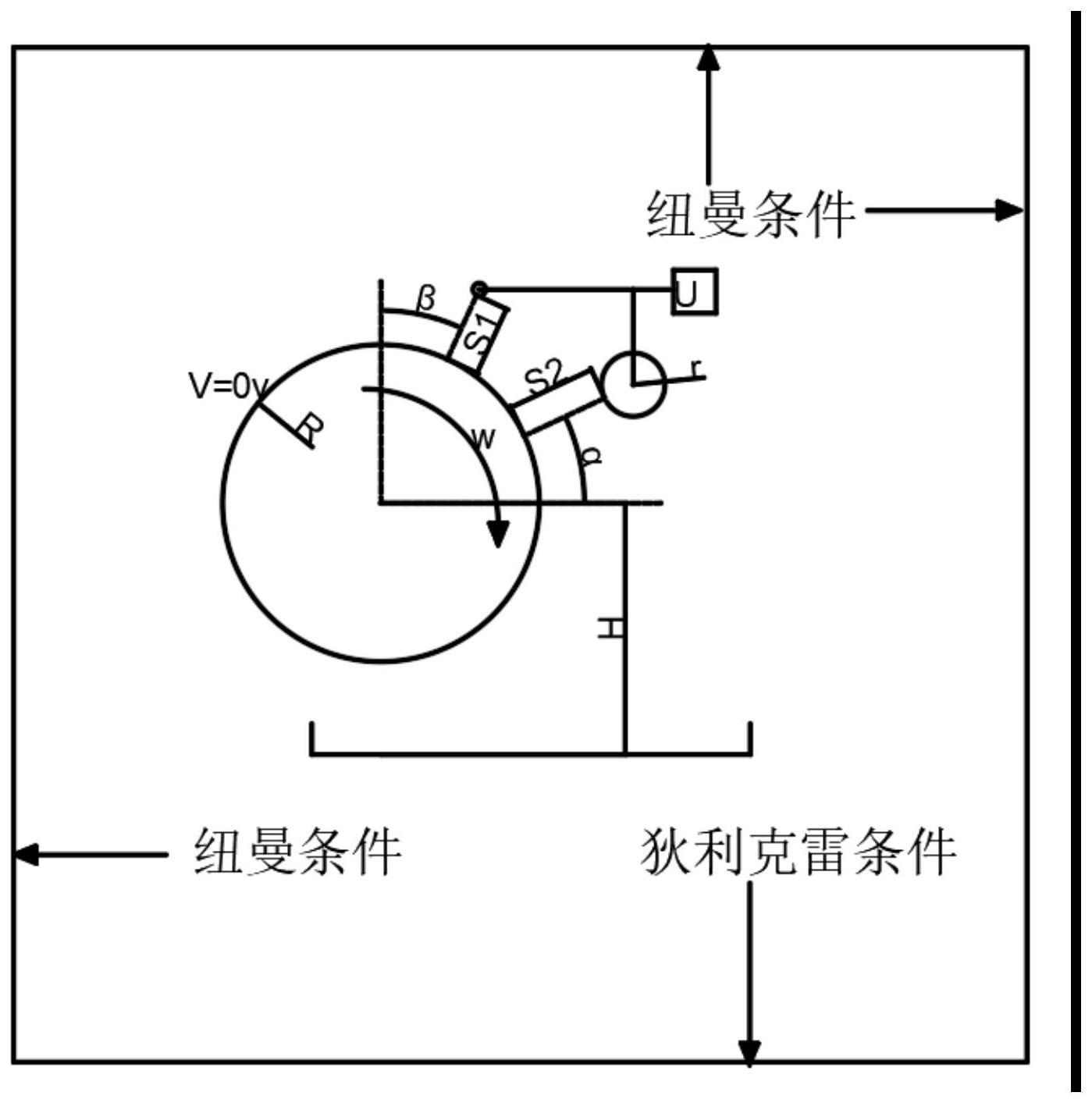
11、优选地一些实施方式，步骤s1中建立电晕辊式静电分选器内腔简化物理平面模型，该模型处于正方形区域中，最大的圆形为接地辊电极，最小的圆形为电晕电极，处于中间大小的圆形为静态电极，所述静态电极圆形区域内部是空心。

12、优选地一些实施方式，步骤s2中所选用的物理场模块为等离子体模块下的电晕放电模块，该模块的控制方程式如下：

13、

14、其中方程式(1)为电荷守恒方程，e是空间电场强度(v/m)，ρ是空间电荷密度(c/m3)，ε0空间介电常数；

15、

16、其中方程式(2)为连续性方程，j是电流密度(a/m2)；

17、

18、其中方程式(3)为电流密度方程，j是电流密度(a/m2)，μ是离子迁移率，e是空间电场强度(v/m)；

19、

20、其中方程式(4)为电荷守恒方程，φ是电势，e是空间电场强度(v/m)；

21、

22、其中方程式(5)为泊松方程，ρ是空间电荷密度(c/m3)，ε0空间介电常数，φ是电势。

23、优选地一些实施方式，步骤s4中区域上边界，左边界以及右边界采用纽曼条件，区域的下边界采用狄利克雷边界条件，其中设置接地辊设置初始电压为0伏特，静态电极以及电晕电极设置的初始电压为u千伏并接入电源正极，电极内部不导电，平面区域内部初始电压为0伏特。

24、优选地一些实施方式，所述电极条件产生的电场遵循peek准则：

25、

26、方程式(6)中，e0是击穿电场(v/m)，δ是在760torr，293.15k条件下归一化到气体密度的气体数密度，ri为电晕电极半径(mm)。

27、优选地一些实施方式，步骤s5在模拟软件中设置网格大小以及网格形状。

28、优选地一些实施方式，步骤s6在模拟软件中提交作业并进行分析，得到平面区域内电场强度的分布数值，并对数据进行处理。

29、优选地一些实施方式，步骤s1-步骤s6在comsol multiphysics 6.0中进行。

30、优选地一些实施方式，步骤s7中的理论轨迹方程基于以下四个假设：第一个假设为颗粒形状为球形，第二个假设为材料是单层分布在接地辊表面并且随其一起运动，第三个假设为两个相邻颗粒之间的距离非常大，并且每个粒子都可以由一个带有材料属性的点近似，第四个假设为忽略颗粒之间的相互作用；

31、其中步骤s7中颗粒在离开接地辊表面进入空间电场之前，颗粒受库仑力fe，离心力fc，重力fg的作用；

32、上述颗粒在离开接地辊电极之前受到的电场力为fe＝0.832qde   (7)；

33、上述颗粒在离开接地辊电极之后受到的电场力为fe＝qde       (8)；

34、上述方程式(7)以及方程式(8)中

35、

36、其中方程式(7)、方程式(8)和方程式(9)中qd为颗粒电荷(c)，rp为颗粒粒径(mm)，ε为介电常数，e(x0,y0)为分离点处的电场数值(v/m)；

37、上述离心力

38、其中方程式(10)中rp为颗粒粒径(mm)，ρmaterial为颗粒的密度(kg/m3)，ω为接地辊的转动速度(rad/s)，r为接地辊半径(m)，g为重力加速度，其值为9.8m/s2；

39、上述颗粒重力

40、其中方程式(11)中rp为颗粒粒径(mm)，ρmaterial为颗粒的密度(kg/m3)，g为重力加速度，其值为9.8m/s2；

41、其中步骤s7中的理论轨迹方程根据上述力学公式求解颗粒离开接地辊时的分离角

42、θd：fg×cos(θd)-fe-fc＝0                                    (12)；

43、其中步骤s7中的颗粒在下落阶段主要受库仑力fe，重力fg，以及空气阻力fd；

44、上述空气阻力fd＝6πrpηv                                     (13)；

45、其中方程式(13)中η为空气动态黏度，其值为1.81×10-5kg/ms，v为颗粒速度(m/s)；

46、在步骤s7中的理论轨迹方程如下：

47、分离时刻线速度在x方向的分量：

48、vx(x0,y0)＝ωrcos(θd)                                          (14)；

49、其中方程式(14)中，vx(x0,y0)为进颗粒进入电场初始时刻的水平方向的速度(m/s)，ω为接地辊电极的角速度(rad/s)，r为接地辊电极半径(mm)，θd为分离角(rad)；

50、分离时刻线速度在y方向的分量：

51、vy(x0,y0)＝-ωrsin(θd)                                           (15)；

52、其中方程式(15)中，vy(x0,y0)为进颗粒进入电场初始时刻的竖直方向的速度(m/s)，ω为接地辊电极的角速度(rad/s)，r为接地辊电极半径(mm)，θd为分离角(rad)；

53、加速度在x方向的分量：

54、其中方程式(16)中ax(xi,yi)为颗粒在第i迭代步时水平方向的加速度(m/s2)，η为空气动态黏度，其值为1.81×10-5kg/ms，rp为颗粒粒径(mm)，vx(xi,yi)为颗粒在第i迭代步时水平方向的速度(m/s)，qd为颗粒电荷(c)，ex(xi,yi)为在第i迭代步时电场强度在水平方向的分量(v/m)，m为颗粒的质量(kg)；

55、加速度在y方向的分量：

56、其中方程式(17)中ay(xi,yi)为颗粒在第i迭代步时竖直方向的加速度(m/s2)，η为空气动态黏度，其值为1.81×10-5kg/ms，rp为颗粒粒径(mm)，vy(xi,yi)为颗粒在第i迭代步时竖直方向的速度(m/s)，qd为颗粒电荷(c)，ey(xi,yi)为在第i迭代步时电场强度在竖直方向的分量(v/m)，m为颗粒的质量(kg)；

57、速度在x方向的分量：vx(xi,yi)＝vx(xi-1,yi-1)+ax(xi-1,yi-1)dt            (18)；

58、其中方程式(18)中，vx(xi,yi)为颗粒在第i迭代步时水平方向的速度(m/s)，vx(xi-1,yi-1)为颗粒在第i-1迭代步时水平方向的速度(m/s)，ax(xi-1,yi-1)为颗粒在第i-1迭代步时水平方向的加速度(m/s2)，dt为时间变化量；

59、速度在y方向的分量：vy(xi,yi)＝vy(xi-1,yi-1)+ay(xi-1,yi-1)dt           (19)；

60、其中方程式(19)中，vy(xi,yi)为颗粒在第i迭代步时竖直方向的速度(m/s)，vy(xi-1,yi-1)为颗粒在第i-1迭代步时竖直方向的速度(m/s)，ay(xi-1,yi-1)为颗粒在第i-1迭代步时竖直方向的加速度(m/s2)，dt为时间变化量；

61、x方向的位移方程：xi＝xi-1+vx(xi-1,yi-1)dt+0.5ax(xi-1,yi-1)dt2        (20)；

62、其中方程式(20)中，xi为颗粒在第i迭代步时的横坐标，xi-1为颗粒在第i-1迭代步时的横坐标，vx(xi-1,yi-1)为颗粒在第i-1迭代步时水平方向的速度(m/s)，ax(xi-1,yi-1)为颗粒在第i-1迭代步时水平方向的加速度(m/s2)，dt为时间变化量；

63、y方向的位移方程：yi＝yi-1+vy(xi-1,yi-1)dt+0.5ay(xi-1,yi-1)dt2          (21)；

64、其中方程式(21)中，yi为颗粒在第i迭代步时的纵坐标，yi-1为颗粒在第i-1迭代步时的纵坐标，vy(xi-1,yi-1)为颗粒在第i-1迭代步时竖直方向的速度(m/s)，ay(xi-1,yi-1)为颗粒在第i-1迭代步时竖直方向的加速度(m/s2)，dt为时间变化量；

65、其中的理论轨迹方程还包括碰撞方程，并从理论角度出发因此选用弹性碰撞方程来描述这一过程；

66、当颗粒与静态电极发生碰撞的那一瞬间，颗粒所受电场力的方向就会发生变化(与原来方向相反)，大小相等，即：

67、

68、其中方程式(22)中，为颗粒在第i迭代步发生碰撞之后的电场力(n)，为颗粒在第i迭代步发生碰撞之前的电场力(n)；

69、其中颗粒与静态电极发生的碰撞为弹性碰撞，该过程满足动量守恒定律，速度变化如下：

70、碰撞后颗粒的切向速度为：

71、其中方程式(23)中，为颗粒发生碰撞之后的切向速度(m/s)，为颗粒发生碰撞之前的切向速度(m/s)；

72、碰撞后颗粒的法向速度为：

73、其中方程式(24)中，为颗粒发生碰撞之后的法向速度(m/s)，为颗粒发生碰撞之前的法向速度(m/s)；

74、其中颗粒与静态电极发生的碰撞为弹性碰撞，该过程中颗粒的入射角应当等于反射。

75、优选地一些实施方式，步骤s8中选用数值迭代的求解方法，计算出颗粒的运动轨迹。

76、本发明的有益效果是：本发明一种基于碰撞原理分选退役光伏电池颗粒数值模拟方法在使用时，采用基于碰撞原理分选退役光伏电池颗粒的数值模拟方法，可以为工程应用过程中静电分选装置参数的调节提供参考，这将大大减少因参数的调整而导致的严重资源浪费以及提高分选效率，因此，该方法的合理利用，节约了固废回收企业的投入成本，还在提高回收效率的同时起到了保护环境的作用，避免了现有采用静电分选法对光伏电池颗粒进行回收的过程中，需要调整的参数过多，分选效率低下的问题。