一种快速控制井筒温度的计算方法

本发明涉及石油开采钻井领域，具体涉及一种快速控制井筒温度的计算方法。

背景技术：

1、在钻井过程中，钻井液从地面钻井泵注入钻柱内，再经过钻头喷嘴经钻柱与套管形成的环形空间流出井筒。在流动的同时会与地层发生热交换，使得钻井液温度上升，特别是在深井与超深井的钻进过程中，这会导致钻井液的塑性粘度下降，密度减小，其携岩性能也会随之下降。高温不仅仅影响钻井液的性能，也对井下作业工具的寿命、机械转速、井壁稳定性等产生影响。因此有必要将井筒-地层的温度控制到合理的范围以满足生产所需。

技术实现思路

1、针对现有技术中的上述不足，本发明提供的一种快速控制井筒温度的计算方法可以实现快速控制井筒温度。

2、为了达到上述发明目的，本发明采用的技术方案为：

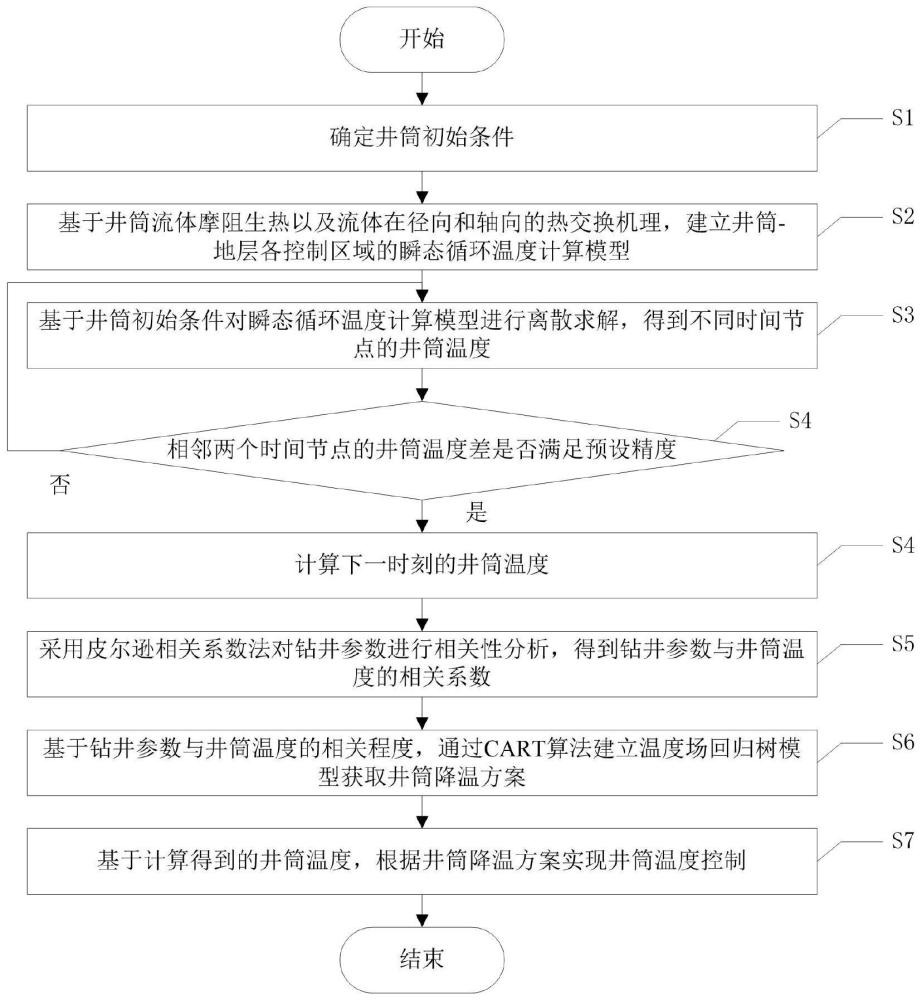
3、提供一种快速控制井筒温度的计算方法，其包括以下步骤：

4、s1、确定井筒初始条件；

5、s2、基于井筒流体摩阻生热以及流体在径向和轴向的热交换机理，建立井筒-地层各控制区域的瞬态循环温度计算模型；

6、s3、基于井筒初始条件对瞬态循环温度计算模型进行离散求解，得到不同时间节点的井筒温度；

7、s4、判断相邻两个时间节点的井筒温度差是否满足预设精度，若是则计算下一时刻的井筒温度并进入步骤s5；否则返回步骤s3；

8、s5、采用皮尔逊相关系数法对钻井参数进行相关性分析，得到钻井参数与井筒温度的相关系数；

9、s6、基于钻井参数与井筒温度相关程度，通过cart算法建立温度场回归树模型获取井筒降温方案；

10、s7、基于计算得到的井筒温度，根据井筒降温方案实现井筒温度控制。

11、进一步地，步骤s1中井筒初始条件包括钻杆、套管层次、水泥环的尺寸、热物理参数、钻井液的流变性、钻井液的密度、钻井液的比热容，以及泵入的排量。

12、进一步地，步骤s2中瞬态循环温度计算模型包括钻柱内钻井液温度子模型、钻柱壁温度子模型、环空钻井液温度子模型和近井壁传热子模型；其中，钻柱内钻井液温度子模型的表达式为：

13、

14、在钻柱内钻井液温度子模型中，钻井液与钻杆内壁之间的边界条件表达式为：

15、

16、其中ρ1为钻井液的密度；cp1为钻井液的比热容；t1为钻杆内流体的温度；t表示时间；z表示轴向方向；vz1为钻井液在钻杆内部的轴向流速度；λ1为钻井液的热导率；r表示离钻柱轴芯的距离；r1为钻柱半径；h1为钻杆内壁的对流换热系数；t2为钻柱壁温度；

17、钻柱壁温度子模型的表达式为：

18、

19、在钻柱壁温度子模型中，钻杆内部流体与钻杆壁之间的边界条件表达式为：

20、

21、在钻柱壁温度子模型中，环空流体与钻杆壁之间的边界条件表达式为：

22、

23、其中ρ2为钻柱的密度；cp2为钻柱的比热容；λ2为钻柱的热导率；r2为钻柱的外半径；h3为钻杆外壁的对流换热系数；t3为环空流体的温度；

24、环空钻井液温度子模型的表达式为：

25、

26、

27、在环空钻井液温度子模型中，从地层由热传导方式传到井壁热量与井壁流体经热对流和热传导方式流入环空的热量相等，其表达式为：

28、

29、其中ρ3为环空流体密度；cp3为环空流体比热容；t3为环空流体温度；vz3为环空钻井液轴向速度；λ3为环空流体热导率；vr为地层中流体的速度；hef为考虑地层多孔性影响的井壁面对流换热系数；t4为井壁温度；λef为考虑了多孔性流体影响的地层有效热导率；tf为地层温度；r3为井眼半径；

30、近井壁传热子模型的表达式为：

31、

32、(ρcp)ef＝φ(ρcp)s+(1-φ)(ρcp)l

33、vr＝f(φ,m,mfu,ρin,al)

34、

35、在近井壁传热子模型中，钻井液入口和井筒温度的初始条件为：

36、t1(r,0,t)＝tin

37、tk(r,z,t)＝ts+gd

38、其中(ρcp)ef为环绕井筒区域的热容量；ti为地层多孔介质中不同单位的温度；ri为地层多孔介质的半径；φ为地层孔隙度；(ρcp)s为岩石的热容量；(ρcp)l为孔隙流体的热容量；k为各向同性多孔介质的绝对渗透率；μ为地层中流体的动态粘度；p为地层中流体的内在平均压力；m为钻井液的质量流量；mfu为地层中流体的质量流量；ρin为地层中流体的密度；al为横向流动面积；tin为钻井液入口温度；t1(r,0,t)表示钻杆中与轴芯距离为r、与杆口距离为0、时间为t时的流体温度；tk(r,z,t)为井筒和地层在与轴芯距离为r、与井口轴向距离为z、时间为t时的温度；ts为地表温度；g为地温梯度；d为井深。

39、进一步地，步骤s3中离散求解的表达式为：

40、

41、其中为第v+1次迭代时在径向第i个空间网格节点、轴向第j个空间网格节点处时间节点为n+1的井筒温度；ω为松弛参数；bi,j、fi,j、ai,j、ci,j、di,j、ei,j分别为对应温度节点系数；为第v次迭代时在径向第i个空间网格节点、轴向第j个空间网格节点处时间节点为n的井筒温度；为第v+1次迭代时在径向第i-1个空间网格节点、轴向第j个空间网格节点处时间节点为n+1的井筒温度；为第v次迭代时在径向第i+1个空间网格节点、轴向第j个空间网格节点处时间节点为n+1的井筒温度；为第v+1次迭代时在径向第i个空间网格节点、轴向第j-1个空间网格节点处时间节点为n+1的井筒温度；为第v次迭代时在径向第i个空间网格节点、轴向第j+1个空间网格节点处时间节点为n+1的井筒温度；为第v次迭代时在径向第i个空间网格节点、轴向第j个空间网格节点处时间节点为n+1的井筒温度。

42、进一步地，步骤s5中进行相关性分析的具体方法为：

43、根据公式：

44、

45、获取钻井参数x和井筒温度y的相关系数rx,y；其中xi和yi分别为钻井参数x和井筒温度y的观测值；和分别表示钻井参数x和井筒温度y的平均值；n表示样本数量。

46、本发明的有益效果为：

47、1、本发明考虑了每个控制区域在径向和轴向上的传热机理，建立了井筒-地层各控制区域二维瞬态循环温度计算模型，使得该模型更能全面的表征井筒-地层各控制区域的热交换效率；

48、2、本发明在数学模型离散化处理后，求解采用径向和轴向上的隐式和显示组合的半时间步长下的有限差分计算方法。比常规的显示差分算法更加的快速收敛效果也更好，能够更加快速的应用于现场实践。

49、3、本发明采用皮尔逊相关系数法分析各单因素对井筒温度的影响程度；在此基础上采用cart算法方法对多参数进行优化，将机器学习的方法同传统理论研究相结合，综合考虑多钻井参数之间的相互影响，确定影响井筒温度的关键参数，进而最大程度降低井筒温度，形成了一种快速控制井筒温度的计算方法。