一种复杂几何体无网格自适应离散方法和系统

本方案属于科学计算、计算物理、人工智能、工业数字孪生领域，涉及复杂构型、任意运动/静止边界下几何体的离散方法，提出了一种复杂几何体无网格自适应离散方法和系统，基于图神经网络深度强化学习方法实现。

背景技术：

1、网格离散方法已经广泛应用于工程、物理、生物等领域的模拟和计算中，而且是现在进行区域离散化和数值离散化的主要方法，工程应用和数值理论上的研究相当成熟。然而，基于网格的数值模拟前提条件是在问题域生成网格，这就使得它天然地具有一定的局限性。在不规则或者很复杂的几何形状上构造出高质量的网格是一件很困难的事情，并且通常需要进行复杂的数学转换，这些数学转换甚至比求解问题的本身还要麻烦和繁琐；同时，在固定的欧拉网格上精确确定自由表面、变形边界、运动交界面和不均匀介质之间的位置也是一项很困难的工作。对于运动边界问题有时生成动网格是必要的，大变形问题中还需要网格重分重映，这些工作非常繁琐而且耗时，有时还会造成错误。事实上，传统的数值模拟方法开展数值计算时，很大一部分时间开销在于生成高质量的网格，对于以上复杂问题基于网格的数值方法往往难以有效解决。

2、随着计算技术的不断发展，基于物质点方法的计算物理学不断得到发展。考虑到各种典型工程问题的类型特征以及网格方法的局限性，无网格物质点方法(meshlessmethods)应运而生，最有可能为这些复杂问题提供容易实现的解决方案。它完全抛弃了网格这个工具进行计算，通过使用一系列任意分布的节点来求解具有各种各样初边值条件的偏微分方程组(pde)从而完成数值计算，例如中国专利公开的基于无网格法的高精度几何模型粒子离散方法、装置及系统(公开号cn113761778b)。这些节点之间不需要网格进行衔接，无固定的拓扑关系，通过追踪物质点的运动就可以很容易地得到整个物理系统的特性。按计算的物质尺度，无网格物质点模拟方法可从最小的第一性原理模拟尺度到分子或分子团尺度进而延伸到宏观尺度，提供了从微观、介观到宏观不同尺度的统一形式的描述手段。在科学与工程领域存在众多应用，包括微流动和生物流动(微液滴动力行为、高分子悬浮与输运、细胞变形、粘附与运移等)，环境与地质流动(多孔介质与裂隙网络中多相流动、溃坝、泥石流等)，自由液面流动(波浪砰击、液体晃荡、结构出入水、溢油拦截等)。

3、类似于网格方法，在无网格方法体系下基于节点描述对复杂几何体进行高效离散和自适应分割是数值计算工作流程中一个重要瓶颈。自适应节点划分技术允许节点自动更新，为当前问题提供准确的解决方案。然而既有的经典自适应节点划分技术在处理复杂几何体时依然相当繁琐，要么需要求解器之外的附加计算，要么需要许多次模拟。以gpt技术为代表的生成式人工智能方法飞速发展，使得机器学习在处理这类繁琐复杂的问题上表现出诱人的发展潜力。但是，当前机器学习方法存在三个显著的不足：(1).主要面向传统的网格划分问题，对于无网格节点或粒子的生成和优化研究相对缺乏；(2).通常需要大量的计算成本来生成训练数据，不利于工程应用；(3).在应用范围上受限于训练数据流机制，可迁移性和扩展性较差。

4、为了解决上述问题，本发明开发了一个基于图神经网络的通用深度强化学习(deep reinforcement learning，drl)无网格自适应离散框架，以不断迭代的方式来优化数值计算的节点拓扑。该技术框架以图的观点描述离散节点分布，通过融合图节点拓扑与数值计算精度和效率指标进行强化学习。同时，该方法面向任意复杂物理场的模拟场景，将传统的严重依赖人工的繁琐工作降低到最小化程度，能够满足大规模科学计算的需求，在工业数字孪生领域具有很强的应用前景。

技术实现思路

1、本方案的目的是针对上述问题，为工业领域大规模、高性能科学计算提供一种全流程智能化的复杂几何体离散前处理流程。该方法基于无网格思想和图神经网络深度强化学习方法，旨在克服基于无网格方法对复杂几何体进行自适应前处理的困难，实现对任意复杂几何体自动化和智能化地离散。

2、鉴于此，本方案提供一种基于图神经网络深度强化学习方法的复杂几何体无网格自适应离散方法，同时，方法所提出的图神经网络深度强化学习离散框架在工业数字孪生领域具有很强的应用前景，本方案对此提出一种工业数字孪生系统，该数字孪生系统应用该离散方法对所涉及到的复杂几何体进行离散处理，以提高孪生系统的建模精度以及数据处理和分析能力。

3、一种复杂几何体无网格自适应离散方法，该方法基于图神经网络深度强化学习方法实现，该方法包括：

4、s1.针对任意复杂几何体，在不考虑边界特征的情况下，采用正交离散将其剖分为一系列规则的微元面/体，辅助背景网格从最近邻边界单元的微元面/体开始在给定的支撑域内进行邻居点搜索，即设置支撑域大小，根据是否位于支撑域内部确定是否邻近，根据邻近边界单元判据构建几何体内点集合，进而生成一张由节点和边组成的图网络结构，实现对其初始化离散；

5、s2.采用深度强化学习方法逐一对每个中心节点的局部子图结构进行自适应地迭代和调整；

6、s3.基于更新的离散图节点状态所携带的拓扑结构和物理信息，采用多尺度残差卷积神经网络提取物理场非线性模式特征，进而耦合跨尺度图卷积算子经由层级时空神经网络层对物理场进行时空演化；

7、s4.以数值计算的精度和效率为优化目标，通过智能体的动作和环境之间的信息交互找到一个最优的行动选择策略使奖励最大化，最终自动实现对复杂几何体最优化的离散和剖分。

8、在上述的复杂几何体无网格自适应离散方法中，步骤s1中，针对任意复杂几何体，在不考虑边界特征的情况下，采用正交离散将其剖分为一系列规则的微元面/体具体包括：

9、s1-1.针对任意复杂几何体，按照二维或三维构型进行分类，根据其包络边界的不同，依次分解为边界线(直线或曲线)或边界面(平面或曲面)；

10、s1-2.构建几何边界类：点、线和面；

11、s1-3.确定整个几何实体的远端边界位置坐标：[xmin,xmax]、[ymin,ymax]、[zmin,zmax]，并根据背景网格各个方向离散尺度dx_grid,dy_grid和dz_grid划分背景网格；

12、其中，xmin和xmax分别为几何体的x轴最左端和最右端坐标；ymin和ymax分别为几何体的y轴最左端和最右端坐标；zmin和zmax分别为几何体的z轴最左端和最右端坐标；

13、s1-4.确定几何体各个方向离散尺度dx,dy和dz，根据远端边界位置坐标：[xmin,xmax]、[ymin,ymax]、[zmin,zmax]，在不考率边界特征的情况下，将其剖分为规则的微元面(二维，其面积大小为：dx×dy)或微元体(三维，其体积大小为：dx×dy×dz)；

14、在上述的复杂几何体无网格自适应离散方法中，步骤s1-2中，对于任意边界线/直线/曲线统一离散为多个微元线，每个微元基于位置坐标、线段长度和法向量进行描述；对于任意边界面/平面/曲面统一离散为多个微元面，每个微元基于位置坐标、微元面积和法向量进行描述。

15、在上述的复杂几何体无网格自适应离散方法中，步骤s1中，辅助背景网格从最近邻边界单元的微元面/体开始在给定的支撑域内进行邻居点搜索具体包括：

16、s1-5.根据背景网格各个方向的离散尺度，依次将上述几何体边界微元线段或边界微元面以及每一个离散的微元面或微元体嵌入对应的背景网格；

17、s1-6.统计嵌入边界单元的背景网格，对于其内部嵌入的离散微元体(面)逐一搜索最邻近的边界单元，计算相对边界单元的距离矢量dr＝rnode-rboundary，判断边界元法向量与相对距离矢量的内积flag＝dr·n，进而确定离散微元体(面)是否为几何体的内点，并将几何体的内点形成一个集合；

18、其中，rnode和rboundary分别为离散微元体(面)和边界单元的坐标位置；n为边界微元法向量；

19、在上述的复杂几何体无网格自适应离散方法中，步骤s1-2中，根据邻近边界单元判据构建几何体内点集合，进而生成一张由节点和边组成的图网络结构具体包括：

20、s1-7.对于上述s1-6步骤中几何体内点集合，按照给定的支撑域大小继续搜索，对于搜索到的邻居离散微元体，判断其是否处于边界单元附近，对于边界单元附近的离散微元体，按照第s1-6步骤判断是否将其加入几何体内点的集合；对于远离边界元的离散微元体，直接加入几何体内点的集合；

21、s1-8.循环重复s1-7，不断更新每一个背景网格中嵌入的离散微元体状态，直至每一个离散微元体均被搜索完毕，至此几何体内点集合便形成了初步离散结果。

22、在上述的复杂几何体无网格自适应离散方法中，步骤s2具体包括：

23、s2-1.基于初始化离散图节点确定潜在的动作at集合，其中动作at类型包括离散图节点的位置调整、删减和分裂；位置调整动作适用于所有的离散图节点，而删减和分裂适用于临近边界以及需要特殊加密处理的区域；

24、s2-2.对于s2-1中远离边界以及需要特殊加密处理区域的离散图节点，基于其位置坐标以及离散尺度正相关的支撑域大小δ，确定其位置调整的区域：[xnode-δ,xnode+δ]、[ynode-δ,ynode+δ]、[znode-δ,znode+δ]；

25、其中，xnode，ynode和znode分别为远离边界以及需要特殊加密处理区域的离散图节点坐标；

26、s2-3.对于s2-2中位于临近边界以及需要特殊加密处理区域的离散图节点，确定与边界元距离相关的自适应缩尺因子将一个父节点分裂为多个子节点(num＝[ratio])，其中每个子节点分布在与父节点离散尺度正相关的支撑域δf内：[xfather_node-δf,xfather_node+δf]、[yfather_node-δf,yfather_node+δf]、[zfather_node-δf,zfather_node+δf]；

27、其中，ratio为父节点分裂为子节点的体积缩尺因子，vnode为子节点体积，vfather_node为父节点体积；num为父节点分裂为子节点的个数，[]代表取整运算；δf为父节点支撑域大小；xfather_node，yfather_node和zfather_node分别为远离边界以及需要特殊加密处理区域的离散图节点坐标；

28、s2-4.对当前的离散图节点选择动作at编码构造新的子图结构。

29、在上述的复杂几何体无网格自适应离散方法中，步骤s3具体包括：

30、s3-1.确定模拟场景的特征，归纳出典型案例的特征数据，并总结几类初边值条件类型以及可能的内外扰动形式，形成完备的模拟案例集合；

31、s3-2.对于每一个典型的模拟案例基于步骤s1和s2进行几何离散化表征；

32、s3-3.在离散的节点上施加模拟需要的初边值条件，根据计算域离散化的图节点空间分布进行结构关联，预估物理场中任一图节点的影响域和依赖域大小，并初始化其邻居点链表；

33、s3-4.在模拟区域边界基于不同的边界条件类型构造虚拟节点，根据不同的图节点位置相应的初边值条件通过消息传递的方式施加“硬约束”，从而保证在物理场模拟过程中这些约束被严格施加给模拟区域；

34、s3-5.构建多尺度残差卷积神经网络，逐一在计算域离散图节点上提取物理场非线性模式特征；

35、s3-6.将s3-5提取的物理场非线性模式特征传递至层级时空神经网络层，基于跨尺度图卷积算子通过消息传递的方式在计算域离散图节点(包括虚拟节点)之间进行动态交互，进而实现物理场的时空演化。

36、在上述的复杂几何体无网格自适应离散方法中，步骤s4中，融合图节点拓扑与数值计算精度和效率指标进行强化学习。

37、在上述的复杂几何体无网格自适应离散方法中，步骤s4具体包括：

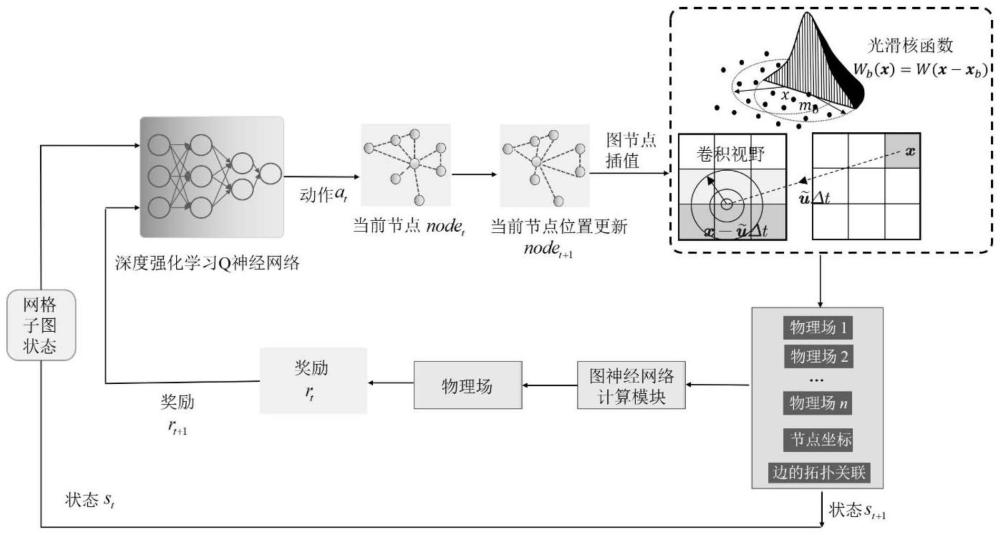
38、s4-1.将当前中心节点的子图结构输入到图神经网络计算模块进行一次数值模拟，从模拟的结果数据中提取物理场、节点的坐标和边的拓扑关联等数据并将其作为智能体当前的状态；

39、s4-2.图神经网络对当前中心节点的子图结构做出判断并确定其潜在的动作at集合，根据s2-2和s2-3选择动作at进而编码构造新的子图结构；

40、s4-3.对更新后的节点分布进行局部平滑，采用光滑核函数将原来的物理场插值到新的子图结构得到新的状态，并根据s4-2进行迭代计算；以第t个迭代步骤为例，在这一环节基于状态变量st评估各物理场性能指标以及模拟精度和效率等属性并据此计算出奖励值rt；

41、s4-4.基于q函数构建通用深度q网络deep q network(dqn)度量智能体的状态-动作质量并进行强化学习；智能体通过动作与环境不断交互，当智能体进入状态st后选择动作at并导致新的状态st+1，每次行动后给予奖励rt，学习的目标是找到一个最优的行动选择策略at，使奖励rt最大化；

42、s4-5.经过多次计算迭代即可自动实现对复杂几何体最优化的离散和剖分。

43、一种工业数字孪生系统，该系统通过所述的方法对所涉及到的任意复杂几何体进行离散处理。

44、本方案的优点在于：

45、(1)提出了无网格离散的技术框架，利用图的观点基于节点描述任意几何体的离散单元，节点之间不需要网格进行衔接，无固定的拓扑关系，极大地提高了复杂几何体自适应离散的灵活性；

46、(2)融合图节点拓扑与数值计算的精度和效率进行强化学习，针对不同的物理场模拟场景，根据同一套初始化生成的离散图节点以不断迭代的方式来优化数值计算的节点拓扑，实现了复杂几何体无网格自适应离散框架的重用复用，同时，算法的通用性和标准性极大提高了其应用于不同案例的可迁移性和可扩展性；

47、(3)采用深度强化学习方法替代繁琐的传统人工操作对复杂几何体初始化离散节点拓扑进行优化调整，避免了传统机器学习方法所需的庞大训练样本，面向工业领域大规模科学计算和数字孪生的需要，可以高效地实现超大规模极端复杂几何构型的前处理流程。