一种基于Steiner最小树的防灾型骨干网架规划方法与流程

本发明属于电力系统，具体涉及一种基于steiner最小树的防灾型骨干网架规划方法。

背景技术：

1、目前已进入发展大电网、大机组的新阶段，这对电网规划设计提出了更高的要求，而输电网规划作为电网规划的关键组成部分，其对于电力系统的安全可靠运行具有十分重要的意义，具备较强破坏性的极端天气灾害事件对输电网等拥有较多暴露型设备的基础设施造成了较大的危害和损失，因此，在电网规划中亟需增强输电网对极端灾害的抵御能力，从而保障电力系统的安全性和可靠性；防灾型骨干网架是指提高电网中部分线路、杆塔和变电站的设计标准原则，并且使之形成满足拓扑连通性和系统安全稳定运行约束的核心主干网架，可用于确保系统重要负荷在极端灾害等事件突发时的供电，并为之后系统维修恢复供电奠定基础；目前，对防灾骨干网架的研究主要集中在对现有网络的改造上，主要应用于已经存在的配电网上，通过对配电网线路的重要程度进行评估确定骨干网架，但无法求解新建配电网的骨干网架；因此，提供一种综合考虑建设成本和受灾风险、增强容灾和抗灾能力、降低损失的一种基于steiner最小树的防灾型骨干网架规划方法是非常有必要的。

技术实现思路

1、本发明的目的是为了克服现有技术的不足，而提供一种综合考虑建设成本和受灾风险、增强容灾和抗灾能力、降低损失的一种基于steiner最小树的防灾型骨干网架规划方法。

2、本发明的目的是这样实现的：一种基于steiner最小树的防灾型骨干网架规划方法，所述的方法包括以下步骤：

3、步骤1：采集待规划配电网的信息，确定待规划配电网的负荷容量、负荷节点、待建负荷节点、电源节点的位置；

4、步骤2：根据待规划配电网所在位置的地理信息及历史受灾情况，确定待建线路的建设成本和电网中线路的受灾风险；

5、步骤3：建立防灾骨干网架的steiner最小树模型，steiner最小树的权重为线路的建设成本和受灾风险；

6、步骤4：用二进制粒子群算法对steiner最小树模型进行求解，得出规划方案。

7、所述的步骤1中总的负荷节点为待规划配电网中接有负荷的节点；电源节点为配电网与输电网的连接点，即配电网的主变。

8、所述的步骤s2中的电网中线路的受灾风险，根据线路的三状态天气模型确定，其具体计算步骤如下：

9、步骤2.1：采集线路的历史故障信息，即线路的停电次数及停电持续时间；

10、步骤2.2：计算线路的年平均故障率λavg，其计算方式为：式中，tf为线路的年故障持续时间；

11、步骤2.3：根据年平均故障率，计算线路的受灾风险；

12、步骤2.4：根据统计数据，假设在时间间隔δt内输电线路故障符合均匀泊松分布，则线路k在δt内的累积故障率为：pk＝1-e-λδt；

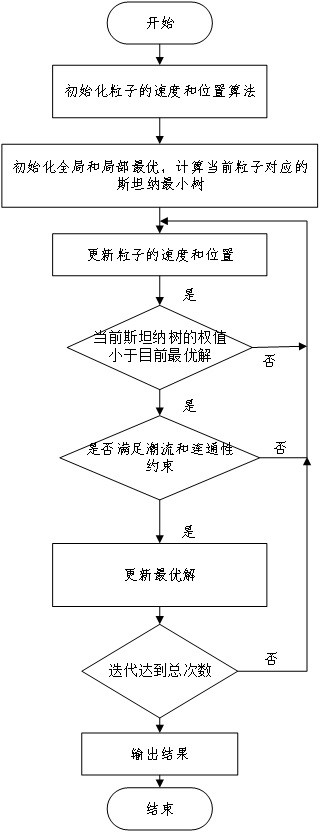
13、步骤2.5：由此可得线路的受灾风险为：rk＝pk×wk，式中，pk为线路k在δt内的累积故障率；wk为线路所带负荷的容量。

14、所述的步骤2.3中的根据年平均故障率，计算线路的受灾风险，其计算方式为：正常、恶劣和极端天气状态下输电线路的故障率可表示为如下：λn＝λavg(1-fb)/pn，λa＝λavgfb(1-fm)/pa，λm＝λavgfbfm/pm，式中：λavg为线路年平均故障率；pn、pa、pm分别为出现正常、恶劣和极端天气的稳态概率；fb为故障发生在恶劣天气的比例；fm为恶劣天气中，由极端天气引起故障的百分比；年平均故障率及以上提到的相关比率可以通过历史停运数据统计得到。

15、所述的步骤3中的防灾骨干网架的steiner最小树模型具体为：最小steiner最小树st问题是通过一系列斯坦纳点找到一棵连接所有需求节点成本最小的树，是一个经典的组合优化问题，steiner最小树问题的传统解法是一个n-p难问题，求解时间会随着斯坦纳点的规模成倍增加；因此采用边权steiner最小树，在防灾骨干网架规划中，中间节点即为斯坦纳点，权重为线路和中间节点的建设成本，防灾骨干网架规划转化为寻找电源节点通过中间节点连接到负荷节点的最小生成树；由此可以得到防灾型网架规划的数学模型为：式中，clk为线路的建设成本；rk为线路的受灾风险；对已有配电网中的线路，其建设成本为0，其权重为线路的受灾风险；对待建线路，其受灾风险为0，权重为线路的建设成本；k为平衡建设成本和建设成本的系数。

16、所述的步骤s4中的用二进制粒子群算法对steiner最小树模型进行求解的具体步骤如下：

17、步骤4.1：初始化粒子的速度和位置，粒子维数，粒子个数m，学习因子，惯性权重，粒子的最大速度，最大迭代次数；

18、步骤4.2：对每个粒子，判断其是否满足网络连通性约束和潮流约束，若满足约束，计算其适应度值，即被选入网架的所有线路的权重之和，初始化局部最优和全部最优；

19、步骤4.3：根据二进制粒子群算法的位置和速度更新公式，更新粒子的速度和位置；

20、步骤4.4：对更新后的粒子，重新判断其是否满足网络连通性约束和潮流约束，节点电压约束，若满足上述约束，计算其适应度值，更新局部最优和全部最优；

21、步骤4.5：若达到最大迭代次数，算法结束并输出结果；否则转向步骤4.3。

22、所述的步骤4.3中的粒子群算法的位置和速度更新公式为：xij(t+1)＝xij(t)+vij(t+1)，式中，pgi为粒子在飞行过程所经历过的最好位置；pij为每一个粒子搜索到的最优位置；i＝1,2,...,n，n为粒子个数；d＝1,2,...,d，d为目标搜索空间维度；c1、c2为加速因子；r1、r2为随机数，介于[0，1]之间；vij(t)、xij(t)为第t次迭代中粒子的速度和位置；sigmoid函数定义为：因此，二进制粒子群优化算法粒子位置计算式更新为下式：式中，ρij(t+1)向量的各个分量都为[0,1]之间随机产生的一个正实数。

23、所述的步骤4.4中的节点电压约束：umin,j≤uj≤umax,j式中，umax,j为节点运行时允许的最大电压值；umin,j为节点运行时允许的最小电压值；潮流约束：式中，pg,i、qg,i分别为节点j处注入的有功功率和无功功率；pl,i、ql,i为节点j处负荷的有功功率和无功功率；gj,k、bj,k为线路的电导和电纳；uj为节点j处的电压；uk为节点k处的电压；δj,k为节点j,k间的相角。

24、本发明的有益效果：本发明为一种基于steiner最小树的防灾型骨干网架规划方法，在使用中，本发明方法在保证对主要负荷供电的基础上，综合考虑了线路的建设成本和受灾风险，在保证经济性的前提下增强电网的容灾和抗灾能力，同时使配电网受灾后的损失降到最低；建立了防灾骨干网架的steiner最小树模型，同时考虑了单条线路的重要程度和整个网架的评价，利用二进制粒子群算法对模型进行求解可以求出多个解，可以做出多个备选方案，避免了只求出最优解后但实际中不可行的问题；本发明方法考虑了对骨干网架进行差异化改造的综合成本，保证电网在灾害时对重要负荷的供电，提高了电网在灾害下供电保障的能力；本发明具有综合考虑建设成本和受灾风险、增强容灾和抗灾能力、降低损失的优点。