一种基于傅里叶特征化PINN的输流管道振动分析方法

本发明属于管道振动预测，具体涉及一种基于傅里叶特征化pinn的输流管道振动分析方法。

背景技术：

1、输流管道在诸多领域中有着广泛的应用，流体在管道内流动时会对管道产生作用从而引起管道振动，最终导致管道长期疲劳失效，因此研究管道输流时的流激振动动态响应具有现实意义。然而由于输流管道中流固耦合(fluid-solid interaction,fsi)的存在，使得管道振动具有多尺度和高低频相互叠加的特性，分析管道振动变得具有挑战。因此需要开发一种算法，能够稳定地学习高频信息，同时在时空多尺度下可以准确预测具有高阶非线性项的控制方程，而不增加计算成本。

2、pinn利用神经网络普遍逼近能力，通过同时最小化数据拟合误差和偏微分方程残差之和来训练神经网络的参数，能够有效求解具有高阶非线性项的偏微分方程(pdes)。然而，由于pinn中使用的全连接架构普遍存在频谱偏差问题，使得网络在训练学习的过程中趋向于学习低频成分而忽略高频成分，难以保证正确学习高频函数。当偏微分方程的解表现出高频和多尺度特性时，pinn往往难以稳定地进行训练，并且无法产生准确的预测。

技术实现思路

1、鉴于传统深度全连接网络存在频谱偏差问题，对高频信息的学习能力不足问题，本发明提出基于傅里叶特征化pinn的输流管道振动分析方法是一种有效的解决方法，其通过将输入数据进行傅里叶映射，减缓由频率增加而导致的网络中ntk的快速下降，降低特征值随着频率的变大而衰减的程度，提高高频信息的特征值从而提高高频信息训练的收敛速度，增强全连接网络学习高频函数的能力。

2、为此，本发明提供一种基于傅里叶特征化pinn的输流管道振动分析方法。旨在建立一个能够精确有效地求解输流管道模型的数值算法，使得该算法有较强的高频学习能力，并应用于预测管道振动的变化情况。

3、该方案包括构建物理信息神经网络(pinn)，根据输流管道模型确定初始条件与边界条件，并得到其对应的损失函数；以“软”约束将第二类边界条件和管道初始激励表述到pinn损失函数中，以“硬”约束将第一类边界条件及初始振幅编码到dnn体系结构中，同时在网络中加入观测锚点，在网络模型训练过程中出现峰值不足时用以矫正；构建傅里叶特征映射γ函数，将pinn前馈神经网络输入的数据分解为空间傅里叶特征映射γ(i)(ξ)和时间傅里叶特征映射γ(j)(τ)；通过选择不同的σ值来修改傅里叶基频率向量，对网络的神经正切核进行调整，从而控制神经网络学习的频率范围；经过以上处理，将两种映射结果分别通过设置好的网络进行训练，并最后在网络中通过点乘法将空间和时间的隐藏层联系起来，建立ffnn网络；经过训练学习得到空间输出和时间输出并使用逐点乘法将两者进行合并，最后通过线性层连接输出预测结果。

4、本发明解决其技术问题具体采用的技术方案是：

5、一种基于傅里叶特征化pinn的输流管道振动分析方法，其特征在于，包括以下步骤：

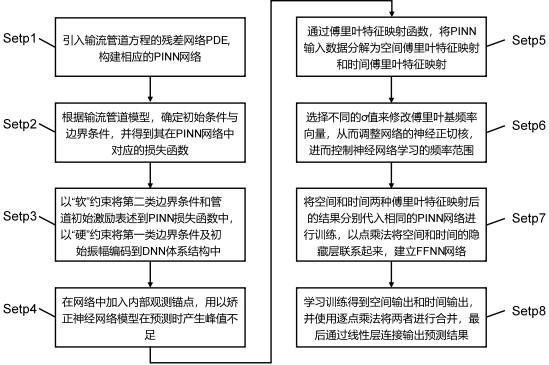
6、step1：引入输流管道方程的残差网络pde，构建相应的pinn网络；

7、step2：根据输流管道模型，确定初始条件与边界条件，并得到其在pinn网络中对应的损失函数，其中初始条件包含管道的初始振幅和初始激励，边界条件包含第一类dirichlet条件和第二类neumann条件；

8、step3：对管道问题中的一、二类边界条件及初始条件进行分开处理，以“软”约束将neumann边界条件和管道初始激励表述到pinn损失函数中，通过损失函数最小化的方式对边界条件进行约束，以“硬”约束将dirichlet边界条件及初始振幅编码到dnn体系结构中，构造满足初边值条件特解的函数，对dirichlet边界条件及初始振幅进行硬性约束；

9、step4：针对输流管道方程的高阶项和强非线性的性质，在网络中加入内部观测锚点，用以矫正神经网络模型在预测时产生峰值不足的问题；

10、step5：通过傅里叶特征映射γ函数，将pinn网络的输入数据分解为空间傅里叶特征映射γ(i)(ξ)和时间傅里叶特征映射γ(j)(τ)；

11、step6：通过选择不同的σ值修改傅里叶基频率向量，对网络的神经正切核进行调整，从而控制神经网络学习的频率范围；

12、step7：将空间和时间两种傅里叶特征映射后的结果分别代入相同的pinn网络进行训练，并在网络中通过点乘法将空间和时间的隐藏层联系起来，建立ffnn网络；

13、step8：经过训练学习得到空间输出和时间输出并使用逐点乘法将两者进行合并，最后通过线性层连接输出预测结果。

14、进一步地，步骤step1中，对于输流管道模型引入方程残差网络pde(ξ,τ)具体表达式如下：

15、

16、ηθ(ξ,τ)＝z(l)＝w(l)·a(l-1)+bl

17、式中，a为输入量，θ表示网络可学习超参数，在该网络中含权重w和偏差b，ηθ(ξ,τ)为输出向量，β为单位长度管内流体的质量占管道总质量比的无量纲分量，u为管内流速的无量纲分量，上标表示网络层数；

18、ηθ(ξ,τ)是一个l层神经网络，其输入向量a(0)(ξ,τ)t包括管道振动模型中的空间坐标ξ和时间坐标τ，输出向量为管道振幅η，该网络为前馈神经网络。

19、进一步地，步骤step2中，在软约束下第二类neumann边界条件的损失函数为：

20、

21、其初始条件即管道初始激励损失函数为：

22、

23、管道微分方程f网络的均方误差为：

24、

25、因此，软约束下的管道损失函数为：

26、l＝λiclic+λbclbc+λpdelpde

27、式中，nbc为两端固支的支撑条件时模型neumann边界条件的训练数据个数，nic为初始激励训练个数，npde为内部配置点个数，ηθ为神经网络输出，和是作为网络输入的边界条件点和初始条件点，是对应点实际的值；是传递到pde(ξ,τ)网络的配置点，参数{λic,λbc,λpde}对应于损失函数中的权重系数，以有效地为每个单独的损失项分配不同的学习率；这些权重允许由用户指定或在网络训练期间自动调整。

28、进一步地，步骤step3中，在硬约束下第一类dirichlet边界条件的损失函数为：

29、

30、其初始条件即管道初始振幅损失函数为：

31、

32、管道微分方程pde(ξ,τ)网络的均方误差为：

33、

34、因此，硬约束下的管道损失函数为：

35、

36、式中，“硬”约束构造的满足边界条件特解的函数：nbc为两端固支支撑条件时模型dirichlet边界条件的训练数据个数，nic为初始振幅训练个数，λ为对应于各项损失函数项的权重系数，下标ic、bc分别表示初始条件和边界条件。

37、进一步地，步骤step4中针对输流管道方程的高阶项和强非线性的性质，在网络中加入内部观测锚点，对应下标domain，锚点项的损失函数为：

38、

39、硬约束下加入锚点修正项的管道损失函数为：

40、

41、式中，权重λdomain取决于控制方程本身，设为0或1。

42、进一步地，步骤step5中空间傅里叶特征映射γ(i)(ξ)和时间傅里叶特征映射γ(j)(τ)表示如下：

43、

44、

45、式中，代表从高斯分布n(0,σ2)中采样得到的映射矩阵，bm表示傅里叶基频率向量，σ＞0是指定网络倾向学习频率的超参数，m为pinn网络每层神经元个数，d为网络的输入维度。

46、进一步地，步骤step6中神经正切核表示如下：

47、

48、式中，v1，v2为输入点数据。

49、进一步地，步骤step7中对于空间傅里叶特征映射γ(i)(ξ)，其网络的第一层和隐藏层分别为：

50、

51、

52、对于时间傅里叶特征映射γ(j)(τ)，其网络的第一层和隐藏层分别为：

53、

54、

55、空间和时间的隐藏层通过下式进行合并：

56、

57、式中，φ为激活函数，式中的上标表示网络层数。

58、相比于现有技术，本发明及其优选方案克服了全连接神经网络对于高频函数学习与预测的不足，结合pinn对物理信息的利用，针对输流管道模型，能够准确捕捉高频振荡，更好的学习并预测管道的振动。