融合工况与几何不确定性的翼型梯度优化设计方法

本发明涉及飞行器设计，具体涉及一种融合工况与几何不确定性的翼型梯度优化设计方法。

背景技术：

1、所有工程系统的性能都会受到某种程度的不确定性的影响。传统的气动设计属于确定性设计，有可能导致气动性能对不确定因素异常敏感，甚至会带来一定的安全隐患。因此，在飞行器设计阶段，开展考虑不确定性的鲁棒优化设计受到广泛关注。

技术实现思路

1、要解决的技术问题：

2、目前在飞行器设计阶段，目前考虑的不确定性因素主要为飞行工况的不确定性影响，但实际上，除了飞行工况的不确定性影响外，加工制造影响产生的几何不确定性因素也会导致飞行器的实际性能出现较大变化。因此，有必要融合工况与几何不确定性进行翼型优化设计，这是本发明要解决的第一个问题；

3、多项式混沌展开法以其较高的灵活性和计算效率在不确定性分析中越来越受欢迎，但目前尚应用在飞行工况不确定性影响分析这类不确定性变量维度较低的应用中，对于几何不确定性因素，由于变量维度很高，直接采用多项式混沌展开法就会存在维度灾难问题，计算成本较高，因此在不确定性分析中，如何针对高维度的几何不确定性变量进行有效选择，降低几何变量的维度，对于提高不确定性分析和优化设计的效率具有重要意义。所以有必要通过数值技术处理，进一步降低不确定性分析的计算成本，这是本发明要解决的第二个问题；

4、梯度优化算法作为一种高效的优化算法，在解决大规模设计变量气动优化设计问题中具有明显的优势，目前基于伴随的梯度优化设计方法主要应用于确定性优化设计中，而如何在不确定性分析方法中应用梯度优化算法，也是本发明要解决的问题。

5、针对上述问题，本发明提出一种融合工况与几何不确定性的翼型梯度优化设计方法，以降低飞行工况与几何不确定性对翼型性能鲁棒性的影响，且在保证求解精度的前提下大幅缩减维度，从而大大减小翼型鲁棒性优化设计过程中的计算量。

6、本发明的技术方案为：

7、所述一种融合工况与几何不确定性的翼型梯度优化设计方法，包括以下步骤：

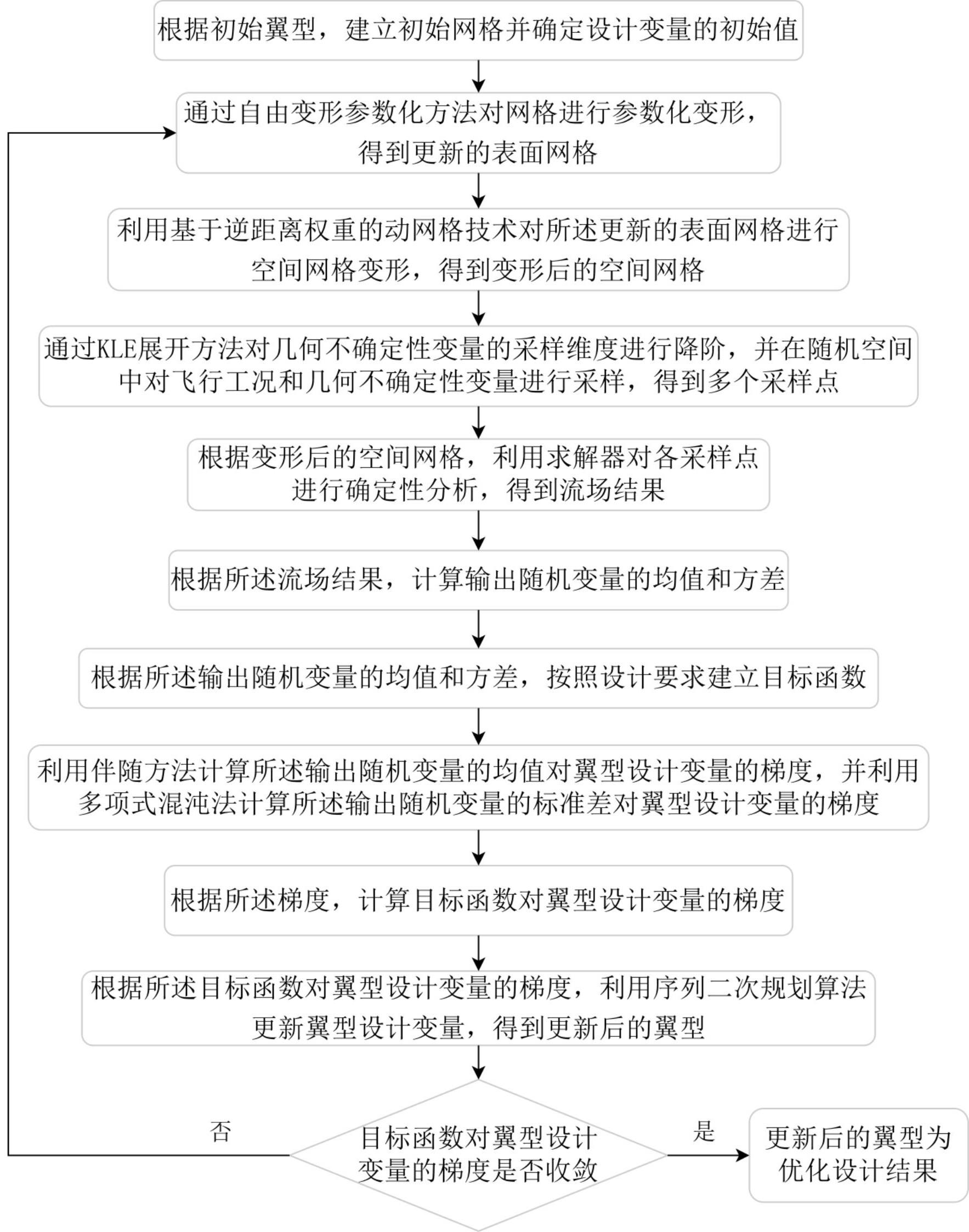
8、步骤1：根据初始翼型，建立初始网格并确定翼型设计变量的初始值，所述翼型设计变量为翼型表面控制点的位置变化量；

9、步骤2：通过自由变形参数化方法对网格进行参数化变形，得到更新后的表面网格；

10、步骤3：利用基于逆距离权重的动网格方法对所述更新后的表面网格进行空间网格变形，得到变形后的空间网格；

11、步骤4：在随机空间中对飞行工况和几何不确定性变量进行采样，得到多个采样点；其中对几何不确定性变量进行采样时，通过卡尔胡宁-洛伊夫（karhunen–loève）展开方法对采样维度进行降阶；

12、步骤5：根据步骤3得到的变形后的空间网格，利用求解器对步骤4得到的各所述采样点进行确定性分析，得到流场结果；

13、步骤6：根据步骤5得到的所述流场结果，计算输出随机变量的均值和方差；

14、步骤7：根据步骤6得到的所述输出随机变量的均值和方差，按照设计要求建立目标函数；如阻力系数的均值和标准差的加权值；

15、步骤8：利用伴随方法计算所述输出随机变量的均值对翼型设计变量的梯度，且利用多项式混沌法计算所述输出随机变量的标准差对翼型设计变量的梯度；

16、步骤9：根据步骤8得到的梯度，计算目标函数对翼型设计变量的梯度；

17、步骤10：根据步骤9得到的目标函数对翼型设计变量的梯度，利用序列二次规划算法更新翼型设计变量，得到更新后的翼型；

18、步骤11：利用步骤10得到的更新后的翼型，计算目标函数，并判断目标函数对翼型设计变量的梯度是否收敛，若是，则更新后的翼型即为优化设计结果，方法结束，否则返回步骤2。

19、进一步的，步骤3中，得到变形后的空间网格的过程为：

20、根据翼型几何参数和表面网格，计算所述表面网格中各子网格单元变化前后的法向扭转角和对应的平移距离，进而得到变形后的空间网格。

21、进一步的，步骤4中，飞行工况不确定性变量包括马赫数和迎角；几何不确定性变量为翼型表面控制点的扰动量。

22、进一步的，步骤6中，根据流场结果，对

23、

24、进行求解，得到系数，进而根据系数得到输出随机变量的均值为，输出随机变量的方差为

25、

26、表示对输出随机变量进行多项式混沌展开后的第j阶随机部分；

27、公式等号右侧中为在第一个采样点进行流场计算后得到的输出变量，为在第个采样点进行流场计算后得到的输出变量；为由翼型设计变量组成的向量；为第一个采样点中的采样向量的第一个变量，为第一个采样点中的采样向量的第n个变量，为第个采样点中的采样向量的第一个变量，为第个采样点中的采样向量的第n个变量；

28、公式等号左侧中为在第一个采样点处对输出随机变量进行多项式混沌展开后的第j阶随机部分， 为在第个采样点处对输出随机变量进行多项式混沌展开后的第j阶随机部分，j=0,1,2,…,p，p为对输出随机变量进行多项式混沌展开时进行有限模态截断的阶数；

29、表示向量中的第1个变量，由转换得到，，和分别是个采样向量中的第1个变量的均值和标准差；表示向量中的第n个变量，，和分别是个采样向量中的第n个变量的均值和标准差；

30、表示向量中的第1个变量，，表示向量中的第n个变量，；

31、表示向量中的第1个变量，，表示向量中的第n个变量，。

32、进一步的，步骤6中，对采用基于双曲线截断的稀疏化处理，降低值。

33、进一步的，所述步骤7中，

34、所述目标函数为：

35、

36、其中，和分别表示目标函数组合权重系数，为输出随机变量的标准差。

37、进一步的，步骤8中，所述输出随机变量的均值对翼型设计变量的梯度为：

38、

39、其中，表示翼型设计变量向量，为每个采样点进行流场计算后得到的输出变量对翼型设计变量的梯度；

40、所述输出随机变量的标准差对翼型设计变量的梯度为：

41、

42、其中，为多项式混沌展开系数对翼型设计变量的梯度，其中的第个元素通过求解方程

43、

44、得到，其中表示翼型设计变量组成的向量中的第个设计变量；

45、公式等号右侧中为在第一个采样点进行流场计算后得到的输出变量，为在第个采样点进行流场计算后得到的输出变量；

46、公式等号左侧中为在第一个采样点处对输出随机变量进行多项式混沌展开后的第j阶随机部分， 为在第个采样点处对输出随机变量进行多项式混沌展开后的第j阶随机部分，，为对输出随机变量进行多项式混沌展开时进行有限模态截断的阶数。

47、进一步的，所述步骤9中，所述目标函数对翼型设计变量的梯度为：

48、。

49、有益效果

50、本发明提出的融合工况与几何不确定性的翼型梯度优化设计方法，具有以下优点：

51、本发明创造性的将飞行工况不确定性与几何不确定性组合进行翼型优化设计，考虑了飞机在加工制造过程和实际飞行过程的不确定性影响，有助于提高翼型抵抗飞行工况扰动和几何不确定性扰动的能力，提升翼型平均性能和性能鲁棒性。

52、针对考虑几何不确定性因素后带来的维度灾难问题，本发明通过karhunen–loève展开方法对采样维度进行降阶，将几何不确定性变量个数从63个降低至4个，并且通过对多项式混沌展开方法进行稀疏化处理，在保证求解精度的前提下大幅缩减采样点数，从而大大提高翼型鲁棒性优化设计的效率。

53、本发明利用梯度优化设计方法有效提高计算精度并降低计算成本，从而能够在较少的计算成本下使得翼型设计结果更加符合要求。

54、本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。