基于累积故障的多任务复杂系统可靠性在役考核评估方法与流程

本发明涉及数据分析，具体地，涉及一种基于累积故障的多任务复杂系统可靠性在役考核评估方法。

背景技术：

1、高可靠的复杂系统是实现作战效能，保证任务顺利完成的基本要素之一。复杂系统可靠性水平在役考核评估可以为装备使用保障措施优化和装备设计改进提供参考。

2、伴随近一段时期复杂系统向信息化、集成化、体系化方向转变，作战任务和作战场景复杂，多任务复杂环境和多应力历程的造成任务之间可靠性水平参差不齐，此时再采用单任务假设、截尾试验统计理论进行可靠性评估往往会造成评估精度降低等问题。装备列装后在实际使用和保障条件下，经过大量的故障数据累积，使用在役考核数据评估装备可靠性更能真实反映装备真实作战水平，致使订购方更关注多任务复杂系统依据在役考核故障信息进行可靠性评估工作。针对上述情形，现阶段尚未有相应成熟的可靠性评估方法。

3、因此，市场上需要一种基于累积故障的多任务复杂系统可靠性在役考核评估方法。

技术实现思路

1、针对现有技术中的缺陷，本发明的目的是提供一种基于累积故障的多任务复杂系统可靠性在役考核评估方法。

2、根据本发明提供的一种基于累积故障的多任务复杂系统可靠性在役考核评估方法，包括：

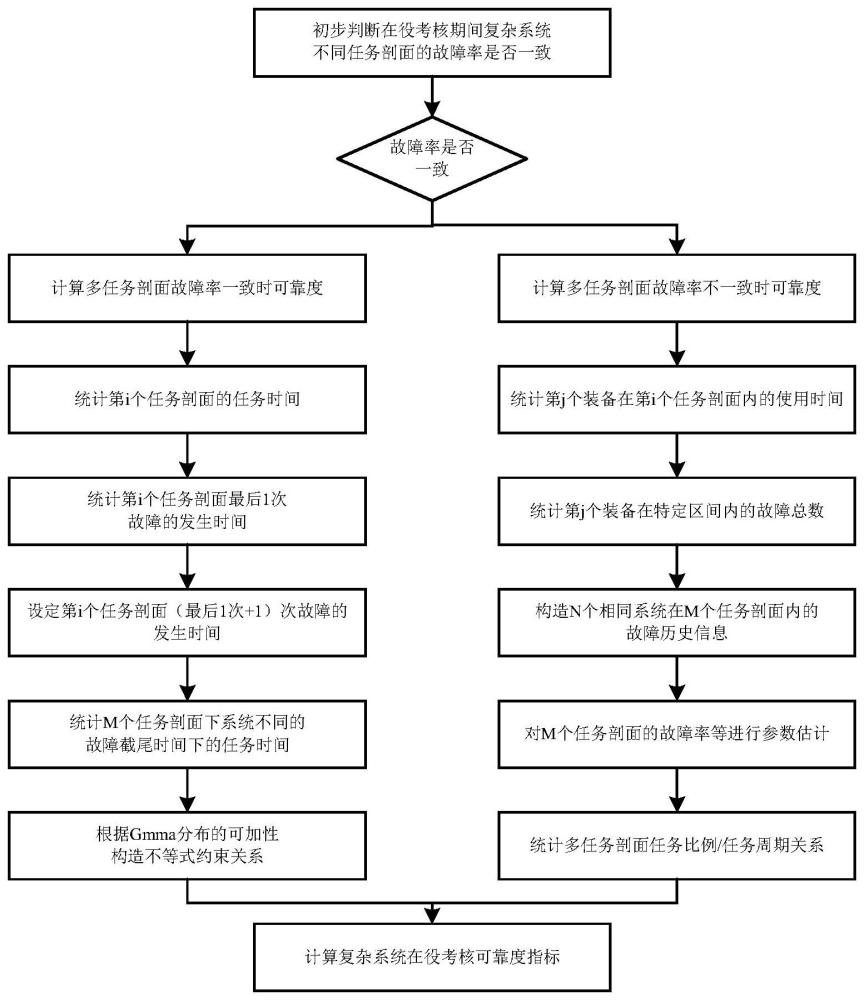
3、步骤s1：将多任务复杂系统在役考核期间不同任务剖面故障率进行拟合；

4、步骤s2：判别当前多任务剖面故障率是否一致，若是，则执行步骤s3；若否；则执行步骤s4；

5、步骤s3：计算多任务剖面故障率一致时的可靠度；

6、步骤s4：计算多任务剖面故障率不一致时的可靠度。

7、优选地，所述步骤s1包括：

8、通过故障历史信息计算复杂系统多个任务剖面下故障率水平，其中，复杂系统任一个任务剖面下故障率统计，公式如下所示：

9、

10、式中，λi表示第i个任务剖面下的故障率，ci表示在考虑的时间范围δt内，第i个任务剖面下发生的故障次数，n表示在δt内第i个任务剖面整个使用次数，δt表示考虑的时间范围，m表示任务剖面的种类数量。

11、优选地，所述步骤s2包括：

12、通过比较复杂系统在不同任务剖面下故障率，进而判断不同任务剖面下故障率是否相同，包括两种情形，具体如下：

13、情形1：多任务剖面故障率相同；其中，下标i和j分别表示m个任务剖面中第i和第j个任务剖面；

14、情形2：多任务剖面故障率不同；

15、所述任务剖面是指复杂系统在规定的使用保障条件下，完成多个任务这段时间内所经历事件按任务区分的不同时序描述。

16、优选地，所述步骤s3包括：

17、步骤s3.1：提取多任务剖面故障信息；复杂系统共计m个任务剖面，m个任务的任务周期t＝(t1,t2,…tm)，任务执行次数满足n＝(n1,n2,…,nm)，且任务执行次数比满足n1:n2:…:nm＝α1:α2:…αm；m个任务剖面发生的严重故障次数满足r＝(r1,r2,…,rm)，收集记录第i个任务剖面严重故障发生时间的顺序统计量其中1≤k≤ri；m个任务剖面的故障故障率满足λ＝(λ1,λ2,…,λm)t；

18、步骤s3.2：多任务复杂系统可靠性点估计，统计一定时间内复杂系统执行任务m个不同作战任务的总次数n，公式如下：

19、

20、式中，ni表示第i个任务执行次数。根据平均严重故障间隔时间的定义易知此时多任务剖面故障率相同时装备的任务可靠性点估计公式如下：

21、

22、

23、

24、式中，表示复杂系统任务可靠性的点估计，t0表示多任务复杂系统累积工作时长，r表示多任务复杂系统累积严重故障总数，tk表示复杂系统在执行第i个任务中发生的第k个严重故障的时间，ti表示复杂系统第i个任务剖面的任务时长；

25、步骤s3.3：多任务复杂系统可靠性区间估计，若装备第i个任务ni次任务中失效次数为ri，则装备第i个任务的截尾试验总时间，计算公式如下：

26、

27、式中，表示装备第i个任务的截尾试验总时间，ri表示复杂系统第i个任务ni次任务中失效的次数，记复杂系统第i个任务第ri次严重故障的发生时间为且记复杂系统第i个任务第ri+1次严重故障的发生时间为满足记复杂系统第i个任务分别以ti和作为截尾时间的试验总时间统计量依次为和

28、易得，计算公式分别如下：

29、

30、

31、当复杂系统m个任务均以ti和截尾时其任务总工作时间统计量分别记为tr、t0和tr+m，则tr、t0和tr+m计算公式如下：

32、

33、

34、

35、式中，表示期望特征为λ的指数分布的截尾样本的总试验时间，即

36、当多任务剖面故障率λ相同时，根据复杂系统多任务之间故障影响相互独立的假设，通过gama分布的可加性得tr、t0和tr+m均服从伽马分布，又根据gama分布和χ2分布的关系得到下面2个等式如下：

37、2tr/mtbcf～χ2(2r)

38、2tr+m/mtbcf～χ2(2r+2m)

39、当复杂系统在役考核评估规定统计模型的显著性水平或订购方风险为α时，多任务装备平均严重故障间隔时间和χ2(2r)的α下侧分位数、χ2(2r+2m)的1-α下侧分位数存在下列不等式关系如下：

40、

41、故当复杂系统多任务剖面故障率相同时，对应的平均严重故障间隔时间的区间估计计算公式如下：

42、对应的平均严重故障间隔时间的单侧置信下限计算公式如下：

43、优选地，所述步骤s4包括：

44、步骤s4.1：多任务剖面故障信息提取，若复杂系统遂行多任务且多任务之间使用环境差异大，不同任务间表现为故障率不同时，采用解析法给出装备多任务可靠性评估模型；

45、记录复杂装备在规定的时间内进行的试验故障数据，且以装备为单位进行多任务故障数据的统计，合计共有n个装备参与试验数据统计，记第j个复杂系统在m个任务内的任务总有效时间tj＝(tj1,tj2,…,tjm)；若第j个复杂系统在第i个任务内没有执行任务，则tji＝0；若第j个复杂系统在第i个任务内多次执行任务，则tji为试验截尾时间之和；记第j个复杂系统统计时间内的严重故障总数为fj，则n个装备的故障总数f满足f＝(f1,f2,…fn)t；记m个任务剖面故障率λ＝(λ1,λ2,…,λm)t；记第j个复杂系统m个任务内的故障信息为(tj,λ,fj)，得到第j个复杂系统任务总有效时间，m个任务剖面故障率和第j个复杂系统统计时间内的严重故障总数fj之间的关系计算公式如下：

46、

47、式中，εj为均值为0，方差为1的白噪声；

48、若a＝(t1,t2,…tn)t，ε＝(ε1,ε2,…,εn)t，上式可扩展为满足n个复杂系统故障信息下的矩阵方程a·λ＝f+ε，计算公式如下：

49、

50、复杂系统在役考核长时间故障累积的情况下，易知a和f，且复杂系统数量n大于多任务剖面数量m时，即a的行数大于列数，非齐次线性方程组a的秩等于其增广矩阵的秩，由gauss-markov定理得复杂系统m个任务其故障率λ的估计，计算公式如下：

51、

52、式中，σ2的无偏估计为当订购方风险为α时，复杂系统第i个任务的故障率置信区间满足其故障率单侧置信上限为ci为(ata)-1的第i个对角线元素，μ为标准正态分布下侧分位数；

53、步骤s4.2：多任务复杂系统可靠性点估计。易知，此时多任务剖面故障率相同时装备的任务可靠性点估计上式中，

54、步骤s4.3：多任务复杂系统可靠性区间估计，根据复杂系统第i个任务剖面的故障率单侧置信上限为第i个任务剖面平均严重故障间隔时间的单侧置信下限计算公式如下：

55、

56、若已知复杂系统任务比，当复杂系统多任务剖面故障率不同时，复杂系统平均严重故障间隔时间单侧置信下限近似值计算公式如下：

57、

58、根据本发明提供的一种基于累积故障的多任务复杂系统可靠性在役考核评估系统，包括：

59、模块m1：将多任务复杂系统在役考核期间不同任务剖面故障率进行拟合；

60、模块m2：判别当前多任务剖面故障率是否一致，若是，则执行模块m3；若否；则执行模块m4；

61、模块m3：计算多任务剖面故障率一致时的可靠度；

62、模块m4：计算多任务剖面故障率不一致时的可靠度。

63、优选地，所述模块m1包括：

64、通过故障历史信息计算复杂系统多个任务剖面下故障率水平，其中，复杂系统任一个任务剖面下故障率统计，公式如下所示：

65、

66、式中，λi表示第i个任务剖面下的故障率，ci表示在考虑的时间范围δt内，第i个任务剖面下发生的故障次数，n表示在δt内第i个任务剖面整个使用次数，δt表示考虑的时间范围，m表示任务剖面的种类数量。

67、优选地，所述模块m2包括：

68、通过比较复杂系统在不同任务剖面下故障率，进而判断不同任务剖面下故障率是否相同，包括两种情形，具体如下：

69、情形1：多任务剖面故障率相同；其中，下标i和j分别表示m个任务剖面中第i和第j个任务剖面；

70、情形2：多任务剖面故障率不同；

71、所述任务剖面是指复杂系统在规定的使用保障条件下，完成多个任务这段时间内所经历事件按任务区分的不同时序描述。

72、优选地，所述模块m3包括：

73、模块m3.1：提取多任务剖面故障信息；复杂系统共计m个任务剖面，m个任务的任务周期t＝(t1,t2,…tm)，任务执行次数满足n＝(n1,n2,…,nm)，且任务执行次数比满足n1:n2:…:nm＝α1:α2:…αm；m个任务剖面发生的严重故障次数满足r＝(r1,r2,…,rm)，收集记录第i个任务剖面严重故障发生时间的顺序统计量其中1≤k≤ri；m个任务剖面的故障故障率满足λ＝(λ1,λ2,…,λm)t；

74、模块m3.2：多任务复杂系统可靠性点估计，统计一定时间内复杂系统执行任务m个不同作战任务的总次数n，公式如下：

75、

76、式中，ni表示第i个任务执行次数，m表示任务剖面的种类数量。根据平均严重故障间隔时间的定义易知此时多任务剖面故障率相同时装备的任务可靠性点估计公式如下：

77、

78、

79、

80、式中，表示复杂系统任务可靠性的点估计，t0表示多任务复杂系统累积工作时长，r表示多任务复杂系统累积严重故障总数，tk表示复杂系统在执行第i个任务中发生的第k个严重故障的时间，ti表示复杂系统第i个任务剖面的任务时长；

81、模块m3.3：多任务复杂系统可靠性区间估计，若装备第i个任务ni次任务中失效次数为ri，则装备第i个任务的截尾试验总时间，计算公式如下：

82、

83、式中，表示装备第i个任务的截尾试验总时间，ri表示复杂系统第i个任务ni次任务中失效的次数，记复杂系统第i个任务第ri次严重故障的发生时间为且记复杂系统第i个任务第ri+1次严重故障的发生时间为满足记复杂系统第i个任务分别以tri、ti和作为截尾时间的试验总时间统计量依次为和

84、易得，计算公式分别如下：

85、

86、

87、当复杂系统m个任务均以ti和截尾时其任务总工作时间统计量分别记为tr、t0和tr+m，则tr、t0和tr+m计算公式如下：

88、

89、

90、

91、式中，表示期望特征为λ的指数分布的截尾样本的总试验时间，即

92、当多任务剖面故障率λ相同时，根据复杂系统多任务之间故障影响相互独立的假设，通过gama分布的可加性得tr、t0和tr+m均服从伽马分布，又根据gama分布和χ2分布的关系得到下面2个等式如下：

93、2tr/mtbcf～χ2(2r)

94、2tr+m/mtbcf～χ2(2r+2m)

95、当复杂系统在役考核评估规定统计模型的显著性水平或订购方风险为α时，多任务装备平均严重故障间隔时间和χ2(2r)的α下侧分位数、χ2(2r+2m)的1-α下侧分位数存在下列不等式关系如下：

96、

97、故当复杂系统多任务剖面故障率相同时，对应的平均严重故障间隔时间的区间估计计算公式如下：

98、对应的平均严重故障间隔时间的单侧置信下限计算公式如下：

99、优选地，所述模块m4包括：

100、模块m4.1：多任务剖面故障信息提取，若复杂系统遂行多任务且多任务之间使用环境差异大，不同任务间表现为故障率不同时，采用解析法给出装备多任务可靠性评估模型；

101、记录复杂装备在规定的时间内进行的试验故障数据，且以装备为单位进行多任务故障数据的统计，合计共有n个装备参与试验数据统计，记第j个复杂系统在m个任务内的任务总有效时间tj＝(tj1,tj2,…,tjm)；若第j个复杂系统在第i个任务内没有执行任务，则tji＝0；若第j个复杂系统在第i个任务内多次执行任务，则tji为试验截尾时间之和；记第j个复杂系统统计时间内的严重故障总数为fj，则n个装备的故障总数f满足f＝(f1,f2,…fn)t；记m个任务剖面故障率λ＝(λ1,λ2,…,λm)t；记第j个复杂系统m个任务内的故障信息为(tj,λ,fj)，得到第j个复杂系统任务总有效时间，m个任务剖面故障率和第j个复杂系统统计时间内的严重故障总数fj之间的关系计算公式如下：

102、

103、式中，εj为均值为0，方差为1的白噪声；

104、若a＝(t1,t2,…tn)t，ε＝(ε1,ε2,…,εn)t，上式可扩展为满足n个复杂系统故障信息下的矩阵方程a·λ＝f+ε，计算公式如下：

105、

106、复杂系统在役考核长时间故障累积的情况下，易知a和f，且复杂系统数量n大于多任务剖面数量m时，即a的行数大于列数，非齐次线性方程组a的秩等于其增广矩阵的秩，由gauss-markov定理得复杂系统m个任务其故障率λ的估计，计算公式如下：

107、

108、式中，σ2的无偏估计为当订购方风险为α时，复杂系统第i个任务的故障率置信区间满足其故障率单侧置信上限为ci为(ata)-1的第i个对角线元素，μ为标准正态分布下侧分位数；

109、模块m4.2：多任务复杂系统可靠性点估计。易知，此时多任务剖面故障率相同时装备的任务可靠性点估计上式中，

110、模块m4.3：多任务复杂系统可靠性区间估计，根据复杂系统第i个任务剖面的故障率单侧置信上限为第i个任务剖面平均严重故障间隔时间的单侧置信下限计算公式如下：

111、

112、若已知复杂系统任务比，当复杂系统多任务剖面故障率不同时，复杂系统平均严重故障间隔时间单侧置信下限近似值计算公式如下：

113、

114、与现有技术相比，本发明具有如下的有益效果：

115、1、本发明利用多任务复杂系统历史故障信息对其可靠性水平进行定量分析的目的，符合工程上的现实需求，同时解决了复杂情形下多任务复杂系统可靠性评估问题，并且可靠性评估结果具有可信性。

116、2、本发明提供的评估方法计算简单，方便工程技术人员使用，具有很强的应用价值。