基于多识别等级标签的多分类多目标跟踪算法评价方法与流程

本发明涉及信号处理，尤其涉及一种基于多识别等级标签的多分类多目标跟踪算法评价方法。

背景技术：

1、通过多个异构传感器进行多目标跟踪在自动驾驶、路口监控、海事及空天监控等领域有着广泛的应用。类似于在单目标跟踪问题中表征目标真实和估计状态间偏差的欧氏距离和马氏距离等向量度量，在多目标跟踪问题中，表征多目标状态的有限集间的距离度量定义也具有重要意义。其中，距离度量概念代表了满足数学意义上具有非负性、对称性、不可分辨之同一性和三角形不等式性质的有限集上的距离函数。在多目标跟踪问题中，以一个定义良好的距离度量作为评价指标在以下几个方面具有重要意义：

2、(1)性能评估。评价准则作为衡量标准可以给出不同算法给出的估计值和真实值之间的偏差距离，以评估算法的性能。

3、(2)算法估计准则。距离度量可以被视为从目标状态随机有限集的后验概率密度中得出最优估计值的准则，例如多目标跟踪中的经典方法：最小化平均最优子模式分配(ospa)方法。

4、(3)传感器管理。得益于有限集度量在优化时关键的多对多一致性优点，表示多目标状态的有限集间的距离度量在多传感器-多目标传感器视场指向管理中具有重要的应用价值。

5、(4)定义度量空间。根据有限集空间上的距离度量定义可以导出度量空间这一概念，基于此才能严格地分析估计器的收敛性，或直接在有限集上做最近邻搜索、聚类和分类操作。

6、多目标跟踪算法的性能评估是一个由来已久的研究方向，涉及许多领域。其评价指标既有符合距离度量定义的，也有不满足的。考虑到距离度量在数学意义上的一致性在性能评估中不可或缺的重要性，在此重点回顾那些符合距离度量定义的评价指标，并简要回顾几个广泛用于多目标跟踪研究领域的指标。有限集上的hausdorff距离是第一个应用于多目标跟踪的距离度量。由于hausdorff距离对有限集的势差异不敏感，并且对状态点的异常值过于敏感，因此受有限集分布之间的wasserstein距离启发，提出了最优质量转移(omat)度量。然而，简单地通过归一化来平衡不相等的有限集的势来构造分布函数，有时会导致omat度量出现反直觉的结果。而ospa通过将"虚点"引入有限集来平衡势的差异，并且约束势差异惩罚项，得到了一种比前者更符合直觉的距离度量来作为评价指标。在此基础上提出的广义ospa(gospa)和完备ospa(cospa)，避免最优ospa估计器中的"幽灵效应"，并且完善了ospa度量家族。此外，还提出了一些基于ospa度量的补充指标，如关注不确定性的hellinger-ospa，在ospa中加入质量因子的q-ospa，针对分层有限集的多组群ospa，以及适应视觉任务中引入边界框的iou-ospa等评价指标。由于ospa度量广泛的有效性，还出现了用于轨迹有限集空间的距离度量和用于slam领域的距离度量等等，这些都大大丰富了距离度量作为评价指标的应用范围。

7、随着近年来深度学习、边缘计算和传感器技术的快速发展，在需求侧和方法侧两端，多目标跟踪解决方案都倾向于通过融合来自多个异构传感器的多类信息来获得更优的估计结果。一方面，多目标跟踪的应用场景越来越多样化，比如通过融合多视角视觉和v2x信息来追踪十字路口的汽车、自行车和行人，或者在天基海事监控中通过光学/sar图像和ais信息来追踪各种船只。上述场景的一个共同特点是，信息是由不同类型的传感器收集的，通常由于传感器的感知原理及分辨率不同，在对目标进行检测识别后，结果具有多种层次的类别标签信息。例如，v2x和ais中带有的目标信息由于来自合作目标，总是具有id号码来区分个体，例如船舶的mmsi号码，这便是归于个体层面的精确信息。而从光学/sar图像中经过检测和分类步骤后得到的目标信息就不会如此精确，取决于分辨率和分类器本身的精细程度，仅可判别出不同级别(颗粒度)的类别标签信息。另一方面，联合跟踪与分类方法越来越受到关注。所有这些动机都表明我们需要一个一致的评价指标，能够以统一的标准评估同时带有状态和类别信息的有限集之间的差异距离，并且这个评价指标符合直觉且可解释，能够同时捕捉到有限集的势误差、状态误差和错误分类造成的差异。然而，目前还没有一个广泛使用的，既在数学上严格为距离度量，且同时满足上述所有需求的评价指标。针对多类多目标跟踪算法的性能评价方法，传统的最优子模式分配(ospa)度量评价方法通常为每一类目标单独计算一个评价值，或者附加引入分类错误率等其他指标，这就降低了ospa作为一个综合性单一指标的价值。一种由目标动力学状态x和类别标签c组成的(x,c)空间上的omat度量的启发式扩展，其基距离为其中代表类别标签c映射在欧几里得空间中的某个点的坐标。然而，这一评价指标并没有被进一步深入研究，也不能被用在多识别等级的类别标签情形中。此外，可通过引入联合概率散度(jpd)来同时量化跟踪误差、错误分类以及它们之间的相互依赖关系。然而，这个指标并不满足数学上距离度量的定义，也没有得到广泛的使用。

8、因此，解决多分类多目标跟踪算法的评价问题，在自动驾驶、路口监控、海事及空天监控等领域，具有重要的实际应用意义。

技术实现思路

1、为解决上述现有技术中存在的技术问题，本发明的目的在于提供一种的基于多识别等级标签的多分类多目标跟踪算法评价方法，可用于层次化多识别等级分类下的多类多目标跟踪问题，并提出了相应的评价准则，能够综合衡量多类多目标跟踪问题中目标状态误差、势误差和错误分类造成的估计偏差。

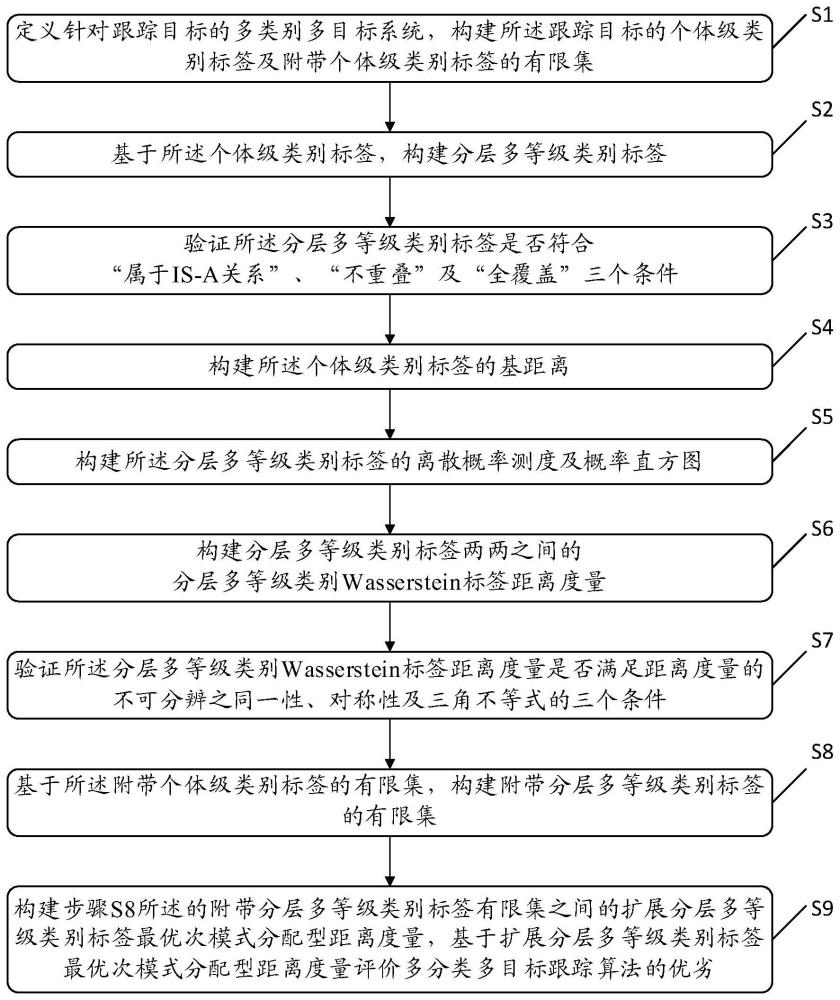
2、为实现上述发明目的，本发明提供一种基于多识别等级标签的多分类多目标跟踪算法评价方法，包括以下步骤：

3、步骤s1、定义针对跟踪目标的多类别多目标系统，构建所述跟踪目标的个体级类别标签及附带个体级类别标签的有限集；

4、步骤s2、基于所述个体级类别标签，构建分层多等级类别标签；

5、步骤s3、验证所述分层多等级类别标签是否符合“属于is-a关系”、“不重叠”及“全覆盖”三个条件；

6、步骤s4、构建所述个体级类别标签的基距离；

7、步骤s5、构建所述分层多等级类别标签的离散概率测度及概率直方图；

8、步骤s6、构建分层多等级类别标签两两之间的分层多等级类别wasserstein标签距离度量；

9、步骤s7、验证所述分层多等级类别wasserstein标签距离度量是否满足距离度量的不可分辨之同一性、对称性及三角不等式的三个条件；

10、步骤s8、基于所述附带个体级类别标签的有限集，构建附带分层多等级类别标签的有限集；

11、步骤s9、构建步骤s8所述的附带分层多等级类别标签有限集之间的扩展分层多等级类别标签最优次模式分配型距离度量，基于扩展分层多等级类别标签最优次模式分配型距离度量评价多分类多目标跟踪算法的优劣。

12、根据本发明的一个技术方案，在所述步骤s1中，具体包括：

13、对于所述多类别多目标系统，各个目标带有唯一身份且固定不变，所述多类别多目标系统的状态可被形式化为一个带标记有限集，则有：

14、

15、其中，|x|代表有限集x的势，即目标的数量；

16、令单个目标的状态空间表示为笛卡尔积目标状态其中，实数向量为目标的运动学状态，则为所谓的个体级标签，代表此目标的唯一身份，在一个离散有限空间中取值。

17、根据本发明的一个技术方案，所述步骤s2中，所述分层多等级类别标签所代指的集合c，符合树状分层分类结构，具体包括：

18、步骤s21、在树状的层次结构的根节点上，将所有的原始信号集合分成目标集合和非目标集合

19、步骤s22、目标集根据不同颗粒度分类器的识别能力及设定，分层次地划分为多个子集，直到个体层次，所有层次上的每个标签都表示一个从有限数量目标集合中划分出来的子集，用h＝1,...,h区分分类的层次级别，即分类树的深度，记c(h)为一个属于第h级的类别标签，代指一个从中抽取的集合。

20、根据本发明的一个技术方案，在所述步骤s3中，

21、属于is-a关系表示为：所有以所述分层多等级类别标签c表示的类别概念，满足非对称性、反自反性、传递性的类别分类学关系；

22、不重叠表示为：对于任意两个同级别的类别集合两两不相交

23、全覆盖表示为：对于任一以第h级标签c(h)代指的类别集合，其叶子子集需满足此外，对于所有h级同级标签c(h)表示的集合，其并集覆盖整个身份空间

24、根据本发明的一个技术方案，在所述步骤s4中，具体包括：

25、定义个体级类别标签的基距离，记为dg(·)；

26、将所有的个体级类别标签嵌入一个欧氏空间，然后用嵌入点坐标间的某一种距离度量作为标签的距离；或

27、将高层级类别标签嵌入一个欧几里得空间；

28、将同一类别中的每一个个体级标签嵌入至扩展维度中，与高维单纯形的顶点相关联。

29、根据本发明的一个技术方案，在所述步骤s5中，具体包括：

30、假设关注的目标集元素有一个初始的先验分布，称为缺省分布；

31、将其表示为概率直方图(或概率向量)取值于概率单纯形，表示为：

32、

33、其中，为概率直方图或概率向量，为目标属于个体级标签ci所代表类别的概率，为类别标签的数量；

34、分层多等级类别标签c的离散概率测度记为：

35、

36、其中，为固连于个体级标签ci的dirac单位脉冲函数；

37、则类别标签c的概率直方图便可表示为概率向量pc，

38、

39、其中，对角矩阵1c是一个指示器，即当ci∈c时，1ci,i＝1；否则，1ci,i＝0。

40、根据本发明的一个技术方案，在所述步骤s6中，具体包括：

41、令c1＝{c1,...,cm}和c2＝{c′1,...,c′n}为同一颗分类树上的任意两个分层多等级类别标签，即

42、分层多等级类别标签c1,c2的离散概率测度分别依照直方图向量通过所述步骤s5定义；

43、给定度量空间和基距离dg，其中为个体级标签空间，dg为所述步骤s4定义的基距离，则分层多等级类别标签c1,c2的hmc-距离定义为如下的一阶wasserstein距离，

44、

45、下极限取自遍历有效传输计划集合中所有的m×n传输矩阵的极小值，则有：

46、

47、记最优传输计划为则分层多等级类别标签距离可写作：

48、

49、其中，dg(ci，cj)为所述步骤s4定义的类别标签ci，cj间的基距离，为与类别标签ci，cj对相对应的最优传输计划。

50、根据本发明的一个技术方案，所述步骤s7中，具体包括：

51、令实数向量表示单一目标的状态向量，并定义有限集x＝{x1，...，xn}为一组有限数量个向量组成的集合，与相同数量目标的状态相对应，其中，数量n被称作有限集x的势，且这里的为单一目标状态空间的所有子集组成的集合；

52、令为具有任意势数量的任意三个有限集，当非负函数时，验证满足下面三项条件即可称其为有限集的一种距离度量：

53、验证不可分辨之同一性表示为：d(x，y)＝0当且仅当x＝y；

54、验证对称性表示为：d(x，y)＝d(y，x)对于所有的均成立；

55、验证满足三角不等式表示为：d(x，y)≤d(x，z)+d(z，y)对于所有的均成立。

56、根据本发明的一个技术方案，所述步骤s8中，具体包括：

57、根据所述步骤s1中的所述个体级标签及附带标签的有限集x，构建附带分层多等级类别标签的有限集，则所述多目标系统的附带类别标签的观测值表示为：

58、

59、

60、其中，|x|为目标集合中目标的数量，xi，ci分别为目标i的位置状态和类别标签。

61、根据本发明的一个技术方案，所述步骤s9中，具体包括：

62、对于最优次模式分配类型的度量，基本的归一化/非归一化最优次模式分配距离和广义最优次模式分配距离，选择两个有限集中元素之间的距离为度量，得到数学意义上的度量。

63、本发明与现有技术相比，具有如下有益效果：

64、本发明提出了一种基于多识别等级标签的多分类多目标跟踪算法评价方法，基于分层多级类标签扩展了传统最优子模式分配度量评价方法，分层多等级类别标签可作为基于层次化树状结构分类学分类后的目标有限集的附属标签，通过在任意两个标签所代表的类别分布之间定义一个类wasserstein距离度量，得到了一种满足数学定义的距离度量作为多分类多目标跟踪算法评价方法，能够应用于层次化多识别等级分类下的多类多目标跟踪问题，并提出了相应的评价准则，能够综合衡量多类多目标跟踪问题中目标状态误差、势误差和错误分类造成的估计偏差，推广应用至评价自动驾驶、智慧路口等场景的多目标跟踪算法，具有重要的实际应用意义。