基于固定时间时变神经动力学优化的稀疏信号重构方法

本发明涉及信号重构，尤其涉及一种基于固定时间时变神经动力学优化的稀疏信号重构方法。

背景技术：

1、稀疏重建广泛应用于信号处理、目标检测、雷达探测、电子工程等领域，并在工程和科学界引起了相当大的兴趣。其目的是从有噪声的欠定线性系统中估计未知稀疏信号。与采用nyquist采样定理方法相比，基于压缩感知原理的稀疏重构过程包含重构原始信息所需的全部信息的条件下，其采样速度更低，原理图如图1所示。从理论和实际应用角度分析，提出高效的稀疏重构算法是稀疏重建研究中关键问题之一。

2、近年来，大量的稀疏优化问题建立在大数据的基础之上，并且对数据处理的实时性要求越来越高，比如在卫星通信中，当拍摄的视频图像从卫星传输到地面终端，需要经过短时间的降噪去处理之后，才能呈现在科研人们面前；又如在搜索引擎中，输入关键字后，需要在毫秒级的时间内显示出搜索结果。如今，随着数据的种类越来越多，维度越来越高，迫切需要开发一类高效的优化算法求解稀疏优化问题。现有的数值优化算法，收敛速度较慢且实时性不强。例如，申请号为2009100237853的中国发明专利文献[1]，发明名称为一种稀疏信号的重构方法；申请号为201210290161x的中国发明专利文献[2]，发明名称为一种稀疏采样与信号压缩感知重构方法。收敛速度快、计算精度高、抗干扰能力强是设计高效优化算法的重要指标。不同于迭代优化方法和智能优化方法，神经动力学优化算法利用神经元的活动机制实现信息的并行处理，同时lyapunov稳定性理论为神经动力学优化算法的动力学特性研究提供了统一的分析框架。神经动力学优化算法是通过研究大脑处理信息的过程而抽象出来的数学方法，同时也是当前人工神经网络领域的研究热点和重要分支。神经动力学优化算法具备并行计算性、快速收敛性、可解释性、强实时性和物理实现性等优势，在材料科学、数据科学和信息科学等领域发挥着重要作用。作为一类并行算法，在神经动力学模型中，一个变量对应于一个神经元，且变量随时间演化，产生的状态轨迹是连续的，且最终收敛到问题的解。目前有一些渐进收敛或者指数收敛的神经动力学优化算法处理稀疏信号重构问题。例如，申请号为20211100950377的中国发明专利文献[3]，发明名称为一种基于ipnn和压缩感知的稀疏信号重构方法；发表在ieee transactions on signalprocessing期刊上的文献[4]，题目为discrete and continuous-time soft-thresholding for dynamic signal recovery；发表在neural processing letters期刊上的文献[5]，题目为solving mixed variational inequalities via a proximalneurodynamic network with applications；为进一步提高神经动力学算法的收敛速度，有限时间算法被研究。例如，发表在signal processing期刊上的文献[6]，题目为dynamical sparse signal recovery with fixed-time convergence；有限时间神经动力学算法的收敛时间上界往往与算法的初始状态相关，因此有相关学者研究基于神经动力学优化的与初始状态无关的稀疏信号重构方法。例如，发表在ieee signal processingletters期刊上的文献[7]，题目为cappa:continuous-time accelerated proximal pointalgorithm for sparse recovery；发表在ieee transactions on cybernetics期刊上的文献[8]，题目为a novel fixed-time converging neurodynamic approach to mixedvariational inequalities and applications；

3、现有的稀疏信号重构方法可能存在以下问题和缺陷。首先，现有数值迭代方法大多是基于数字计算机实现(如文献[1,2])，不利于算法的实时性刻画；其次，现有神经动力学算法大多是渐进收敛或指数收敛，理论上当时间趋于无穷时，神经动力学优化方法的轨迹实现完整的稀疏信号重构目标(如文献[3，4，5])；再者，有限时间稀疏信号重构算法(如文献[6])的收敛时间上界与初始状态相关，在一些情况下，系统的初始状态可能是未知的，不利于收敛时间上界的刻画；固定时间稀疏信号重构算法(如文献[7，8])的增益系数是常数，不能实现算法的自适应步长调节。

技术实现思路

1、本发明提供一种基于固定时间时变神经动力学优化的稀疏信号重构方法，目的在于给出了稀疏信号重构的时间上界，通过调节相关时变系数，具有较快的收敛速度。

2、为实现上述目的，本发明提供如下技术方案：

3、一种基于固定时间时变神经动力学优化的稀疏信号重构方法，包括以下步骤：

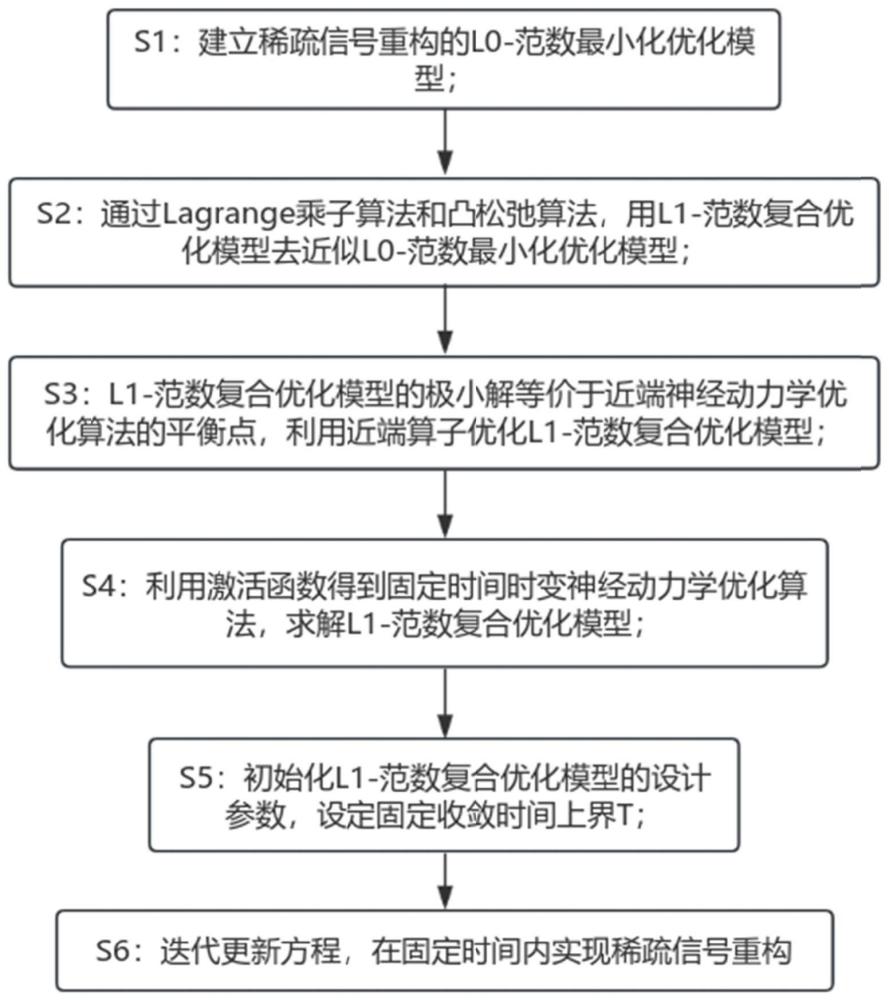
4、步骤s1：建立稀疏信号重构的l0-范数最小化优化模型；

5、步骤s2：通过lagrange乘子算法和凸松弛算法，用l1-范数复合优化模型去近似l0-范数最小化优化模型；

6、步骤s3：l1-范数复合优化模型的极小解等价于近端神经动力学优化算法的平衡点，利用近端算子优化l1-范数复合优化模型；

7、步骤s4：利用激活函数得到固定时间时变神经动力学优化算法，求解l1-范数复合优化模型；

8、步骤s5：初始化l1-范数复合优化模型的设计参数，设定固定收敛时间上界t；

9、步骤s6：迭代更新方程，在固定时间内实现稀疏信号重构。

10、优选的，步骤s1中，所述l0-范数最小化优化模型为：

11、

12、式中，为欲重构的信号数据；矩阵为测量矩阵；为观测矩阵；为n维实数欧几里得空间；||x||0为0范数用来计算向量x中的非零元素个数，σ>0为正则化参数，用以权衡估计信号的精确度和稀疏度。

13、优选的，步骤s2中，所述l1-范数复合优化模型为：

14、

15、其中，

16、

17、式中，γ(x)＝σ||x||1，η>0是一个可调常系数步长，σ>0是一个正则化参数，proxηυ(·)为近端算子。

18、优选的，步骤s3中，所述近端神经动力学优化算法的计算表达式为：

19、

20、其中，

21、

22、

23、式中，ρ>0为一个可调参数。

24、公式(6)具有渐进指数收敛性质，表明当时间t趋于无穷时，x(t)收敛到l1-范数复合优化模型的最优解，实现了稀疏信号重构。

25、优选的，步骤s4中的激活函数为：

26、

27、式中，1>ξ1>0和ξ2>1为两个可调参数；

28、通过所述固定时间时变神经动力学优化算法，求解稀疏信号重构：

29、

30、其中，

31、

32、

33、式中，为两个连续函数。

34、时变神经动力学优化算法(公式7)具有固定时间收敛性质，并且时变神经动力学优化算法(公式7)与近端神经动力学优化算法(公式6)的平衡点等价，因此求解l1-范数复合优化模型等价于求解时变神经动力学优化算法(公式7)的平衡点。

35、优选的，步骤s5中，假设测量矩阵ψ满足2s限制等距条件rip，并且ηl2<2μ，公式(7)的轨迹在固定时间内收敛到最优解x*，所述固定收敛时间上界t满足以下表达式：

36、

37、其中，为四个常数；

38、

39、

40、μ为强单调系数。

41、式中，γ为时间；t为总步长；l为lipschitz常数；

42、优选的，由于时变神经动力学优化算法是连续的，因此需要进行离散化处理，包括以下步骤：

43、当迭代次数k≤[γ/δt]+1时，总步长t＝kδt，计算求解

44、更新步骤：

45、

46、k＝k+1；

47、式中，k为迭代次数，初始值为0；δt为步长。

48、与现有技术相比较，本发明具有如下有益效果：

49、本发明不同于一般的渐近收敛或指数收敛的优化算法，本方法给出了稀疏信号重构的时间上界；

50、其次，区别于一般的稀疏信号重构的固定时间方法，本方法通过调节相关时变系数，具有较快的收敛速度。