一种多台线激光传感器坐标系相对于转轴的标定方法与流程

本发明属于自动检测，特别提供一种针对多台线激光传感器坐标系相对于转轴标定的方法。

背景技术：

1、大型回转体零件的尺寸测量需求广泛存在于众多工业领域，包括航空航天、汽车制造、船舶制造、风能和冶金行业等。这些领域中，大型回转体零件如引擎部件、齿轮箱、轴承座、风力涡轮机组和冶金车轮等，起到至关重要的作用。以冶金行业为例，车轮铸造过程中，尤其是热态车轮的关键尺寸高精度测量显得格外重要。这不仅有助于提高成材率和成品率，还确保了车轮在运行中的安全性和性能。从行业需求的角度出发，尺寸测量在确保产品质量、合规性和性能方面发挥着关键作用，特别是在大型回转体零件的制造和运用中，其重要性不言而喻。

2、传统的测量方法依赖于经验丰富的专业工人使用卡具进行热态车轮尺寸测量，然而，这种方法存在一些显著的不足。首先，这种传统方法效率较低，且只能测量车轮的部分截面的关键尺寸，无法提供全面的数据。其次，测量精度受到许多因素的影响，包括工人师傅的熟练程度以及测量工具本身的精度。这种依赖人工技能的方法经常导致检测精度不稳定，难以满足质量控制的高标准。因此，寻求更高效、准确和可靠的测量方法对于冶金行业中热态车轮的制造至关重要。

3、光学测量技术，包括激光测距仪、光学传感器和相机，为非接触式测量提供了高分辨率的数据，但对表面质地和光照条件敏感，光路清晰性可能需要复杂的设置。激光雷达系统适用于大范围测量，但成本较高，对透明材料存在限制。三坐标测量机提供高精度，但昂贵且需要专业操作。超声波测量在某些材料和环境条件下可能不够准确。机器学习方法有潜力提高测量速度和准确性，但需要大量训练数据，可能受到噪声和环境变化的干扰。

4、激光传感器是一种广泛应用于测距、三维成像和定位的高精度传感器。多台线激光传感器系统是一种由多个激光传感器组成的系统，用于捕捉目标物体的三维信息。这些系统常用于三维扫描、质量控制等应用中，因为它们能够提供高分辨率和高精度的数据。

5、在实际应用中，多台线激光传感器系统需要进行相机坐标系标定和转轴标定，以确保各个传感器的数据能够准确对齐并在设定的世界坐标系下保持一致。本发明采用自主设计的圆柱异形标靶，通过各台传感器采集数据的特征点，实现了多相机坐标系相对于转轴所在的世界坐标系的标定，解决了多线激光传感器系统的标定难题。

技术实现思路

1、本发明目的在于提供一种多台线激光传感器坐标系相对于转轴标定方法，以实现多相机坐标系能高精度的统一在同一个世界坐标系之下(世界坐标系的z轴与转轴重合，xoy平面与圆柱异形标靶下端面重合)，从而实现对大型回转体全方位、高精度的测量。

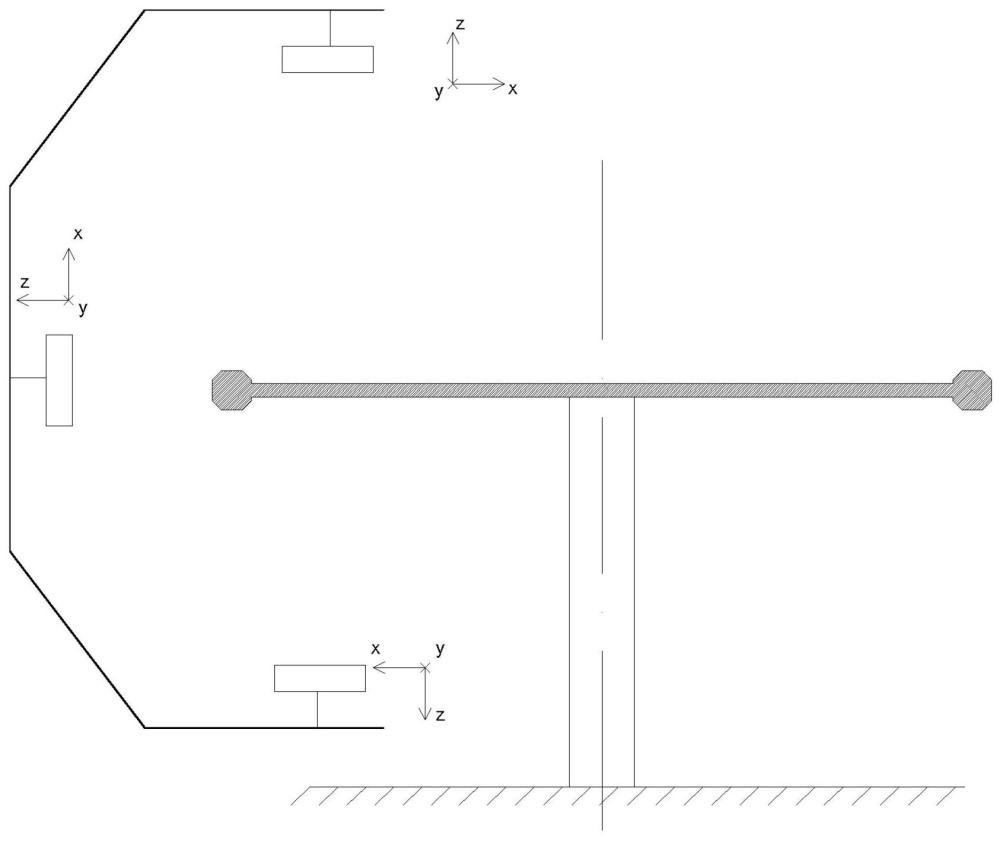
2、如图1所示，本发明中使用的测量系统采用了三台线激光传感器固定在一个c型架上，同时每台线激光传感器与c型架之间通过三个高精度的调整机构连接，可调节的量为各自相机坐标系y方向的平移以及x、z方向的旋转。转台在安装的过程中尽可能保证了转台台面的水平，故认为它的转轴处于竖直方向，并且转台上安装了编码器，对三相机实现数据同步采集创造条件。

3、本发明所述的方法如下：

4、步骤1：将多台线激光传感器的激光平面调整成共面并穿过转轴。

5、1.1)调节侧位相机激光平面穿过转轴。将水平泡放置在侧位相机表面，调节侧位相机控制z方向旋转的调整机构，使得侧位相机坐标系的xoz平面垂直水平面，然后同时调节x方向的旋转以及y方向的平移，使得侧位相机的激光平面以合适(需要保证上下位相机的激光平面也能在有限的调整范围内与侧位相机的激光平面重合)的角度穿过转轴。

6、1.2)调节上、下位相机激光平面与侧位相机激光平面重合。使用纸板水平放置在上、侧两相机激光共同可照射到的区域，调节上位相机控制z方向旋转的调整机构，使得在纸板上看见的两条激光线保持平行；接着将纸板竖直放置在上、侧两相机激光共同可照射到的区域，调节上位相机控制x方向旋转的调整机构，使得在纸板上看见的两条激光线保持平行；最后纸板不动，调节上位相机控制y方向平移的调整机构，使得两条激光线完全重合。移动纸板，在不同的位置查看两相机激光线重合情况，若仍然存在一定的间隙，重复本步骤直至满意。下位相机调整与上相机同理。

7、步骤2：使用多相机同步采集圆柱异形标靶数据。

8、将设计好的圆柱异形标靶水平放置在转台上，故圆柱异形标靶的转轴与转台转轴是平行的，其剖面图如图2所示，其整体高度为h，半径为r，边缘整体宽度为w。将三台相机设置为编码器触发采集模式，将分频数设置为n，每圈采集行数设置为m(m最好设置为偶数，具体原因在3.3)中进行说明)，启动转台同步触发三相机采集，最后输出图像并保存在本地。

9、步骤3：使用采集的圆柱异形标靶数据完成标定。

10、三台相机的标定原理类似，以上位相机的标定过程进行阐述。在设计的圆柱异形标靶中，只关心边缘区域提供的信息，所以需要对上位相机采集的每条数据进行筛选，将感兴趣的边缘数据提取出来。对m行数据中三段直线数据点分别使用ransac+最小二乘算法，去除异常点并拟合出三条直线段用于后续上位相机转换矩阵的求解。

11、3.1)求取上位相机y方向的旋转角度。求取m条拟合的中间直线段与水平方向的夹角αi(i＝1,2…,m)。圆柱异形标靶的转轴与转台转轴平行，αi(i＝1,2…,m)应该在一个标准值上下波动。使用ransac算法消除测量噪声带来的干扰，并根据一致性准则构建最小二乘问题，最小二乘表达式为

12、

13、根据(1)公式可以求出上位相机坐标系相对于世界坐标系在y轴方向的旋转角度α*，即：

14、令

15、

16、求出

17、

18、3.2)求取上位相机z方向的偏移量。在3.1)中已经求解出m条拟合的中间直线段与水平方向的夹角αi(i＝1,2…,m)，可以使用旋转矩阵(4)将左、中、右三条直线段整体旋转，使中间直线段变成水平状态。

19、

20、然后求取左、中直线段交点pil(xil,0,zil)以及右、中直线交点pir(xir,0,zir)，此时zil＝zir(i＝1,2,…,m)，因为圆柱异形标靶水平放置，故zil(i＝1,2,…,m)应该在一个标准值上下波动，需要将其求出。采用求取上位相机y方向的旋转角度同样的方式，使用ransac+最小二乘方法，求取：

21、

22、而上端面在世界坐标系下的z值是已知的，所以可以求出上位相机坐标系相对于世界坐标系在z方向的偏移量为

23、

24、3.3)求取上位相机x方向的偏移量。在实际安装过程中，圆柱异形标靶存在偏心放置，即其转轴与转台转轴并没有重合。这里对这种情况进行以下理论分析，当只考虑pil(i＝1,2,…,m)时，它所对应的真实轨迹在世界坐标系下是一个圆形。如图3所示，假设其圆心位于(-d,0),(d＜＜r)，对应的就是圆柱异形标靶的转轴与转台转轴距离为d，并假设其半径为r，所以圆的二维平面表达式为

25、(x+d)2+y2＝r2，  (7)

26、同时激光平面在圆面上投影的直线表达式为

27、

28、根据(7)、(8)公式可求得激光线被圆所截的长度为

29、

30、考虑一般情况，当圆心并不在x轴上时，圆心距离原点仍为d，则所截长度为

31、

32、根据(10)知道，lmax＝2r，现实中存在噪声以及数据采集过程中没办法采集到使得l取最大值的那个截面，所以对采集的数据点利用公式(10)进行拟合，已达到精确求解x方向偏移量的目的，具体做法如下：

33、创建一个新的变量xjl＝xjl+xj+m/2l,(j＝1,2,…,m/2)(保证能找到xjl(j＝1,2,…,m/2)对面的值xj+m/2l(j＝1,2,…,m/2)，这里将m设置为偶数)，然后构建目标优化函数

34、

35、式中，z为观测值上添加一个偏置。在真实情况下观测值xjl并非直接与模型测量值l对应，需要加上一个偏置才可以对应上。

36、针对(11)采用levenberg-marquardt求解，从而将d,z的数值进行求出。该算法对初始值的给出较为依赖，令：

37、

38、使用表达式(12)提供的初值将能保证更精确、更快速的求解出d,z，从而求出l'max，最终得出上位相机坐标系相对于世界坐标系在x方向的偏移量为

39、xoffset＝z/2，  (13)

40、至此，上位相机坐标系相对于世界坐标系的转换矩阵为

41、

42、使用同样的方法可以求出侧位相机坐标系以及下位相机坐标系相对于世界坐标系的转换矩阵。

43、本发明在硬件上采用独特结构设计的圆柱异形标靶，确保三台传感器能精确地拟合出特征点的空间位置；在算法上使用ransac、最小二乘和levenberg-marquardt算法，能有效抑制测量噪声的同时实现精确拟合和计算，这实现了三个测量坐标系相对于世界坐标系转换矩阵的精确求解。