基于改良高斯-马尔科夫模型的图像分割方法

本发明涉及计算机视觉和机器学习，特别是涉及一种基于改良高斯-马尔科夫模型的图像分割方法。

背景技术：

1、图像分割是图像分析和处理中最具挑战性的任务之一。因为图像经常被各种因素破坏，如噪声、强度不均匀性等。在过去的几十年中，基于不同的技术开发了许多图像分割方法。bouman,shapiro等人提出了一种直接解决无法计算精确的map估计值问题的贝叶斯图像分割的新方法。该方法性能更好，并且需要的计算量要少得多，其成果已发表在论文“amultiscale random field model for bayesian image segmentation”中。nikou,likas等人在2010年提出了一种新的贝叶斯模型，用于空间平滑度约束下基于高斯混合模型(gmm)的图像分割。数值实验证明了所提图像分割模型优于其他基于gmm的方法.其成果已发表在论文“abayesian framework for image segmentation with spatially varyingmixtures”中。steinberg，pizarro等人在2015年提出了用于图像聚类、图像片段聚类和无监督场景理解的新型分层贝叶斯模型。该模型在一些无监督模型与标准数据集上的监督和弱监督模型具有竞争力。其成果已发表在论文“hierarchical bayesian models forunsupervised scene understanding”中。

2、近年来，研究者们已经提出了几种基于混合模型和马尔可夫随机归档(mrf)的图像分割方法。hu c,fan w等人在2018年提出了使用空间平滑度约束进行建模，开发了一种变分贝叶斯学习方法来更新闭式表达式中的参数。通过涉及模拟和自然彩色图像的广泛实验，将所提方法的有效性与其他基于混合建模的图像分割方法进行比较。其成果已发表在论文“model-based segmentation ofimage data using spatially constrainedmixture models”。gu c,lu x,等人在2020提出了一种不需要估计模糊内核的新型图像去模糊方法。该方法在稳健性、视觉质量和定量指标方面优于最先进的技术。其成果已发表在论文“blur removal via blurred-noisy image pair”中。cheny等人在2021提出了一种用于图像分割的各向异性偏斜正态混合模型，与其他最先进的分割方法相比，该方法在合成图像和自然灰度图像上具有优越的性能。其成果已发表在论文“a spatially constrainedasymmetric gaussian mixture model for image segmentation”中。matteo giacomini,simona perotto等人在2022年提出了一种基于各向异性网格自适应程序增强的基于有限元的图像分割策略。该模型即使在存在高斯、斑点噪声的情况下也体现了准确性。其成果已发表在论文“anisotropic mesh adaptation for region-based segmentationaccounting for image spatial information”中。

3、然而在目前的研究中，图像分割仍是计算机视觉研究中的一个经典难题，对于存在干扰噪声的自然图像和自然艺术图像，其他高斯混合模型方法的图像分割应用效果仍有改进空间。而且马尔科夫链蒙特卡尔方法普遍存在的迭代收敛性问题。因此，本发明改进空间约束贝叶斯网络模型为图像分割技术提供了一种新的解决方法。

技术实现思路

1、发明目的：针对背景技术中指出的问题，本发明提出了一种基于改良高斯-马尔科夫模型的图像分割方法，通过结合空间变化有限混合模型(svfmm)和隐dirichlet分布(lda)进行模型初始化，创建了一个改进的空间约束贝叶斯网络模型，提高了图像分割的准确性和鲁棒性，该方法多个公开数据集上都展示了优于现有方法的性能，具有广泛的应用前景和显著的技术优势。

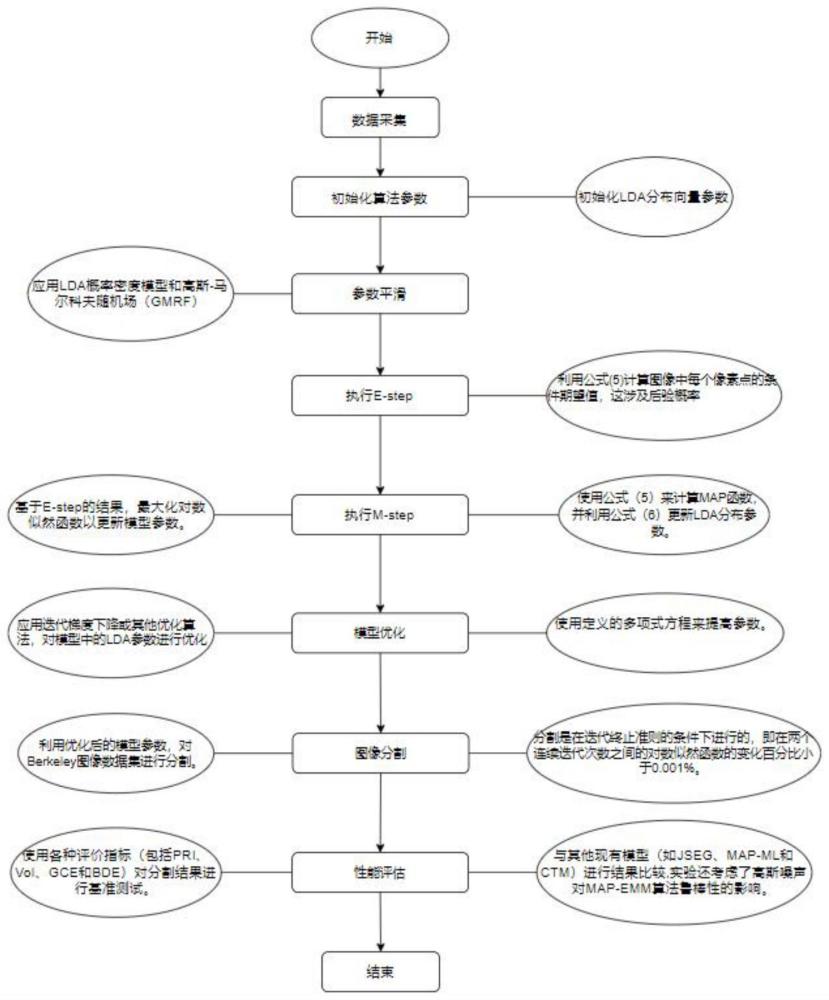
2、技术方案：本发明提出一种基于改良高斯-马尔科夫模型的图像分割方法，包括如下步骤：

3、步骤1：获取待分割图像，形成数据集；使用空间变化有限混合模型svfmm和隐dirichlet分布lda进行模型初始化；

4、步骤2：应用lda概率密度模型和高斯-马尔科夫定理的随机域参数混合过程，对模型参数进行平滑；

5、步骤3：计算图像中每个像素点的条件期望值；

6、步骤4：根据步骤3每个像素点的条件期望值，最大化对数似然函数以更新模型参数；

7、步骤5：应用优化算法，对模型中的lda参数进行优化；

8、步骤6：利用优化后的模型，对待分割图像数据集进行分割，得到分割结果。

9、进一步地，所述步骤1的具体方法为：

10、步骤1.1：选择输入图像数据集并确定模型参数，从数据集中选取输入图像数据集，同时确定模型的基本参数，所述基本参数包括高斯混合模型的组件数和lda的主题数；

11、步骤1.2：svfmm和lda模型初始化，结合空间变化有限混合模型svfmm和隐dirichlet分布lda进行模型的初始化，svfmm使用空间先验知识来保证像素的空间连续性，而lda则选用适当的先验分布并利用样本数据进行参数估计。

12、进一步地，所述步骤2的具体方法为：

13、步骤2.1：采用隐dirichlet分布(latent dirichlet allocation,lda)概率密度模型来描述图像的像素点和其对应的类别标签，lad分布的多项式形式用于描述像素点i属于第j个组件的概率，表示为具体公式如下：

14、

15、其中，是第i个像素点属于第j个组件的权重，k是组件或类别的总数，初始化包括设定主题数量、词汇大小以及先验分布；

16、步骤2.2：在lda模型的基础上，使用高斯-马尔科夫随机域(gauss-markov randomfield,gmrf)进行参数的空间平滑，通过以下先验概率分布来实现：

17、

18、其中，βj是第j个组件的平滑参数，n是像素点的总数，ni是第i个像素点的邻域，和分别是第i个和第m个像素点对应于第j个组件的权重；

19、步骤2.3：迭代梯度下降方法，根据高斯-马尔科夫随机域的先验概率分布，对模型参数α和β进行优化，在参数平滑和优化完成后，通过在小部分样本数据上进行快速的分割实验，验证平滑参数的有效性。

20、进一步地，所述步骤3的具体方法为：

21、步骤3.1：计算后验概率，在e-step中，首先，使用在步骤2中优化得到的模型参数，以及当前图像数据，来计算每一个像素点属于各个组件或类别的后验概率，通过以下公式来完成的：

22、

23、其中，是第i个像素点属于第j个组件的后验概率，是第i个像素点属于第j个组件的权重，k是组件或类别的总数；

24、步骤3.2：条件期望值计算；应用步骤3.1中的后验概率公式，对每一个像素点i，计算其条件期望值e[zi|xi；θ]，具体公式表示为：

25、

26、其中，xi是第i个像素点的观测数据或特征，z是隐变量z的某一个具体取值，p(z＝z|xi；θ)是条件概率，它表示在给定观测数据xi和模型参数θ的条件下，隐变量z取值为z的概率；

27、步骤3.3：更新隐变量；根据计算得到的条件期望值，更新图像中每个像素点对应的隐变量，将计算得到的每个像素点的条件期望值存储在一个矩阵中，以便后续使用。

28、进一步地，所述步骤4的具体方法为：

29、步骤4.1：定义优化目标；对数似然函数是模型参数和观测数据之间关联性的量化指标，使用以下公式来定义优化目标：

30、

31、其中，参数n、k、和ai等已在上述步骤中说明，代表第j个组件的概率密度函数，是空间平滑参数，是第i个像素点属于第j个组件的后验概率；

32、步骤4.2：基于优化目标和得到的条件期望值进行参数的更新，更新参数和参数具体的表达式如下：

33、

34、

35、在更新参数之后，需要检查模型是否已经收敛，如果对数似然函数的值或模型参数在连续几次迭代后没有显著变化，那么模型就认为已经收敛。

36、进一步地，所述步骤5中的优化算法为梯度下降、牛顿法和拟牛顿法中的一种。

37、进一步地，所述步骤5中的具体方法为：

38、步骤5.1：设定优化目标；优化目标是最大化对数似然函数；

39、步骤5.2：采用迭代梯度下降算法进行优化，进行lda参数的更新，迭代梯度下降算法将计算损失函数关于每个参数的梯度，并按照以下公式进行更新：

40、

41、

42、其中，η为学习率，是控制参数更新的步长；

43、步骤5.3：在每一次参数更新后，重新计算对数似然函数的值，以评估优化效果；如果函数值满足预定的停止准则，则优化过程停止。

44、进一步地，所述步骤6的具体方法为：

45、步骤6.1：数据集选择和预处理，选取待处理图像数据集作为分割对象，预处理包括图像的缩放、灰度转换；

46、步骤6.2：利用已优化的模型参数执行图像分割；

47、步骤6.3：分割算法执行完成后，将生成一个与原图像大小相同的标签图，其中每个像素点的标签表示该点属于哪一个分割区域或对象。

48、有益效果：

49、本发明通过引入改良的高斯-马尔科夫模型，显著提高了图像分割任务中的准确度和鲁棒性。该改进模型融合了隐dirichlet分布(lda)和高斯-马尔科夫定理的随机域参数，更贴近图像的实际分布特性，从而大幅提升了模型的实用价值和泛化能力。此外，本发明通过运用最大后验概率(map)和期望最大化(emm)算法，进一步优化了模型参数和分割效果。

50、在具体实施方面，本发明首先针对广泛应用的berkeley图像数据集进行了大规模的图像分割实验。接着，利用高级数学工具和数据科学库对图像数据进行了复杂的预处理和特征提取。在模型训练阶段，本发明详细描述了参数初始化、平滑、优化，以及性能评估等多个关键步骤，确保了模型能够在不同类型和复杂度的图像数据上都表现出色。

51、本发明不仅在图像分割准确度上表现优异，还通过参数平滑和优化步骤，增强了模型对噪声和不规则图像分布的适应性。更为重要的是，本发明对模型的实现过程进行了详细的分析和优化，不仅提高了模型的运行效率，还保证了其在大规模图像数据上的可扩展性。