含多孔隙的小模数粉末冶金齿轮啮合刚度预测方法

本发明属于齿轮传动，具体涉及一种含多孔隙的小模数粉末冶金齿轮啮合刚度预测方法。

背景技术：

1、小模数粉末冶金齿轮由于其高精度、高强度、低噪音、节能环保等优点广泛应用于汽车行业、军工制造业、电动工具、家电、玩具等领域。粉末冶金齿轮在压制成形与烧结过程中，不可避免的形成孔隙，占齿轮基体的6％～14％。由于孔隙的存在，会对齿轮的啮合刚度产生一定的影响。因此，探明含孔隙的小模数粉末冶金齿轮孔隙率与齿轮啮合刚度之间的关联规律，对后续研究小模数粉末冶金齿轮动力学特性，抑制齿轮的振动噪声具有一定的指导意义。

2、齿轮在啮合传动过程中会产生重要的动态激励，啮合刚度不仅是其重要的内部激励，也是齿轮动力学建模的重要参数之一，齿轮传动系统的工作性能与稳定性都与啮合刚度息息相关。通过高精度的时变啮合刚度计算，研究人员可以更好地了解齿轮系统故障机理、动态响应和固有特性。研究者们在齿轮啮合刚度求解方面已经做了很多工作，主要分为三种方法求解齿轮的啮合刚度：解析法、实验法和有限元法。

3、解析法采用较为复杂的公式建立齿轮的解析模型，数值解析法中基于weber-banaschek法的势能法则运用最广。解析法对于模型考虑的较为理想，虽求解速度较快，但局限性大，若实际模型较为复杂，解析法可能无法建模与求解。

4、随着测量技术以及实验设备的不断更新，学者利用实验法来测量出齿轮的啮合刚度，结果较为准确可靠。同时，实验法可以通过改变实验条件来研究不同因素对齿轮啮合刚度的影响，有利于深入了解齿轮啮合的机理。但是，实验法对设备和条件要求较高，需要专业的实验设备和技术人员进行操作，成本较高；并且，实验法只能测量特定条件下的齿轮啮合刚度，不能全面反映齿轮啮合的性能，需要结合其他测试方法进行综合评估。

5、随着计算机运行能力不断增强，基于数值分析的有限元法逐渐被用于求解齿轮啮合刚度。有限元法是一种基于数值计算的方法，相比于传统的试验方法，有限元法具有许多优点，并能模拟多种工况下齿轮的啮合情况。但是，现有技术多研究不含孔隙的齿轮时变啮合刚度，主要聚焦于齿轮的扭转刚度、齿根裂纹、点蚀、齿廓修形等对齿轮啮合刚度的影响。而粉末冶金齿轮成形过程中产生的孔隙会弱化齿轮的刚度，针对这些影响因素，少有研究其对齿轮啮合刚度的影响，且基于势能法的理论计算公式难以同时考虑孔隙对接触、弯曲、压缩、剪切与基体刚度的影响。

技术实现思路

1、本发明公开了一种含多孔隙的小模数粉末冶金齿轮啮合刚度预测方法，通过结合有限元接触分析，建立含孔隙的齿轮有限元接触模型，研究孔隙率对粉末冶金齿轮啮合刚度的影响规律，引入孔隙刚度修正系数对势能法进行修正，利用约束优化算法对修正系数进行求解，建立基于神经网络的刚度修正系数预测模型，对一定孔隙率范围内的时变啮合刚度进行预测，为粉末冶金齿轮的减振降噪设计提供理论支撑，从而可以有效解决背景技术中涉及的至少一个技术问题。

2、为实现上述目的，本发明的技术方案为：

3、一种含多孔隙的小模数粉末冶金齿轮啮合刚度预测方法，包括以下步骤：

4、步骤1，建立含多孔隙的小模数粉末冶金齿轮的有限元接触模型；

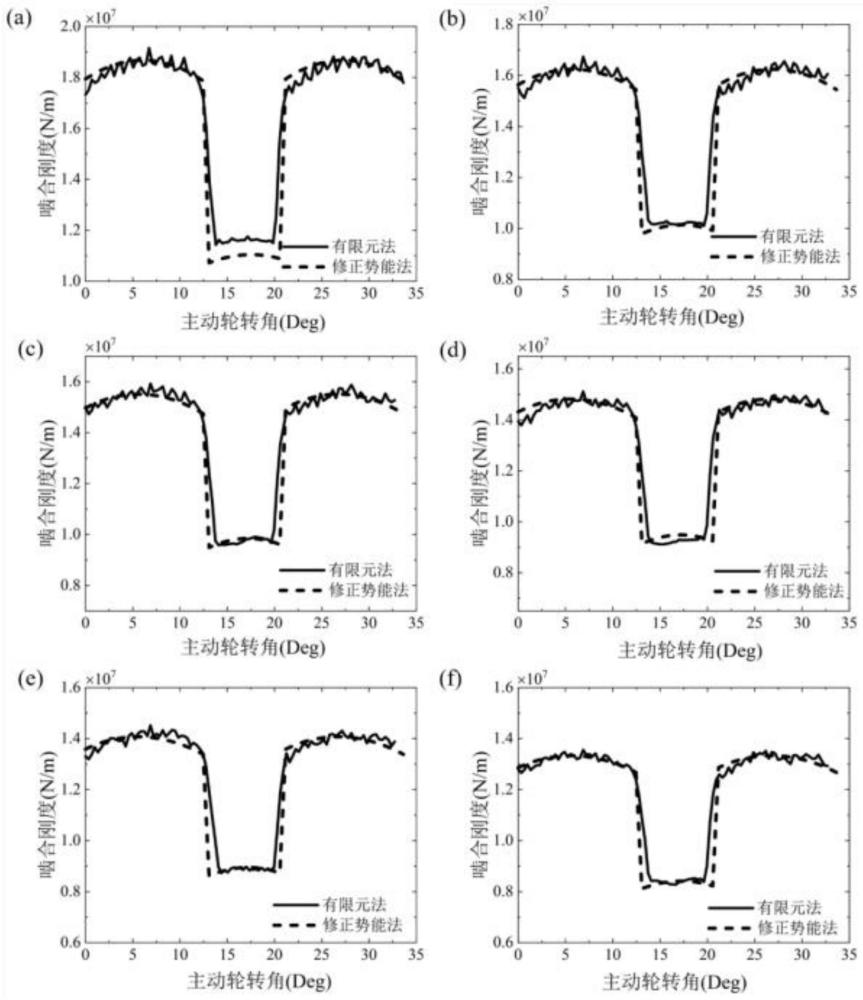
5、步骤2，求解有限元接触模型，计算齿轮时变啮合刚度，并与势能法进行对比，验证模型的合理性与可靠性；

6、步骤3，引入刚度修正系数，对势能法下的齿轮时变啮合刚度进行修正，建立含孔隙的刚度修正势能法公式，利用约束优化算法对刚度修正系数进行求解；

7、步骤4，建立基于前馈神经网络的刚度修正系数预测模型，对一定孔隙率范围内的时变啮合刚度进行预测。

8、作为本发明的一种优选改进，所述含多孔隙的小模数粉末冶金齿轮由铁基粉末冶金材料f-0000-20制备而成。

9、作为本发明的一种优选改进，所述有限元接触模型的参数为：齿轮模数m＝0.5mm，压力角α＝20o，小齿轮齿数z1＝17，大齿轮齿数z2＝31，小齿轮齿宽b1＝1mm，大齿轮齿宽b2＝1mm。

10、作为本发明的一种优选改进，所述建立含多孔隙的小模数粉末冶金齿轮的有限元接触模型，需将随机不规则孔隙设为规则网格单元的均匀缺失，具体包括：

11、将单齿模型拆分为利于控制网格尺寸的多个六面体并进行网格划分，基于有限元软件的二次开发，编制可删除有限元单元的脚本程序，实现按预设百分比删除有限元单元网格的功能，模拟粉末冶金齿轮的孔隙结构，再进行装配，形成考虑孔隙影响的粉末冶金齿轮的有限元接触模型。

12、作为本发明的一种优选改进，步骤2具体包括以下步骤：

13、在小齿轮和大齿轮的旋转轴线上分别设置刚体参考点，在参考点与轮齿内齿圈建立耦合约束，通过对参考点设置边界条件来控制齿轮的运动和受力；

14、利用有限元分析软件求解得到齿轮的角位移值，对数据进行处理得到啮合刚度曲线；

15、根据啮合刚度曲线，取稳定啮合时一个啮合周期内的啮合刚度与势能法进行对比，验证模型的合理性与可靠性。

16、作为本发明的一种优选改进，步骤三中，所述约束优化算法的表达式如下所示：

17、

18、其中，表示刚度修正势能法公式，kh为接触刚度，ka为压缩刚度，kb为弯曲刚度，ks为剪切刚度，kf为基体刚度，k为修正后的单齿啮合刚度，xh为接触刚度修正系数，xa为压缩刚度修正系数，xb为弯曲刚度修正系数，xs为剪切刚度修正系数，xf为基体刚度修正系数，λi为现有势能法基体刚度修正系数，rms表示对啮合周期内的刚度值取均方根值，ke为有限元法求得的啮合刚度值，lb表示解的下界，ub表示解的上界，x0表示解的初值。

19、作为本发明的一种优选改进，步骤4具体包括：

20、步骤41，建立样本集，将步骤3得到的刚度修正系数按均匀采样的方式，依照比例划分为训练集、验证集和测试集；

21、步骤42，模型训练，将孔隙率作为输入，不同孔隙率下的刚度修正系数作为训练目标，使用最小二乘目标函数结合共轭性和最陡下降法，求得前馈神经网络模型的最优参数，确定最小二乘目标函数的极小点，进一步建立孔隙率与刚度修正系数之间的非线性映射关系；

22、步骤43，模型应用，将经过上述训练得到的前馈神经网络模型应用到不同的孔隙率下，得到训练范围内任意孔隙率下的修正系数值，从而进一步得到任意孔隙率下小模数粉末冶金齿轮的时变啮合刚度。

23、本发明的有益效果如下：

24、1、本发明结合有限元接触分析，建立含孔隙齿轮的有限元接触模型，研究孔隙率对粉末冶金齿轮啮合刚度的影响规律，引入了孔隙刚度修正系数对势能法进行修正，并利用约束优化算法对修正系数进行求解，最后建立了基于神经网络的刚度修正系数预测模型，可以对一定孔隙率范围内的时变啮合刚度进行预测，从而为粉末冶金齿轮的减振降噪设计提供了理论支撑；

25、2、本发明发现了齿轮副啮合刚度变化量跟孔隙率变化量呈现出一定的线性关系，当孔隙率每增加2％时，齿轮啮合周期内的啮合刚度均方根值降低4.8％，该研究结果对齿轮传动系统的动力学分析以及降噪与延寿具有一定的指导意义。