一种图像中曲线结构追踪与重建模型及应用

本发明属于机器视觉，涉及一种图像中曲线结构追踪与重建模型及应用。通过使用基于一种深度端到端模型的有监督学习方式，对曲线结构进行追踪与重建。此项技术可以针对二维或三维图像中曲线结构目标进行追踪与重建，其重建结果质量达到同类技术中最优的性能。该项技术可以应用在遥感地图中的道路，眼底视网膜图像的血管，光学显微镜图像中的脑神经元等多种场景，具有极为广泛的实用价值。

背景技术：

1、曲线结构是一种线状、细长的对象，其强度与周围环境相比呈现变化。曲线结构的提取旨在从图像数据中定量识别这些对象，从而促进对分支连接和分布的统计分析。这在计算机视觉中是一个关键的研究领域，特别是对于医学图像中的神经元分支和血管，以及航拍图像中的道路。然而，尽管几十年的研究工作致力于自动化这一过程，但在遮挡和拓扑模糊的图像中提取曲线结构仍然是一项具有挑战性的任务。

2、曲线结构提取通常被看作是一个基于分割的问题。作为一种重要的分割工具，卷积神经网络能够自动从不同的图像中提取图像特征。然而，与典型的分割任务不同，曲线结构提取更加强调目标的连续性和连通性，而不仅仅是其轮廓。一些先前的研究已经将结构约束融入网络架构或损失函数中，以增强它们的有效性。然而，这些基于分割的方法仍然存在一个基本的挑战：即当面临两个相邻或交错的分支时，基于分割的方法往往倾向于错误地将它们识别为一个整体，导致会构成拓扑性的错误。

3、为了克服以上问题，基于重建的方法成为曲线结构的重要方向。基于重建的方法可以明确建模曲线的拓扑结构，并可以根据它们的重建过程分为两大类：基于全局优先的重建方法和基于局部优先的重建方法。

4、基于全局优先的重建方法作为分割方法的一种变体，从整体图像的角度提取节点或线段以生成骨架。这些自顶向下的方法，如图优化、骨架化和信号增强，可以通过将潜在边缘合并成网络来高效地提取弱枝干。然而，这些方法的一个主要缺点是由于噪声中的错误种子点，它们更有可能生成“虚假连接”。因此，需要进行后处理修剪算法或繁琐的人工修正才能生成最终的重建结果。

5、基于局部优先的重建方法往往从一个合理的种子点开始探索潜在的分支。作为一种保守的策略，这些方法优先考虑局部信息，并在图像信号变得模糊时停止执行，从而避免了虚假分支的错误。因此，局部优先方法成为解决大规模图像应用中的复杂拓扑挑战的一种有前途的方法，如神经元追踪或城市道路提取。然而，这些方法通常依赖于用手工设计的特征，如管状模板和射线模型。此外，局部优先方法还在很大程度上依赖于全局预分割掩模的准确性，以决定是否继续追踪，否则结果中可能会遗漏较多的弱枝干。

技术实现思路

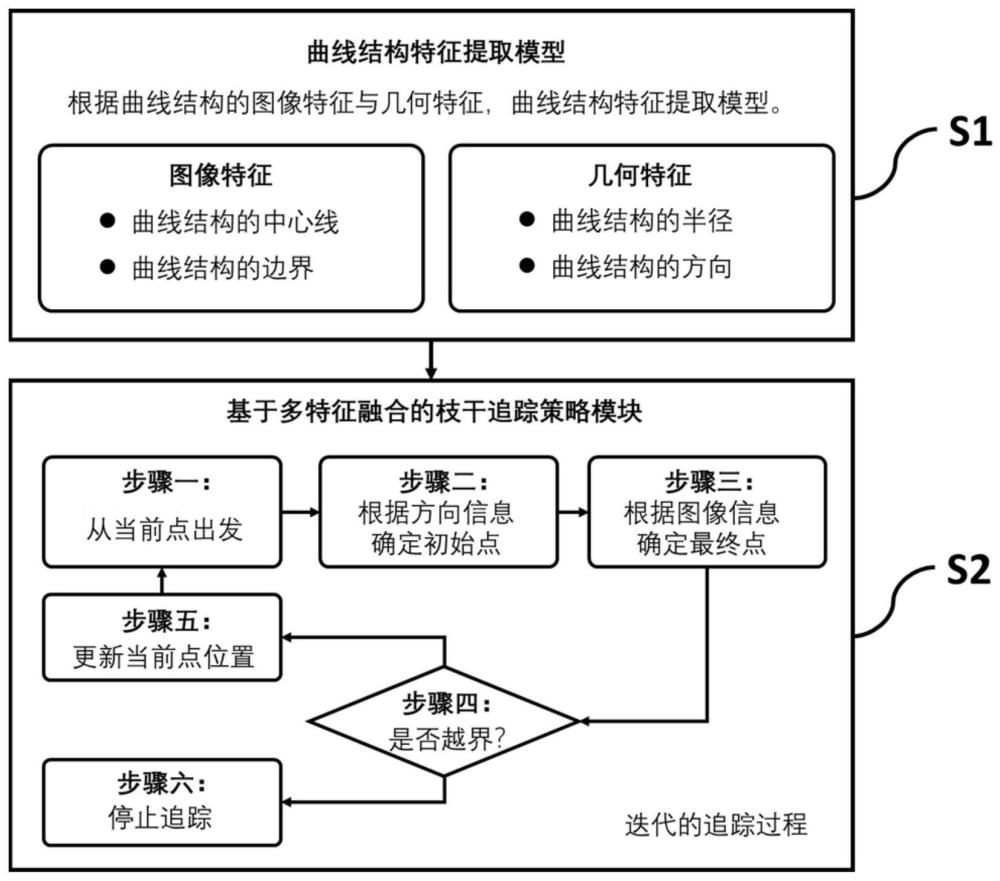
1、为了克服局部优先方法的上述局限性，本发明提出了一种图像中曲线结构追踪与重建模型，该模型包含两个模块，第一模块为曲线结构特征提取模型，通过设计一种u型深度网络模型，用于学习曲线结构的图像特征(中心线特征和边界特征)与几何特征(半径特征和方向特征)。第二模块为基于多特征融合的枝干追踪策略模块，用于将第一模块提取到的曲线结构特征的信息融合到追踪过程中，以迭代的方式完成整个枝干的重建。

2、为实现上述目的，本发明所设计的一种图像中曲线结构追踪与重建模型，包括的两个模块如下：

3、(1)曲线结构特征提取模型：为了自动的学习并提取曲线结构的特征，本发明设计了一种基于u型深度网络模型的曲线结构特征提取模型，其中包含四个子任务块，以便在集成的深度网络中同时学习外部图像特征和内部几何特征。对于外部图像特征，包含中心线提取模块，用于微调分支位置；边界提取模块，决定是否停止跟踪过程。对于内部几何特征，本发明设计了一种基于长短期神经网络的序列学习模块，分别用于方向估计模块和半径估计模块，以捕捉分支信号的光滑性和连续性，方向特征和半径特征用于确定迭代追踪的方向和步长。

4、(2)基于多特征融合的枝干追踪策略模块：基于上述曲线结构特征提取模型提取的图像特征和几何特征，从枝干上的一个种子点出发，采用迭代的方法探索整个曲线结构，完成最终的曲线结构追踪与重建任务。

5、优选的，所述步骤(1)构建曲线结构特征提取模型的具体内容为：

6、曲线结构可以表示为一个轴为三维空间中连续曲线的实体。这条曲线为点集对于每个点c∈c存在一个光滑函数{c(t)＝(x(t),y(t),z(t))t,t∈(a,b)}，其中c(t)是曲线结构的中心线。每个点的半径为r(t)，用于形成曲线结构的圆形横截面的。沿着中心线，可以将这些圆形横截面积分并以此拟合出图像i中的曲线结构s(t)。

7、为了便于计算，可将连续的中心线近似为m段线段，则曲线结构s(t)可以用离散的圆柱体si(t)表示：

8、

9、且每小段的曲线结构可以表示为：

10、

11、其中：

12、

13、其中，表示圆柱半径内的空间，其中d(ti)＝(v(ti),ζ(ti))是两个正交向量，它们与单位方向向量ξ(ti)一起构成了中心线的法平面，以上向量可以通过frenet架构公式获得。o(u)＝(cosu,sinu)t是圆的参数方程，其中u∈(0,2π]。

14、因此，准确的对曲线结构进行重建的问题可以看作是一个迭代追踪过程，具体可被分解为：估计位置点c(ti)、其半径r(ti)和方向ξ(ti)，以确定后续点c(ti+1)：

15、c(ti+1)＝c(ti)+r(ti)ξ(ti)

16、作为约束条件，所有的点c(ti)应该满足c(ti)∈s(t)的条件，以防止偏离中心线。最后，这个过程产生最终的实体s(t)作为重建结果。

17、曲线结构重建的优化目标为寻找合适的r*,ξ*和c*，其模型的损失函数为：

18、

19、其中，i[c(ti)]是中心点c(ti)处的图像，i[c(ti-l:i)]表示来自l个历史点的图像，yb和yc是图像的边界标签和中心线标签。表示与半径和方向估计相关的几何特征损失函数，而表示用于在跟踪过程中整合图像信息的图像特征损失函数。

20、为了估计上述曲线结构属性，本发明使用一种曲线结构特征提取模型，包含一个u型深度网络模型和四个子任务块提取图像特征和几何特征：中心线提取模块、边界提取模块，方向估计模块和半径估计模块。

21、曲线结构特征提取模型中的u型深度网络模型，包含三个主要组成部分：编码器、连接器和解码器。编码器采用4级瓶颈resblock实现，其输入为原始图像。连接器比原始u-net模型具有更宽的底层网络，这种配置允许网络提取更全面的高级语义信息，可以表示为连接器的输出同时作为方向和半径块的输入。解码器的架构与编码器类似，同样采用4级瓶颈resblock实现，目标是上采样编码特征以匹配输入图像的原始分辨率，可以表示为它的输出为中心线提取模块和边界提取模块的输入。

22、对于曲线结构的几何特征的学习，是指对连续枝干上的半径估计与方向估计的学习任务。考虑到连续枝干上的点往往与其相邻的点具有相似的方向和半径值。为了捕捉这一自然属性，模型将序列学习模块纳入半径估计模块和方向估计模块中，促进枝干平滑性和连续性的特征的学习。

23、在方向估计模块中采用lstm序列学习模型，其学习任务表示为方向估计模块由两个损失组成，即方向区间的分类损失和方向相似性的损失为确定方向向量的每个分量所属的方向区间，模型设计了方向估计的k类分类任务：

24、

25、其中j是向量分量的数量。具体来说，在3d空间中，j等于3，d(ti)包括沿x、y和z轴的向量的方向区间，表示为d(ti)＝[dx(ti),dy(ti),dz(ti)]；在2d空间中，j等于2，d(ti)包括沿x和y轴的向量的方向区间，表示为d(ti)＝[dx(ti),dy(ti)]。此外，为了获得精细的方向估计结果，模型引入了基于余弦相似性的方向相似性损失来计算两个方向向量之间的差别：

26、

27、对于每个向量分量

28、

29、其中k是类的数量，ak是每个方向区间的期望值。方向是通过取每个向量分量的方向区间输出的期望值来计算的。特别的，由于一个方向可以表示为数值相同但符号不同的正值ξ和负值-ξ向量，因此，当预测和真实向量之间的余弦相似度等于1或-1时，将为0，表示方向相似度更高。方向块的最终损失表示为：

30、

31、半径估计模块使用相同的序列学习模块，其学习任务表示为为了训练这个模块，采用了均方误差损失：

32、

33、将半径估计模块的损失函数和半径估计模块的损失函数结合起来，得到最终的几何损失

34、

35、其中λd和λr为平衡两个损失函数的权重。

36、对于曲线结构的图像特征的学习，分为图像的中心线提取模块和边界提取模块两个学习任务。中心线提取模块用于微调分支位置，边界提取模块用于决定是否停止跟踪过程。

37、中心线提取模块的目的是根据图像特征，在追踪过程中提供潜在的后继点。在此将中心线提取问题视为二进制分割任务。然而，曲线结构的中心线往往是细线形的目标，导致训练数据集中正面和负面数据的不平衡。为了解决这个问题，模型采用了加权的二进制交叉熵损失函数，该函数将更高的代价分配给前景枝干以提高性能。中心线损失的公式如下：

38、

39、其中yc[c(ti)]和表示中心线的真实值和概率图，wc是中心线前景的权重。特别的，将曲线结构上所有的点的半径r设置为1以生成中心线标签yc[c(ti)]。

40、边界提取模块决定是否在接下来的步骤中继续追踪。在这里同样将追踪决策视为边界分割任务：

41、

42、其中，是边界的概率图，wb是前景边界的权重。模型将所有的点的半径r设置为rb以生成边界标签。当rb的值较大时，追踪算法倾向于采用一种积极的策略；相反，当rb的值较小时，算法会变得更加保守。

43、因此，整体的图像特征损失函数可以定义如下：

44、

45、其中λc和λb为平衡两个损失函数的权重。

46、优选的，所述步骤(2)多特征融合的曲线结构追踪模型的具体内容为：

47、基于多特征融合的枝干追踪策略模块结合步骤(1)中提取的几何特征(包括方向和半径)和图像特征(包括中心线和边界)来迭代追踪分支。从种子点c(ti)开始，该模块分两步追踪分支。第一步，估计当前点的半径和方向找到一个初始后继点然而，由于图像质量低、模糊不清，的置信度通常很低。如果模型只遵循这个决策，就可能偏离中心线。因此，在第二步中，其目标是提高分支的准确性，引入中心线特征。这包括从潜在的后继点集q中识别离当前点最近的点作为最终决策：

48、

49、其中，tc是概率图的阈值。在中心线概率图中，显示值超过tc的点被包含在潜在后继点集q中。

50、此外，追踪过程中包含两种停止准则。第一个准则要求检查后继点的边界概率是否低于阈值tb。第二个标准是在后继点与先前追踪的区域重叠时触发的。

51、至此完成图像中曲线结构追踪与重建模型构建。

52、本发明的第二个目的是提供所述的曲线结构追踪与重建模型在各类包含曲线结构重建中的应用，例如卫星遥感地图道路提取，眼底视网膜血管重建，全脑神经元追踪与重建等2d或3d图像中的曲线结构重建任务，通过本发明的曲线结构重建模型，可以自动的完成上述各类曲线结构图像的追踪与重建。

53、所述的第一模块的曲线结构特征提取模型的应用，可分别针对2d和3d图像，提取图像中枝干的方向，半径，中心线和边界等信息。在网络训练时，需要预先产生对应的几何标签与图像标签，用于网络的有监督学习训练。在网络损失函数收敛后，完成网络的训练，可用于下一步的曲线结构的追踪任务。

54、所述的第二模块的基于多特征融合的枝干追踪策略模块，用于将第一模块提取到的曲线结构特征的信息融合到追踪过程中，从枝干上的一个种子点出发，以迭代的方式完成整个枝干的重建。

55、本发明是首个同时针对2d和3d图像中曲线结构的追踪与重建模型，具有模型配置简单灵活、重建结构质量高，应用范围广泛的优势，可用于曲线结构全自动重建任务，也可用于人工辅助的半自动重建任务，在各类图像重建任务中均获得更高的精确率和召回率，更好的枝干覆盖率以及更低的位置误差和半径误差，具有极大的实际应用潜力。